取勢、明道、優術
——對圖形面積一線等分問題的思考

胡柳青

(浙江省桐廬縣分水初中教育集團 311500)

章建躍博士提出了數學教育的“取勢、明道、優術”，意指教師要順應數學教改的潮流，懂得數學育人的原則，掌握提高數學教學質量的規律，提高教育教學能力，優化數學教學方法.在數學教育中，無論是概念的形成，定理、公式、結論的推導，還是過程、方法的探索都離不開解題教學，毫不夸張地講，“掌握數學就意味著善于解題”.綜觀當前數學解題教學，“教師示范講解，學生模仿練習”依舊是課堂的“主旋律”，“題海戰術” 依舊是應對考試的“法寶”.為何數學教育教學改革風起云涌，而數學解題教學卻還在“墨守成規”.我們不禁要思考：數學解題教學該如何“取勢、明道、優術”？下面是筆者在“圖形面積一線等分問題”解題教學中的一點嘗試，不當之處，歡迎廣大同仁斧正.

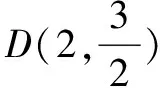
一、如何取勢

數學習題是由課本的有關知識、信息、符號，通過遷移、發散和綜合而來的，相關問題的知識源就是解決此類問題的最佳策略和致勝法寶.因此在解決具體問題時，我們首先要明確這是哪類問題，然后追溯與此類問題相關知識點有哪些，最后綜合條件選定解決本題所適用的知識點，因此，相關問題的知識源就是解決此類問題的突破口.圖形面積一線等分問題常見解決策略：1.過中心對稱圖形的對稱中心的任一條直線把它面積兩等分；2.三角形一邊上的中線把它分成面積相等的兩個三角形； 3.經過梯形上、下底中點的直線把梯形分成面積相等的兩個梯形； 4.直接運用圖形面積公式計算處理.由此，解題的方向即可明確.

二、如何明道

方向已經確定，接下來就應該是如何去解決問題，掌握解決問題的方法.教學中要以知識溯源為主線，以“怎樣做、怎么想、怎么拓”為三步曲進行專題復習，一題多解，多解歸一，讓學生知其然，然后知其所以然，從而起到事半功倍之效.

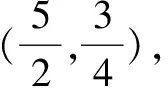
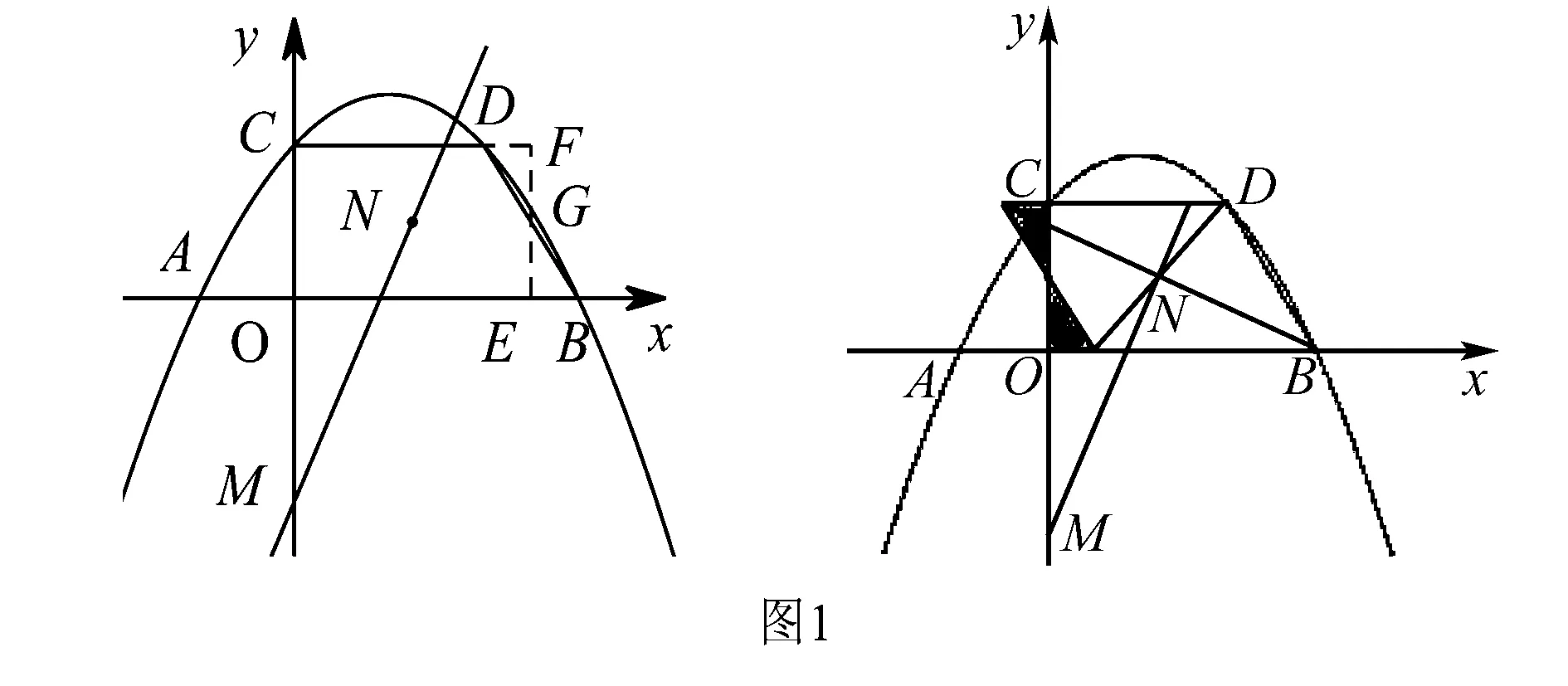
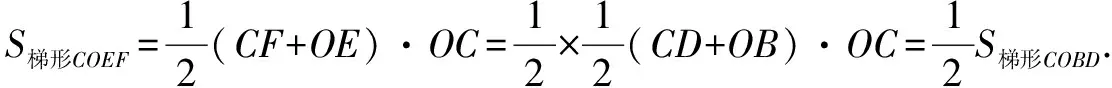
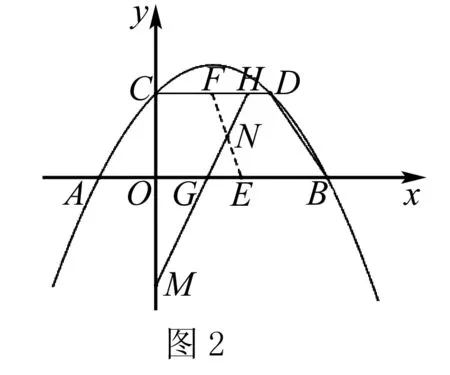
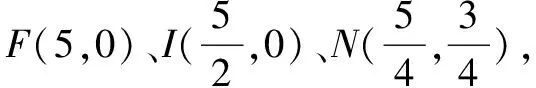
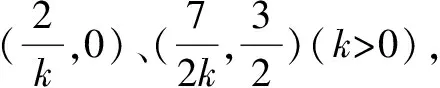
三、如何優術

“以題會類”的習題教學最高境界，是著重培養學生解決問題的綜合學力.通過上題的解析，為學生今后處理“圖形面積一線等分問題”提供了一個分析范本，極大地提升他們解決此類問題的能力.但解題不能只是目的，不能只為解題而解題，而要從解題中提煉出方法、思維，哪么，從上述的解題過程中我們還能有些什么思考呢？

思考一：解題的關鍵點在哪里，通法又是什么？

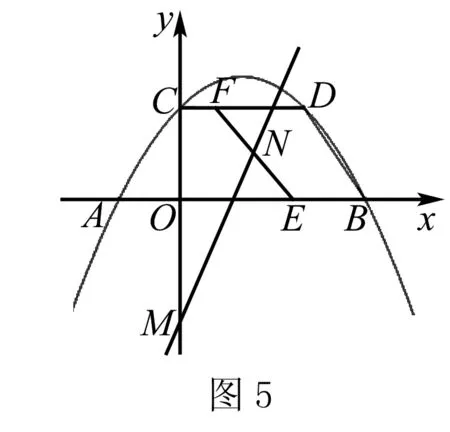
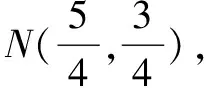
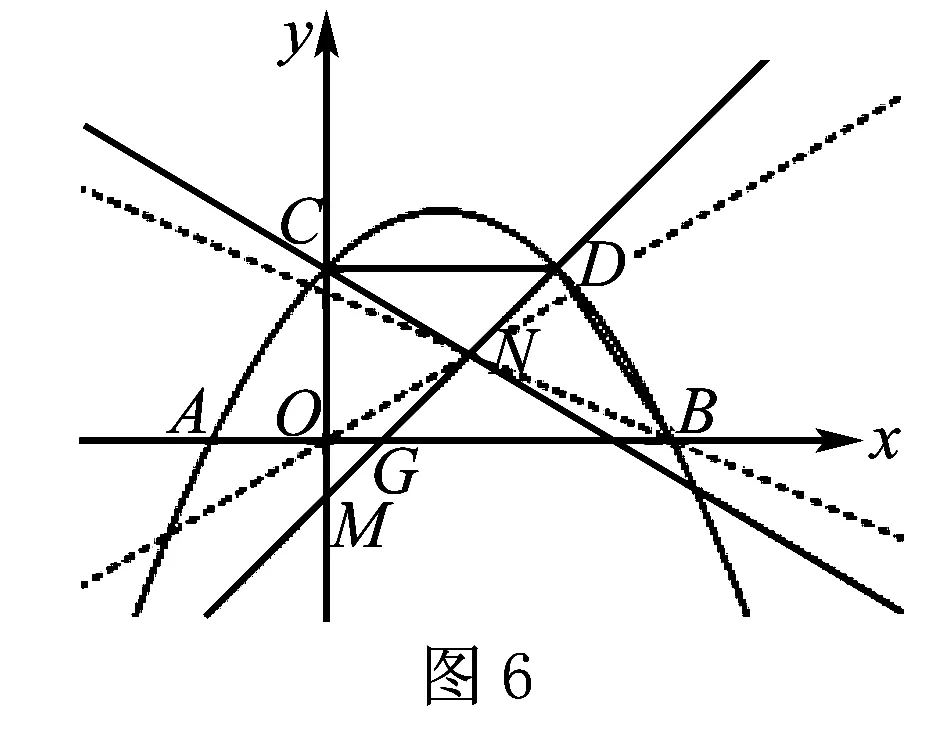
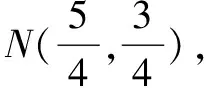
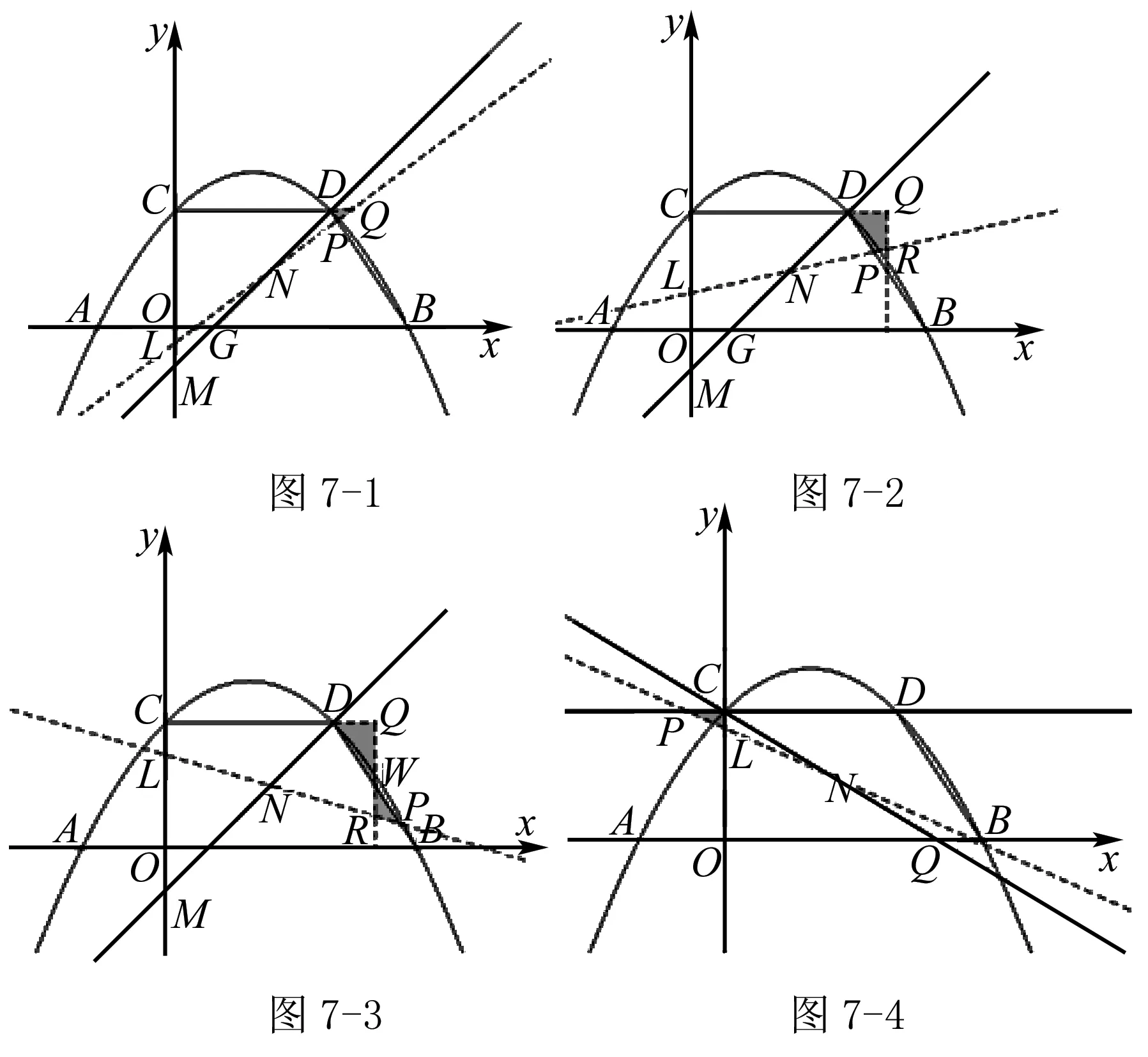
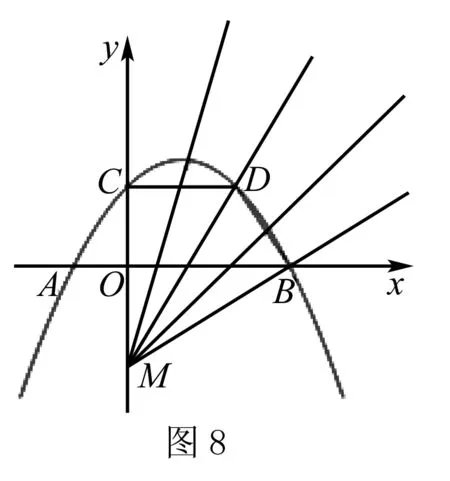
還可以繼續思考，在CM間是否存在某個點L，使得過LN的直線等分梯形OCDB的面積？如圖7-1，7-2，7-3，7-4，可得直線旋轉后所變化的圖形面積不可能為等積變化，由此可知點L不存在.同樣的，如圖8，如果點M不變，直線繞點M旋轉，則可得直線平分梯形面積的比值在不斷變化，也可得出直線的極限位置時，n的極端值，不再一一贅述.

思考三：三角形的面積如何等分，一般四邊形的面積又如何等分？解法3中利用三角形中線平分三角形的面積這一知識進行求解，繼續思考能否過直線外一點來平分三角形的面積？上述圖形是直角梯形，有一邊是平行的，為構造面積相等的三角形提供了便利，那么，如果是一般四邊形，又能如何平分.由此可得出下述求解方法.

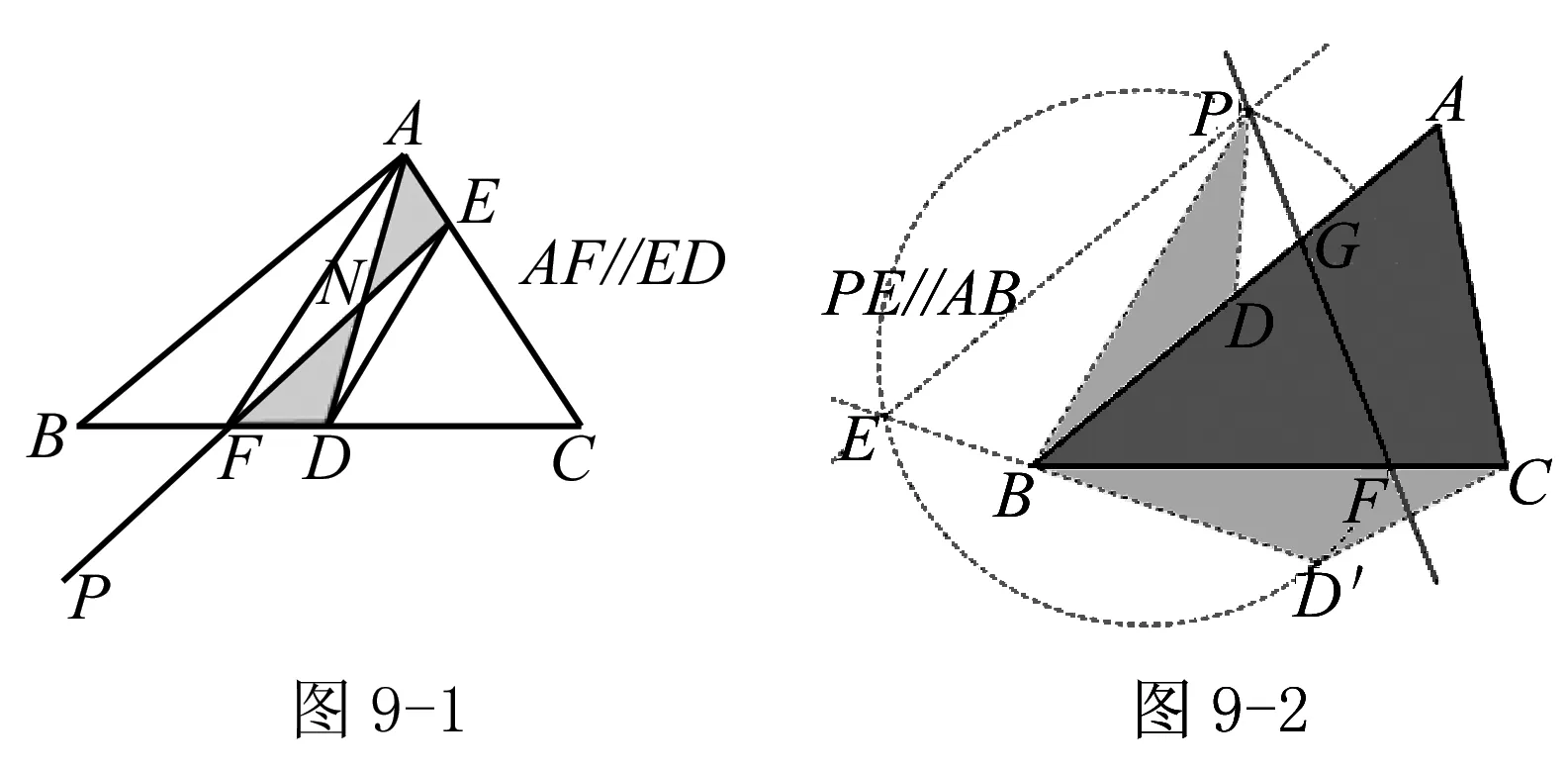
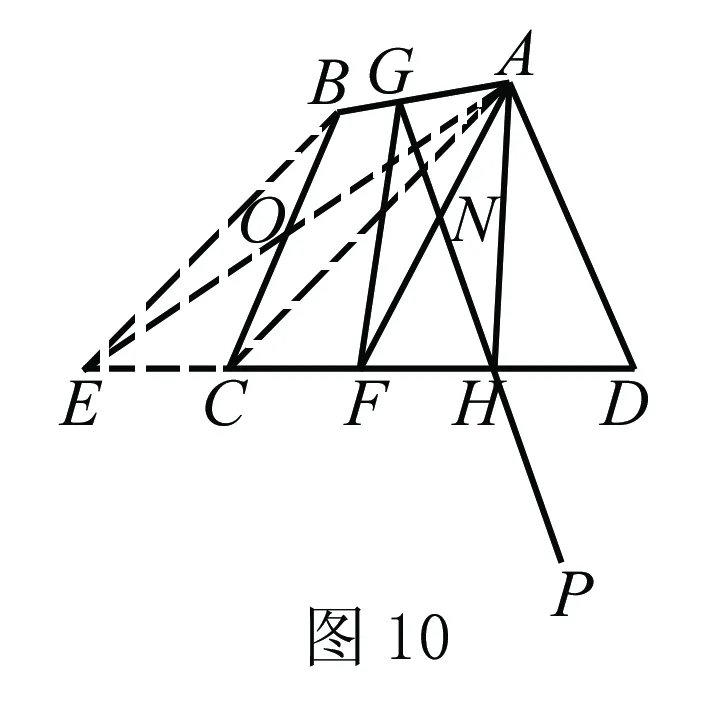
如圖10，聯結AC，過點B作AC的平行線BE，交DC的延長線于點E，連接AE，交BC于點O，則S△ABC=S△AEC，得S△AOB=S△COE．取DE的中點F，連接AF，得S△ADF=S△AEF．又S△AEF=S四邊形AOCF+S△COE=S四邊形AOCF+S△AOB=S四邊形ABCF，即S四邊形ABCF=S△ADF．故AF就是四邊形ABCD的面積等分線．過P作直線PN交AB、DC于點G，H，若GF∥AH，則S△AHG=S△AFH，可得S△AGN=S△FHN，由此可得直線PN等分四邊形ABCD.