基于灰色多項式回歸組合模型的維修器材需求預測方法研究

張 磊，于戰果，李世民

(1.陸軍邊海防學院， 西安 710108； 2.陸軍軍事交通學院， 天津 300161；3.中國人民解放軍63963部隊， 北京 100072)

一直以來，裝備維修器材的消耗需求預測都作為裝備保障的重要環節而倍受關注[1-4]，其基本過程是基于歷史數據，采用適當模型，進而推算其在下一階段所需的器材消耗數量[1-8]。對于輔助決策工作而言，具有極其重要的意義。

由于影響作用不同歷史時期的維修器材消耗量的因素很多，作用規律復雜且歷史數據有限[1-3,5-8]，因此大樣本需求量的模型并不適用。在這種情況下，灰色GM(1,1)模型得到了廣泛使用[1-3,5-8]。該模型非常適合用于處理具有“小樣本”、“貧信息”特點的不確定性復雜系統問題。

灰色GM(1,1)模型認為，系統內的數據積累和發展一般都存在能量的積累、存儲和釋放等過程，加之生成數列一般都有較強的指數變化趨勢，所以灰色系統理論指出，離散的隨機數經過累加生成變為隨機性被顯著削減的帶有指數變化規律的生成數列，進而運用指數形式函數構建預測模型。但是在維修器材預測的實際運用中，由于隨機因素的作用，數據列疊加后隨機特性消除并不徹底，造成實際數據圍繞預測曲線上下波動較大的情況[1-4]，這種“波動”可以通過擬合值和實際值之間的差值(殘差)來體現，因此很多研究通過運用各類模型針對不同歷史值的殘差進行分析，并推算下一階段的殘差作為修正值，對灰色GM(1,1)模型的預測結果進行修正，提高預測準確率。如運用Markov模型預測灰色GM(1,1)模型的殘差修正值[2-3]；運用BP神經網絡模型預測灰色GM(1,1)模型的殘差修正值[1]；運用傅里葉變換模型預測灰色GM(1,1)模型的殘差修正值等[5]。

然而，以上對于灰色GM(1,1)模型的運用僅僅適用于在序列累加后數據“大體上”呈指數函數規律變化的情況[7]。不適用于具有復雜函數形式規律的情形。為更加準確地反映數據列的變化規律，部分學者運用灰色線性回歸組合模型[8-9]體現并擬合出了指數函數規律和線性函數規律疊加序列的情形，取得了很好的效果。但是在隨機特性更加明顯的裝備維修器材需求變化序列中顯然不止這兩種規律，應該是更為復雜的函數形式。因此本文運用灰色多項式回歸組合模型深入挖掘數據列中除指數函數規律外的復雜變化規律，為各類基于灰色GM(1,1)模型殘差修正模型的廣泛應用奠定基礎。

由于灰色線性回歸模型[8-9]中通過序列累減的方式消除掉組合模型的線性函數項部分，運用求比值的方法消除指數函數的部分常系數以及變量部分，最后通過求對數值的方法確定指數函數的常系數。然而，這種方法對于數據列的要求較為苛刻，一旦累減序列出現負值時，便不能通過求對數的方法確定系數，而這種情況在實際預測時十分常見，顯然在運用灰色多項式回歸組合模型進行維修器材需求預測時不能夠運用這種方法確定系數。

本文運用函數的Taylor級數展開形式表示任意復雜函數并論證了灰色多項式回歸模型的合理性，通過推導給出了組合模型指數項系數的求解方法，最后運用最小二乘法確定灰色多項式回歸模型中的各項系數。

算例結果表明：該模型的擬合效果較傳統灰色GM(1,1)模型以及傳統灰色線性回歸模型有明顯提高，且隨著擬合采用項數增加，擬合精度也越高，證明了該模型的有效性和實用性。

1 灰色多項式回歸組合預測模型的建立

1.1 灰色GM(1,1)模型

灰色GM(1,1)模型是各類預測中經常用到的模型之一[7]，假設一維原始序列為{x(0)(k)}，k=1,2,…,n。其預測式可以表示為[7]

(1)

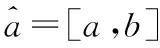
(2)

其中：

z(k)=[x(k)+x(k-1)]/2

其中，N為樣本個數。由(1)式確定的發展系數a反應了維修器材消耗量的發展態勢，若a< 0，則說明器材消耗數量的發展態勢是增長的，a的絕對值越大，增長越快；若a> 0，說明數據的態勢是減小的，a越大，減小越快。

1.2 灰色多項式回歸組合預測模型的形式[8-9]

由于方程式(1)的預測形式可以記為

其中：C1=x(0)(1)-b/a,C2=b/a,-a=v；可以看出，預測式(1)本質上為一個指數函數。

用線性回歸方程Y=aX+b及指數方程Y=aeX的和的形式來擬合疊加生成序列{x(1)(t)}，因此便得到灰色線性回歸組合模型的基本形式：

(3)

其中，C1、C2、C3和v均為模型的待定系數，由式(3)可以看出，灰色線性回歸組合模型可以很好地同時反映出疊加序列{x(1)(t)}中指數和線性的變化規律。

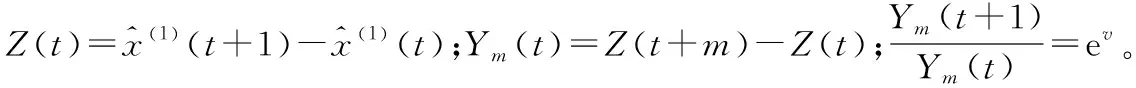
因此有：

(4)

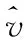
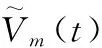
除單一指數函數規律和線性函數外，維修器材需求數據的變化往往體現出更為復雜的函數規律。假設除單一指數函數規律外，隨機序列一次累加后所體現出的復雜規律的函數為一個關于時間t的連續函數f(t)。用函數方程Y=f(X)及指數方程Y=aeX的和的形式來擬合疊加生成序列{x(1)(t)}：

(5)

同時，f(t)可以展開為其Taylor級數形式：

f(t)=f(t0)+f′(t0)(t-t0)+…+

其中，Rn(t)為Taylor級數的余項，是(t-t0)n的高階無窮小項，f(t0)及其在點t0處的各階導函數值f(n)(t0)(n=1,2,…)均可視為常數。在展開、化簡、合并同類項并忽略高階無窮小項后，函數f(t)可以近似表示為n階多項式的形式：

f(t)=C2+C3t+C4t2+…+Cn+2tn

因此灰色多項式回歸組合模型的形式(即式(5))可以表示為

(6)

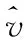
1.3 模型灰色發展系數的確定

這主要是由于函數(6)為變量t的連續函數，而式(6)所需要擬合的函數則是僅僅“大體上”呈現出式(6)變化規律的隨機離散值點，其隨機特性使得序列累減后求得級比值小于0的情況經常發生。因此，傳統灰色線性回歸組合模型中用于確定指數系數的方法并不適用于維修器材消耗需求的預測。

由1.2節的論述可以知道，灰色GM(1,1)模型的預測式可表示為

(7)

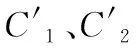
雖然式(6)和式(7)描述的為不同類型的曲線，但均是用于擬合同一組隨機離散點的近似曲線，兩曲線在相同時刻帶入擬合方程的點相同。也就是說，在理想狀況下，兩曲線重合，且均經過序列{x(1)(k)}上各點。在一般狀況下，兩類曲線的具體形式均是通過擬合隨機序列{x(1)(k)}的最小二乘法得到，兩曲線也是大致接近的，因此可以近似認為

(8)

對式(8)兩端求n+1階導可得：

化簡后可得：

(9)

因為式(9)左側應為常數，所以有：

v′=v

(10)

由式(10)可以知道，灰色多項式回歸模型的指數項的指數系數可以通過求解灰色GM(1,1)模型得到：

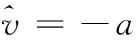
(11)

雖然將式(8)兩端求高階導可能產生較大誤差，但在模型實際使用中，受歷史數據量的限制，不可能使用項數較多的多項式擬合，因而避免了求高階導數而得到指數系數v的情形。

同時，雖然式(11)為近似得到，但a為序列的灰色發展系數，僅反應隨機序列的發展趨勢，并不影響組合模型的整體擬合精度。由此可知，v′可以視為灰色多項式回歸組合預測模型的灰色發展系數。

1.4 模型待定系數的確定

由于N為樣本個數，可以運用最小二乘法確定式(6)中的待定系數：

(12)

可以看出，當C4=C5=…=Cn+2=0時，式(6)退化為灰色線性回歸組合模型。當C3=C4=…=Cn+2=0時，式(6)退化為灰色GM(1,1)模型。由此，灰色多項式回歸組合模型解決了灰色序列指數規律和復雜函數規律疊加的問題。

在實際預測應用中，系數Cn(n=1,2,…,n+2)均起著修正擬合并提高精度的作用，均描述著隨機灰色作用因子對于時間序列作用[10]的結果。因此均可視為灰色作用量。

進行累減還原得到預測值：

(k=1,2,…,N)

(13)

1.5 殘差和相對誤差

(14)

在模型使用過程中，模型所使用擬合的項數越多，就越接近式(6)，取得的擬合相對誤差就會越小。但是在維修器材需求預測中，數據通常體現出小樣本的特點，因此擬合方程數量有限，不可能采用過多的項進行擬合。當擬合項數過多時，不僅會因擬合方程需求數量過多而降低擬合效果，甚至可能導致擬合多項式系數無法求解的情況。

2 實例分析

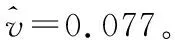
分別選取2項式模型、3項式模型和4項式模型擬合數據，三類模型可統一表示為

(15)

式(15)中當C5=C4=0時，式(15)為2項式模型(線性回歸組合模型)。C5=0時，式(15)為3項式模型。均不為0時，式(15)為4項式模型。由式(12) 、式(13)計算系數可得結果如表1所示。

表1 各類灰色多項式回歸模型系數

將表1中各階模型系數結果分別帶入式(15)計算擬合結果，由式(14)計算相對誤差，同時計算灰色GM(1,1)模型擬合結果，結果見表2。

表2 不同模型預測計算結果

由計算結果(表2)可以看到，灰色多項式回歸組合模型的擬合相對誤差較灰色GM(1,1)模型有了顯著的減小，且隨著擬合多項式項數的增加，擬合精度逐漸提高。特別是當擬合多項式為3項和4項式時，平均相對誤差由1.84%和1.79%降為0.85%和0.74%。說明灰色多項式回歸模型能夠更好地挖掘變化序列中的復雜函數形式變化規律，提高擬合精度。同時，隨著灰色多項式擬合項數的增加，運用最小二乘法擬合求解所需的數據量也就越多，但在實際運用時數據數量均是固定的，所以使用的擬合項數過多反而會影響擬合效果。本例中數據個數為8個，僅能提供8個擬合方程，當使用灰色8項回歸組合模型時將產生9個未知系數，則無法通過最小二乘法得到結果。

3 結論

1) 除單一指數函數規律外，灰色多項式回歸組合模型可以用于擬合隨機序列疊加后的任意復雜函數規律。

2) 在裝備維修器材需求預測問題中，灰色多項式回歸組合模型可以有效提高灰色GM(1,1)模型的預測精度，且采用灰色多項式擬合項數越多，擬合精度就越高。

3) 隨著采用灰色多項式擬合項數的增多，誤差修正的幅度也隨之減小，說明隨著時間t的次冪越高，該修正項對于整體預測值的修正效果越小。

4) 由于在維修器材實際預測中數據量有限，不宜采用過多的擬合項數，否則將影響擬合精度，甚至無法求解多項式系數。