基于建構主義的循環結構課堂教學設計

崔 玲，張榮茜，鄭小靜

（北京工業大學 信息學部，北京 100124）

0 引言

C 語言程序設計課程實踐性較強，是最能體現計算思維的一門課程，對于非計算機專業的學生來說有一定難度。語法點多、內容抽象，即使掌握了語法，學生在分析問題和解決問題時仍會感到無從下手，久而久之，一些同學喪失學習積極性，一些同學雖然很努力，但是因為初次接觸程序設計，顯得非常吃力。課堂教學如何引導學生快速接受程序設計理論，是一線教師著重思考的問題。

1 基于建構主義的教學方法

建構主義學習理論[1-2]強調要以學生為中心，在學習過程中充分發揮學生的主動性，能夠讓學生在原有知識和經驗的基礎上主動學習、構建新的知識。建構主義學習理論的主要教學方法有3種：支架式教學、拋錨式教學、隨機進入教學。

1.1 支架式教學

支架式教學指的是為學習者建構知識的概念框架，該思想來源于心理學家維果斯基的“最近發展區”理論[3-4]。維果斯基認為，學習者對于所要解決的問題和原有能力之間存在差異，這個差異就是“最近發展區”，而教育就是要消除這個差異，同時引導學習者進入更高水平的“最近發展區”。支架式教學主要由以下環節組成。

（1）搭建腳手架。圍繞知識點，按照“最近發展區”的要求建立概念框架。

（2）進入情境。將學生引入一定的問題情境。

（3）獨立探索。教師給予適時提示，讓學生獨立探索，在概念框架中不斷提升自己。

（4）協作學習。學生進行協商討論，在集體討論的基礎上完成對知識的意義建構。

（5）學習效果評價。對學習效果的自我評價和相互評價。

1.2 拋錨式教學

建構主義認為，學習者獲取知識應該主動去學習、體驗，而不是由教師傳授。該方法也被稱為案例教學，或者基于問題的教學。

拋錨式教學主要由以下環節組成：①創設情境。為學生提供與實際情況類似的問題情境。②確定問題。為學生選擇與當前學習主題相關的問題作為學習的主要內容。③自主學習。為學生提供求解問題線索，讓學生主動搜集信息、思考方案來解決問題。④協作學習。⑤學習效果評價。

1.3 隨機進入教學

對于復雜問題，學生可選擇不同途徑、不同方式進入同樣教學內容的學習，這就是“隨機進入教學”。隨機進入教學主要由以下環節組成：①呈現基本情境。②隨機進入學習。③思維發展訓練。教師提出的問題要有利于促進學生認知能力的發展，要有利于建立學生的思維模型。同時還可提出一些延伸問題培養學生發散性思維。④協作學習。⑤學習效果評價。

2 循環結構的課堂教學設計

在建構主義學習理論的指導下，結合程序設計課程的特點，進行課堂教學設計，引導學生在原有知識基礎上快速構建新知識。

2.1 設定問題引入知識點，激發學生學習興趣

學習循環之前，學生已經學會如何輸出1 行“Happy New Year！”，接下來讓學生思考：如何輸出10 行“Happy New Year！”？學生可能回答：復制、粘貼，那么可以再問：如果輸入1 000 行呢？

在給出對應的for 循環代碼之后，可以讓學生繼續思考：

如何輸出1 到10？

如何輸出1、3、5、7、9 的序列？

編寫程序驗證學生的想法，最后讓學生總結語句的執行順序，以及影響輸出結果的語句都有哪些。

通過以上實例，教師可以自然地引出for 循環的語法格式，并指出for 循環的四要素：循環變量初值、循環條件、循環變量變化規律和循環體。

再比如，講解例題“輸入n 個學生成績，計算平均分”之后，讓學生思考如何編程實現“輸入班級學生成績，計算平均分（其中班級人數未知，可用-1 表示輸入結束）”。學生根據已經學習過的for 語句可以編程實現，但是會發現循環條件與循環變量無關。此時教師可引出while 語句，并通過比較，分析for 語句和while 語句的相似和不同之處。最后進行總結：雖然for 語句、while 語句均可實現循環問題的求解，但由語法形式可知，for 語句更適合循環次數已知的問題，而while 語句則適合循環次數未知的問題。

2.2 漸進式教學，不斷推進學生的“最近發展區”

不僅例題講解要由淺入深，而且實踐練習也要由易到難，如掌握了for 語句的基本語法格式之后，教師可以設計與例題相似的題目，讓學生進行編程練習。

練習1：輸出A 到Z；

練習2：輸出AaBb……Zz；

練習3：輸出100 到1 000 之間的偶數。

對于練習1，可以提示學生，利用已學知識解決問題：①字符類型可以參與算術運算，如ch=ch+1；②語法中未規定循環變量必須是整型。

練習2 有一定難度，雖然與練習1 相似，但是多數學生無法一下總結出AaBb……Zz 的規律。此時教師可以提醒：在已學過的分支語句中，執行的語句可以是復合語句，那么循環語句中的循環體也可以是復合語句，將Aa、Bb、Cc 視為一組即可找到規律：

練習3 難度再次增加，循環體是分支語句，這是循環語句與分支語句的簡單混合應用。

再比如，循環嵌套是學習的一個難點，通過對已有案例的升級改造，可以讓學生在已有知識基礎上，輕松接受循環嵌套。

案例1：已知如何輸出1 到10，思考如何輸出10 行的1 到10。

由該案例引出雙重循環，此處要重點分析內層循環變量和外層循環變量的變化規律。同時可讓學生練習如何輸出九九乘法表、三角圖形等。

案例2：已知如何計算n！，思考如何計算1+2!+3!+…+n!。

在該案例中，要著重注意變量初值及其所在位置問題。存儲求和結果的變量初值應為0，放在外層循環之前。內層循環用于求階乘，那么存儲求階乘的結果，初值為1，應放在內層循環之前外層循環之內。素數問題是循環結構的典型問題，也是枚舉算法的一個典型應用。在講解素數問題之后，可給出以下兩個案例，繼續學習循環的嵌套用法，也可讓學生進一步了解枚舉算法的基本思想。

案例3：已知如何判斷一個數是否是素數，思考如何輸出100 到1 000 之間的素數。

案例4：通過講解雞兔同籠問題，讓學生練習百錢買百雞、搬磚等問題。同時，還可讓學生思考有無多種解法，如雞兔同籠問題的常規解法是二重循環，思考是否可用一重循環解決。

2.3 啟發式教學，調動學生學習主動性

素數問題對于非計算機專業的學生來說，問題簡單，但實現時容易出錯。關鍵點在于什么時候給出判定結果，很多同學往往在循環中直接給出判定結果，如：

教師在講解時不用立即否定學生想法，可運行程序進行測試，通過運行結果學生會逐漸意識到問題所在。這時教師和學生再一起思考解決方法，在這樣不斷嘗試不斷修改的過程中逐步理清思路，達到求解問題的目的。這個過程會讓學生有種成就感。

同一問題往往有多種解法，在練習素數問題時，會有不少學生的解法思路都很巧妙。教師可讓學生展示給大家，然后一起分析其優劣。

方法一：

該方法定義了變量flag，表示能整除n 的個數，循環結束后，如果flag 為零，表示n 為素數，否則n 不是素數。

容易理解大于n/2 的數不會整除n，程序中循環條件為i＜n/2，比i＜n 減少了循環次數，提高了運行效率。

方法二：

方法二較方法一有3 點變化：①變量flag 的含義。flag 為1 表示n 是素數，flag 為0 表示n不是素數。這種變量稱為邏輯型變量，常用于邏輯判斷問題，一般取值為1 或0，表示是或否、真或假。②可以證明，一個素數的兩個因數，至少有一個小于等于根號n。sqrt（n）是判斷素數的最小臨界條件。因此該方法中循環條件是i＜=sqrt（n），進一步減少了循環次數。③break的應用。只要某個i 可以整除n，則執行break，跳出循環，再次減少循環次數。對于復雜程序來說，減少循環次數會極大提高程序運行效率，教師可以借此向學生介紹一下算法復雜度問題，讓學生認識到算法在程序設計中的重要性。

方法三：

該程序非常簡練，但不易理解，該程序思路可由方法二推出。方法二中使用了break 語句，如果滿足n%i==0，則結束循環，也就是說n%i!=0 是循環條件之一。因此循環條件是n%i!=0&&i＜=sqrt（n），循環結束表示這兩個條件至少有一個不滿足。如果不滿足n%i!=0，表示存在一個數可以整除n，則n 不是素數。

2.4 支架式教學，幫助學生輕松構建知識框架

2.4.1 將應用問題分類，提高學生求解問題能力

編程的難點不在于語法格式，而是如何將實際問題的求解方法轉化為符合語法格式的程序語句。教師可以將應用問題進行分類，為學生求解問題提供思路，幫助學生逐步提高利用程序求解問題的能力。一般來說，可用循環結構解決的應用問題有如下幾種：①有規律輸出問題，如輸出Fibonacci 序列。②累加累乘問題，如求n！。③連續輸入并進行計算的問題，如輸入班級學生成績并求平均分、最高分。④枚舉問題，如素數、雞兔同籠問題。

每類問題可講解1～2 個案例，然后讓學生獨立求解類似問題加以練習。也可對案例進行改編，如將問題：“根據公式，計算前n 項之和，求解π 的近似值”，改編為“根據公式，求解π 的近似值，直到最后一項的絕對值小于10-6”。

2.4.2 將求解步驟模式化，重復訓練，培養學生計算思維能力

思維能力的培養離不開大量重復的訓練。對每一個案例，均按照“問題描述、問題分析、算法描述、程序實現、運行結果、程序分析”6 個步驟[5]，進行問題求解，逐步引導學生掌握程序設計的基本方法，培養學生計算思維能力。

以位數分解問題為例。

（1）問題描述。

輸出1 至10 000 之間每位數的乘積小于每位數的和的數。

（2）問題分析。

類似解數學題，首先分析題意。該題最終要求輸出一些數，這些數的范圍是1 到10 000。由此可知輸出是一個循環，循環范圍是1 到10 000。該部分算法可描述如下：

再分析，輸出的數是要滿足一定條件的，即每位數的乘積小于每位數的和。算法修改如下：

最后分析如何求和、求乘積，題目要求的是i 的每位數的乘積與每位數的和。因此要求和與積，首先要分解i，得到它的每個位數。

如何分解一個數呢？在學習算術運算時，已經學過如何分解位數確定的數，如i 是三位數，則i%10 即個位數，（i/10）%10 即十位數，（i/100）%10 即百位數。但是該題目中位數可能是1、2、3、4、5，該如何分解出它的每位數呢？分解操作何時結束呢？我們只能嘗試尋找有無規律可循。先用實際的數進行嘗試，然后試著總結規律，見表1。

通過實例分析可知，分解位數可由循環實現，重復的操作是：

什么時候停止重復操作？當m 為0 時。

分解位數的目的是求其和與積，因此在分解的同時計算和與積。該部分算法描述如下：

表1 分解位數實例分析

（1）算法描述。

根據問題分析，求解問題的完整算法如下：

（2）程序實現。

類似中英文翻譯，將算法轉換為C 語言代碼。

（3）程序分析。

該例的難點在于如何分解一個不確定位數的數。已知確定位數的分解方法，那么可以嘗試總結不定位數的求法是否與之有相同之處。容易知道，個位數為m%10，十位數對于m/10 來說也是個位數，百位數對于（m/10）/10 也是個位數，因此可以把問題歸結為求個位數，問題就變得簡單且有規律，通過幾個實例分析可得出求解規律。

另外要注意，該例程序中的m=i，為什么不直接用i 呢？原因在于m 是變化的，最終的m 會為0，而i 則是要輸出的數，而且i 是外層循環的循環變量，不能輕易改變。初學者容易犯的錯誤就是在循環中不小心改變了循環變量的值，而這種錯誤屬于邏輯錯誤，難于察覺，很難找到錯誤所在。由此還可以給學生介紹一些調試程序的方法，比如在可疑語句前后加入輸出語句查看變量變化，或者直接使用編譯軟件提供的調試工具。

2.5 對比式教學，深入理解知識點，培養學生思辨能力

do-while 語句較為簡單，可對比while 語句學習。與while 語句不同，do-while 語句是至少執行一次循環體，而while 語句則可能一次都不執行。

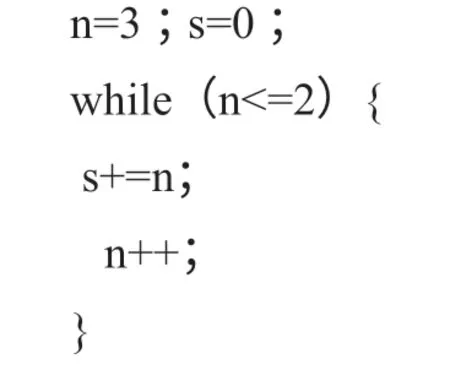
上述程序段中while 循環條件不滿足，不會進入循環，執行之后，s=0，n=3。而下面程序段中do-while 語句會先執行一次循環體，再退出循環，執行之后，s=3，n=4。

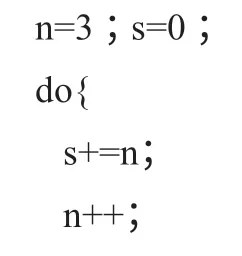
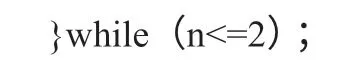
同樣，可以對比學習break 和continue。在循環中，break 是結束循環，類似于游戲中的“Game over！”；continue 是結束本次循環，類似于游戲中的“Try again！”。

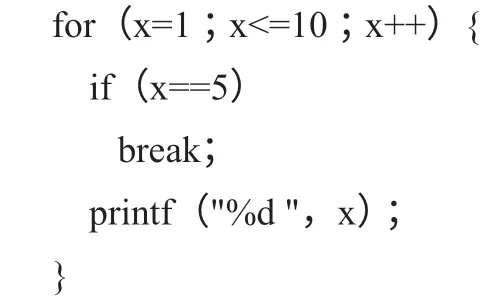
上述程序段輸出1、2、3、4，隨后跳出循環。而下面的程序則會進入死循環，因為x 會一直停留在5，循環條件一直未能打破。

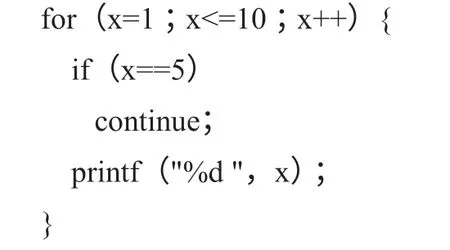
2.6 機房授課，邊講邊練，強化學生實踐能力

對于實踐性較強的課程來說，課堂教學安排在教室上課，非常不利于學生實踐能力的培養。我校從2010 年開始，將C 語言程序設計等計算機公共基礎課程安排在機房上課，授課模式由講練分離變為邊講邊練，在學習一個知識點之后即刻讓學生進行練習。由近幾年的教學評價來看，這種模式有助于激發學生學習興趣，培養學生實踐能力，提高教學效果。

3 結語

循環結構是C 語言程序設計的重點和難點內容，基于建構主義的教學方法可以讓學生在原有知識基礎上，由易到難、由淺入深逐步引導學生主動去分析問題、解決問題。多年教學實踐證明，該方法有助于培養學生的計算思維能力，有助于激發學生的學習興趣，培養學生的自主學習能力。