一道線性回歸方程的變式與應用

■何海虹

同學們在做題時，不要一味地追求題海戰術，而應注意典型習題的挖掘，特別是一些優秀的高考題，將它們轉化成一些相關的變式題，這樣可使大家在試題的變換中，尋求“以不變應萬變”的解題方法，從而達到舉一反三的目的。

題目根據表1中的樣本數據，得到的兩個變量y與x之間的回歸方程為?y=b x+a，則（ ）。

表1

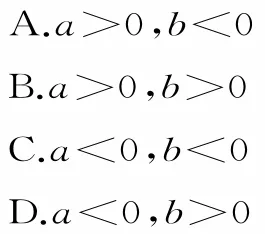
由題意作出散點圖，如圖1所示，觀察圖像不難得出，回歸方程?y=b x+a的斜率b＜0，當x=0時，截距a＞0，所以a＞0，b＜0。故選A。

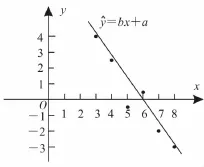
解答此類問題的關鍵是先畫出散點圖，再根據散點圖中回歸方程的斜率、截距來判斷系數b，a與0的大小關系。

分析：結合上題中對應的樣本數據，通過合適的拓展即可得到如下的一些變式及其應用。

變式1：根據表2中的樣本數據，可知兩個變量y與x之間的回歸方程?y=b x+a必過點____。

表2

變式2：根據表3中的樣本數據，可知兩個變量y與x之間的回歸方程可能為（ ）。

表3

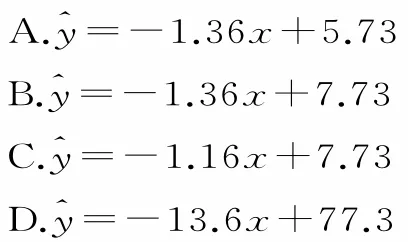
變式3：根據表4中的樣本數據，得到兩個變量y與x之間的回歸方程為?y=—1.36x+a，則a的值為____。

表4

變式4：根據表5中的樣本數據，得到兩個變量y與x之間的回歸方程為—1.36x+7.73，則t的值為____。

表5

變式5：根據表6中的樣本數據，可知兩個變量y與x之間的回歸方程中，變量x增加1個單位時（ ）。

表6

先根據題目數據確定對應的回歸方程?y=b x+a，再結合回歸方程中對應參數的性質來確定變量的變化情況，從而得以正確解題。

變式6：根據表7中的樣本數據，得到兩個變量y與x之間的回歸方程為?y=b x+a。

表7

（2）試預測當x=10時，對應的y的值。

解答本題的關鍵是正確求出回歸方程，理解回歸方程中相應參數的實際意義，并能加以靈活應用。