淺談點差法在高中數學中的應用
湯伊靜
(浙江省杭州市學軍中學 310000)
一、點差法解答圓錐曲線基本原理


二、點差法的基本應用
與弦中點相關的問題有三種:平行弦的中點軌跡;過定點的弦的中點軌跡;過定點且被定點平分的弦所在直線方程.其他問題都是由這三類問題衍生出來的.
1.已知弦中點求弦所在直線方程


解設弦是AB,由點差法的小結論可知:


由此可見,具有斜率的弦中點問題,常常用點差法作答,設而不求,消去多個參數,得出最終答案.注意,如果是曲線的存在性問題,判斷點M的位置至關重要,如果點M在曲線外,中點弦將不存在.
2.巧用點差法解對稱點題型
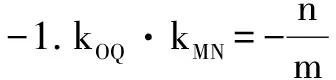

解當直線AB斜率不存在時且與橢圓C相切時,M在x軸上,故滿足條件的直線有兩條.



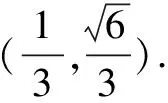
點評此題看上去偏難偏怪,初看題讓人無從下手,不知道怎么對“滿足M為線段AB中點的直線l有4條”的條件下手,但只要抓住中點在橢圓內,一定會有4條直線,可以快速求得范圍.
3.運用點差法證明定值存在性問題
此類問題中,一般是已知中點,運用點差法證明問題,同樣的,設點坐標,寫出兩定點過直線的方程,相加減即可得出答案.同時,如果是二次曲線與直線相交,韋達定理也為我們提供解題的途徑.
以2018年高考數學題為例:

如圖,已知點P是y軸左側(不含y軸)一點,拋物線C:y2=4x上存在不同的兩點A、B滿足PA、PB的中點均在C上.設AB的中點為M,證明:PM垂直于y軸.


4.利用點差法求解取值范圍
在高中數學中,求取值范圍都是熱門考點,一般題目設直線方程即可求解,但遇到兩種二次曲線共存的題目或是有n個交點的題目,設直線方程的方法就很繁瑣,此時,設點坐標求解較為便捷,同時注意中點的構造.


若任意以點A(0,1)為圓心的圓與橢圓至多有3個公共點,求橢圓離心率的取值范圍.
此題有一個陷阱:許多學生會想當然的把圓與橢圓交于(0,1),(0,-1)的點當做臨界條件,但這么做是不對的.運用“正難則反”的思想,最多有3個公共點等同于求4個公共點范圍.

點評此題運用設直線方程法也能求解,但是比較慢,容易出現計算錯誤,此處自己構造中點,熟練運用基本數學思想,大大簡化的計算步驟,提高了正確率.
5.點差法與其他方法的聯系
在點差法的記憶中,筆者發現它與隱函數求導有著千絲萬縷的聯系,對圓錐曲線進行求導,代入x0,y0(x0,y0為中點),把y′換成k,可以得到點差法的式子.下面給出隱函數求導過程:

由此可見,雖然隱函數求的是切線的斜率,點差法求的是中點弦的斜率,但仍有較大相似處.其中,隱函數求導的方法,在計算二次曲線與直線相切的題目中有著廣泛應用.
綜上所述,點差法在各式各樣的題目中均有較大應用,同時作為一種基礎數學方法,它與其它數學方法之間有著極大的相關性,這是我們在解題過程中所不能忽視的,要學會融會貫通,舉一反三,在學習點差法的解題技巧過程中熟練掌握運用其它方法,高中數學學習才能達到事半功倍的效果.

