例談函數單調性的“四用”
劉依軒
(河北省唐山市第二中學 063000)
函數單調性是函數的重要性質之一,也是高考熱點問題之一,我在學習中不斷地總結了函數單調性的一些問題,下面舉例說明函數單調性在解題中的應用.
一、正用
是指直接利用單調函數概念,證明或判斷一個函數是增函數或減函數.其步驟通常是:(1)設x1,x2是給定區間內的任意兩個值,且x1 證明如下:任取x1,x2∈(1,+∞),且x1 ∴f(x1)-f(x2)>0,即f(x1)>f(x2). ∴f(x)在區間(1,+∞)上是單調減函數. 同理可證,f(x)在區間(-∞,-1)和(-1,0)以及(0,1)上的單調性. 點評由定義法求函數的單調區間時,需要分兩步:一是在定義域區間內設兩個數x1 例2 已知函數f(x)=x2-2ax+3a2-1 (a>0,0≤x≤1). 分析將f(x)=x2-2ax+3a2-1配方得f(x)=(x-a)2+2a2-1,有同學認為f(x)的最小值是2a2-1,最大值不存在,這是錯誤的.根據函數對稱軸與定義域的關系,需要討論直線x=a相對于區間[0,1]的各種可能. 解(1)f(x)=x2-2ax+3a2-1= (x-a)2+2a2-1.當a≥1時,由于f(x)在[0,1]上是減函數,故f(x)的最大值為f(0)=3a2-1,最小值為f(1)=3a2-2a; 當0 逆用是指已知函數的單調性,求參數的取值范圍. 例3 已知函數f(x)=x2+2(a-1)x+2在區間(-∞,4]上是減函數,求實數a的取值范圍. 解f(x)=x2+2(a-1)x+2=[x+(a-1)]2-(a-1)2+2. 此二次函數的圖象對稱軸為x=1-a,開口向上. 可得1-a≥4,解得a≤-3. 實數a的取值范圍是(-∞,-3]. 點評本題考查的知識點是二次函數的圖象和性質,熟練掌握二次函數的圖象和性質是解答的關鍵. 點評本題主要考查用分離常數化簡函數的解析式,利用函數的單調性來解題. 由單調函數的定義易知,任何一個單調函數,在其單調區間上每個自變量與函數值之間是一一對應的.應用此性質解題是單調函數概念運用的一個重要方面. 例5 設f(x)=x3-3x2+6x-6,若f(a)=1,f(b)=-5,則a+b=( ). A.-2 B.0 C.1 D.2 解原函數可化為f(x)=(x-1)3+3(x-1)-2. 又f(a)=1,f(b)=-5,則可得(a-1)3+3(a-1)=3,(1-b)3+3(1-b)=3. 又設函數f(t)=t3+3t,故上面等式可化為f(a-1)=f(1-b).易知函數f(t)=t3+3t在R上是單調遞增函數,因此a-1=1-b,得a+b=2. 點評本題解題的關鍵是先將函數f(x)=x3-3x2+6x-6變形為f(x)=(x-1)3+3(x-1)-2(這也是求解此題的突破點)然后利用所得到的式子①構造函數f(t)=t3+3t最后利用函數f(t)的單調性奇偶性即可求解. 點評本題利用先變形函數關系式,進而對函數的單調性進行判斷,把原問題轉化為對函數單調性的討論,使問題迎刃而解. 即非單調函數問題(如不等式證明、求值等),通過構造,轉化為單調函數,再用單調函數的性質來解決. 例7 已知a、b、c∈R,|a|<1,|b|<1,|c|<1,求證abc+2>a+b+c. 解析考查目標不等式,可等價變形為(bc-1)a+2-b-c>0.視b、c為常量,a為變量,構造一次函數f(x)=(bc-1)x+2-b-c(|x|<1),由|b|<1,|c|<1,可知bc-1<0,所以f(x)在(-1,1)上是減函數.又-1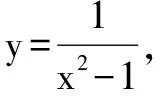
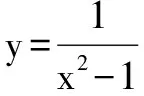
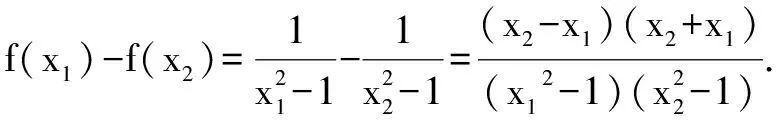

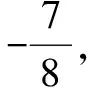
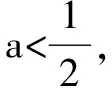
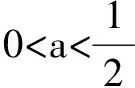
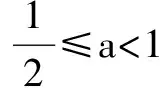

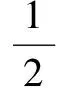
二、逆用
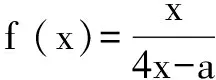
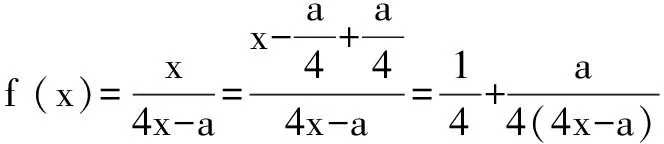
三、活用
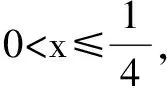
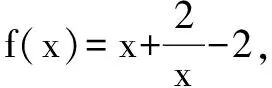
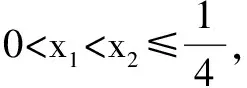
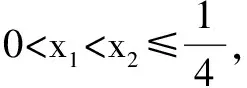
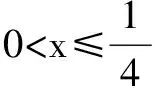
四、構造用

