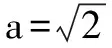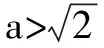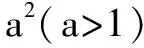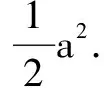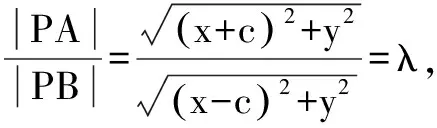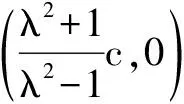由“橢圓與雙曲線的第一定義”想到的問題

韓景崗

(山東省鄒平縣黃山中學 256200)

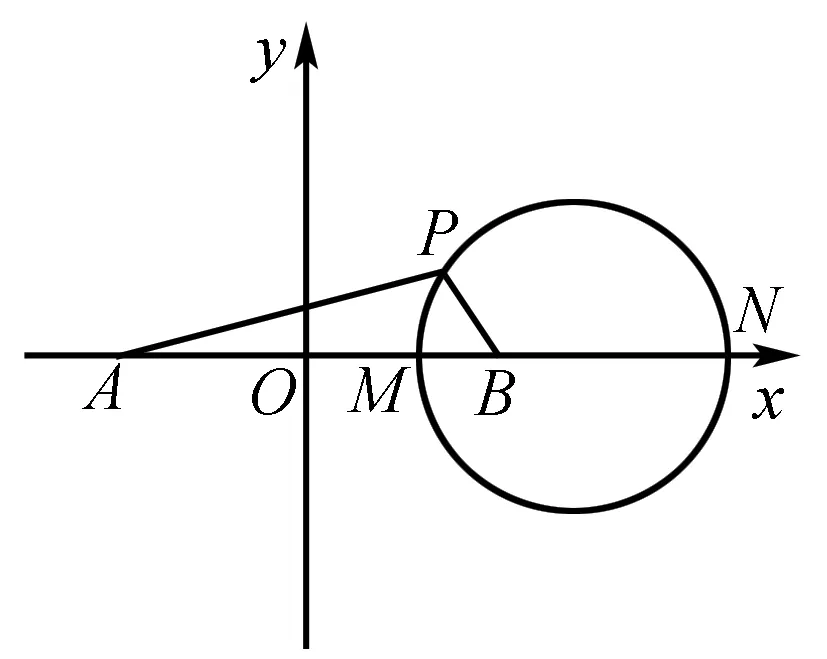
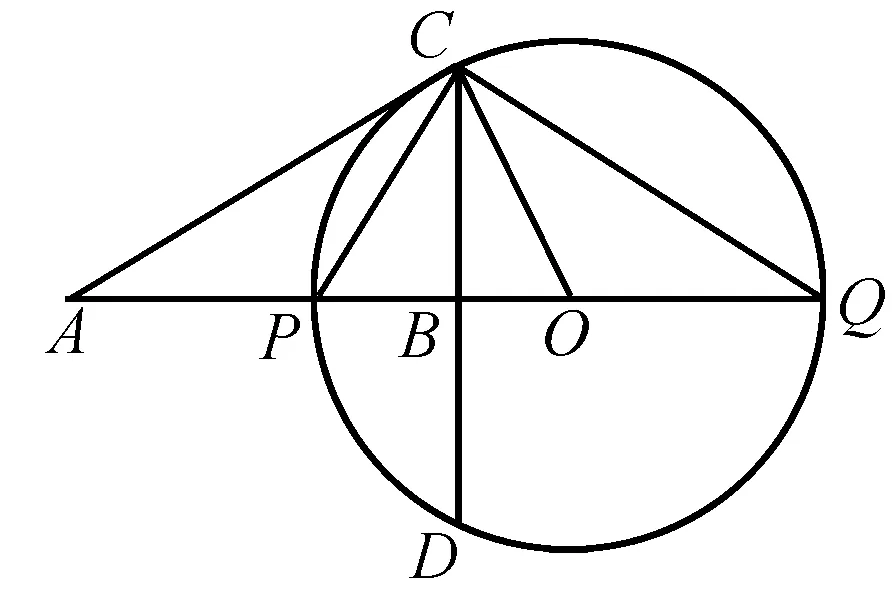
學習了橢圓與雙曲線的第一定義后，對于平面內一動點P與兩個定點A、B的距離和差為定值，則動點P的軌跡與橢圓、雙曲線有關，那我們可以進一步探究，由加減到乘除的運算時，動點P各自的軌跡方程如何？

例1 平面內兩定點A(-1,0)、B(1,0)，動點P滿足|PA|·|PB|=a(a≥0且a為常數)，那么動點P的軌跡是什么？

整理得(x2+y2)2-2(x2-y2)=a2-1，

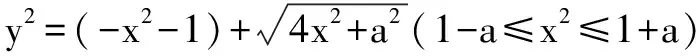
對于常數a≥0,可討論如下六種情況：

(1)當a=0時，曲線變為兩個點F1(-1,0),F2(1,0)；

(2)當0

(3)當a=1時，曲線成8字形自相交叉，稱為雙紐線；

評析這就是著名的卡西尼卵形線的特殊情況.

卡西尼卵形線，是平面內到兩個定點的距離之積為常數的點的軌跡，是環面曲線的一種.也就是說，平面內兩定點A(-a,0)、B(a,0)，動點P滿足|PA|·|PB|=b2(a≥0且a為常數)，那么動點P的軌跡方程是：

((x-a)2+y2)((x+a)2+y2)=b4或(x2+y2+a2)2-4a2x2=b4.

①曲線C過坐標原點；

②曲線C關于坐標原點對稱；

其中正確命題的序號為____.

評析上面動點P的軌跡被稱作阿波羅尼斯圓.

特別的當λ=1時，動點P的軌跡是線段AB的垂直平分線.

阿波羅尼斯圓有下面幾個常見的性質：

2.當λ>1時，點B在圓O內，點A在圓O外；當0<λ<1時，點A在圓O內，點B在圓O外.

3.直線AC為圓O的一條切線.若已知圓O及圓O外一點A，則可作出與點A對應的B，只要過點A作圓O的兩條切線，切點分別為C、D，連接CD與AO交于點B；反之，可作出與點B對應的點A.

4.過點A作圓O的切線AC(C為切點)后，CP、CQ分別為∠ACB的內、外角平分線.

在上面兩道例題的探究上，其實就是抓住教材中比較熟悉問題去聯想.可以發現，其實高考題也就是我們比較數學的內容引申升華一下而已，近年來的高考題越來越重視這種對思想方法的考查，隨著試題難度的上升，這樣的類比聯想等的方法會越來越重要.