賞析以數列為載體的八種創新題型

蔡勇全

(四川省資陽市外國語實驗學校 641300)

一、數學文化型

傳統數學文化源遠流長，是人類社會寶貴的知識與精神財富，需要人們大力弘揚與傳承，只有這樣，它本身所具有的價值才能得以釋放.數學文化型數列創新題正是在這種樸素理念的支撐下誕生的新題型，它以現時事件或歷史上一些數學名著中的某一段素材為背景，在基本不改變原意的前提下，巧妙地引出其中蘊含的數列問題，要求解題者求出該問題的結論，體現了數學的人文價值和科學價值.

例1 《九章算術》是我國古代第一部數學專著，全書收集了246個問題及解法，其中一個問題為“現有一根九節的竹子，自上而下各節的容積成等差數列，上面四節的容積之和為3升，下面三節的容積之和為4升，問中間兩節的容積各為多少?”該問題中第2節，第3節，第8節竹子的容積之和為( ).

解析自上而下依次設各節竹子的容積分別為a1，a2，…，a9，從而依題意可以得到

變式1 我國古代數學名著《算法統宗》中有如下問題:“三百七十八里關，初行健步并不難，次日腳痛減一半，六朝才得至其關，欲問每朝行里數，請公仔細算相還.”其意:有一個人走378里路，第一天健步行走，從第二天起，因腳痛每天走的路程為前一天的一半，走了6天后到達目的地，問此人每天走多少里路.則此人第五天走的路程為( ).

A.48里 B.24里 C.12里 D.6里

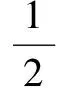
A.1260 B.1360 C.1430 D.1530

評注一般來說，數學文化型數列創新題的難度適中，命題者會將深澀的古文譯作通俗易懂的現代文，解題者不必心生畏懼，只需在準確理解現代譯文的基礎上，構建相應的數列模型，運用數列知識解出需要的數據，最后再回歸實際問題.

二、交匯整合型

一般數列的離散、有序性以及特定數列的遞推、趨向性等特點，決定了數列與其他數學知識之間有著千絲萬縷的聯系.交匯整合型數列創新題的基本特點是:形式多樣，內涵豐富，交匯點多，常常和函數、方程、不等式、三角、復數、概率與統計、解析幾何等知識融為一體，能夠很好地實現學科內、學科間知識的交匯整合.

變式已知曲線Cn:x2-2nx+y2=0(n=1，2，…).從點P(-1，0)向曲線Cn引斜率為kn(kn>0)的切線ln，切點為Pn(xn，yn).

(1)求數列{xn}與{yn}的通項公式；

評注教學中，既要讓學生掌握基礎知識和基本的數學思想方法，又要著力提高創新思維能力，認真研究、探索數列知識網絡的交匯性，研究交匯點向外輻射的知識塊，恰好能增強我們對學科知識的整體把握能力，又可以提高分析和解決創新型問題的能力.

三、規律發現型

規律發現型數列創新題的基本特點是:題目中已經給出某種數列的若干特殊數據或性質特征，可能要求歸納出該數列的一般規律、完善該數列的相應性質、類比推廣到相關數列等.

例3 以下依次是按照某種規律排列的一系列圖形中的第(1)～(4)個，由此可猜測第n個圖形中共有個圓圈.

思路二觀察上圖可以發現:第一個圖形只有一個中心圓圈；第二個圖形除中心圓圈外還有兩邊，每邊一個圓圈；第三個圖形除中心圓圈外還有三邊，每邊兩個圓圈；….按此規律，第n個圖形中除中心圓圈外還有n邊，每邊n-1個圓圈，故第n個圖形中圓圈的個數為n(n-1)+1=n2-n+1.

變式1 在德國不萊梅舉行的第48屆世乒賽期間，某商場櫥窗里用同樣的乒乓球堆成若干堆“正三棱錐”形的展品，其中第1堆只有一層，就一個球，第2，3，4，…堆最底層(第一層)分別按如圖所示的方式固定擺放，從第二層開始，每層的小球自然壘放在下一層之上，第n堆第n層就放一個乒乓球，則第n堆的乒乓球總數f(n)=.

變式2 在正整數數列中，由1開始依次按如下規則，將某些數染成紅色.先染1；再染兩個偶數2，4；再染4后面最鄰近的3個連續奇數5，7，9；再染9后面的最鄰近的4個連續偶數10，12，14，16；再染此后最鄰近的5個連續奇數17，19，21，23，25.按此規則一直染下去，得到一紅色子數列1，2，4，5，7，9，10，12，14，16，17，…，則在這個紅色子數列中，由1開始的第2018個數是( ).

A.3971 B.3972 C.3973 D.3974

評注從例3及其變式的解答過程可以看到，解決規律發現型數列創新題需要解題者具有較強的觀察能力和快速探求規律的能力，因此平時應注重這方面的訓練和經驗的積累.

四、現時約定型

現時約定型數列創新題的基本特點是:以已有數列知識為基礎，現時定義一個新的概念，然后圍繞新概念設計一系列問題.此類問題旨在考查學生獨立獲取信息、加工信息的閱讀理解能力和知識的運用、遷移能力.

例4 已知數列{an}滿足an=logn+1(n+2)(n∈N*)，定義使得a1·a2·a3·…·ak為整數的正整數k叫做“契合值”，則區間(6，2018]內的契合值的個數為，該區間內所有契合值的和為.

變式把形如M=mn(m，n∈N*)的正整數M表示成各項都是整數，公差為2的等差數列的前m項的和，稱為“對M的m項分劃”.例如，把9表示成9=32=1+3+5，稱為“對9的3項分劃”；把64表示成64=43=13+15+17+19，稱為“對64的4項分劃”.據此，對324的18項分劃中最大的數是；若M=m3的m項分劃中第5項是281，則m的值是.

評注例4及其變式代表了現時約定型數列創新題的兩種最常見形式，即定義新名詞性術語與定義新規則性術語，解決此類問題時應充分理解新定義，并緊扣新定義與所學的知識，從而找到解題突破口.

五、數表(陣、組)型

數表(陣、組)型數列創新題的基本特點是:將一些數排成長方形、三角形、數組的形式，就形成了數表、數陣等形式，要求學生研究某行、某列、某組或所有行(列、組)所具有的特殊性質.

例5 在n行m列的方格表中每一個方格都填上一個數，使得每一行的m個數與每一列的n個數都成等差數列，如果表的四個角上的數之和等于S，則此表中所有數的和等于.

a11a12…a1m…………an1an2…anm

變式1 在如圖所示的三角形數陣中，第n行共有n個數，且該行的第一個數和最后一個數都是n，中間任意一個數都等于第n-1行與之相鄰的兩個數之和，an1，an2，…，ann(n=1，2，3，…)分別表示第n行的第一個數，第二個數，…，第n個數，求an2(n∈N*且n≥2)的通項式.

(1)第1組到第k組共有幾個數?

(2)第k組中的首數和尾數各是多少?

(3)求第k組中各數之和及前k組中各數之和.

評注從例5及其變式的解答過程可以看到，求解此類問題的策略是通過觀察、分析，弄清楚數表(陣)中各行(列)的項與列(行)數之間的對應關系或所有數組中的數的總體趨勢，然后再轉化成熟悉的等差或等比數列問題求解.

六、逆向探索型

逆向探索型數列創新題的基本特點是:可能題設中已經給出了具有某種特征的數列，要求尋找這一特征產生的條件，也可能是將數列是否具有某種特征作為一個待定的問題，要求分析數列具有該特征的條件和不具有該特征的原因.

綜上所述，a1=56或9.

變式已知數列{an}的前n項和Sn=3n2+5n，數列{bn}中，b1=8，64bn+1-bn=0.問:是否存在常數c，使得對任意的正整數n，an+logcbn恒為常數m?若存在，求出常數c和m的值；若不存在，請說明理由.

評注從例6及其變式的解答過程可以看到，此類問題主要考查學生逆向思維能力，解題策略是從數列已經具有的某一特征出發進行逆向性的邏輯推理，或假設數列具有某種特征，再進行逆向性的演繹推理，若出現矛盾，則可否定假設，若推證無矛盾，則假設成立.

七、性質探求型

認識性質探求型數列創新題的基本特點，需要明確:數列是一類特殊的函數，一方面，它的定義域只能為正整數集或其子集；另一方面，函數的性質常常可以創新設置在數列問題中，比如從函數角度分析判斷數列的周期性、有界性、單調性、求具體項、求最大(小)項等問題.

A.f(n+1)-f(n)=1

B.f(n+k)=f(n)(k∈N*)

C.αf(n)=f(n+1)+αf(n)(α≠0)

D.αf(n+1)=α-(α+1)f(n)(α≠0)

評注從例7及其變式的解答過程可以看到，解決此類問題的策略是通過對數列形式的挖掘得出數列特有的性質，從而達到化歸轉化解決問題的目的，其中性質探求是關鍵.值得一提的是，例7不僅是性質探求型數列創新題，而且解答時用到了三角代換技巧，因此它也屬于解法創新型數列題，當然，這需要解題者具有靈活而廣博的解題思維.

八、類比聯想型

類比聯想型數列創新題的基本特點是:題目中給出某種特殊數列的屬性，要求解答者根據所給信息與另一種特殊數列的相似性或一致性，為之寫出類似的結論，這里的屬性可以是問題的結論、分析思路，解題方法、式子的結構等.

例8 已知數列a1，a2，…，a30，其中a1，a2，…，a10是首項為1，公差為1的等差數列；a10，a11，…，a20是公差為d的等差數列；a20，a21，…，a30是公差為d2的等差數列(d≠0).

(1)若a20=40，求d；

(2)試寫出a30關于d的關系式，并求出a30的取值范圍；

(3)續寫已知數列，使得a30，a31，…，a40是公差為d3的等差數列，…，以此類推，把已知數列推廣為無窮數列，類比(Ⅱ)問，你能提出什么樣的問題，還能得到什么樣的結論？

提示(1)a10=1+9=10，a20=10+10d=40，所以d=3.

(3)所給數列可推廣為無窮數列{an}，其中a1，a2，…，a10是首項為1，公差為1的等差數列，當n≥1時，數列a10n，a10n+1，…，a10(n+1)是公差為dn的等差數列，類比(Ⅱ)問，研究的問題可以是:試寫出a10(n+1)關于d的關系式，并求a10(n+1)的取值范圍.

變式在等差數列{an}中，若a10=0，則a1+a2+…+an=a1+a2+…+a19-n(n∈N*且n<19)成立.類比上述性質，相應地，在等比數列{bn}中，若b9=1，則有等式成立.

提示首先研究a1+a2+…+an=a1+a2+…a19-n成立的理由.因an+1+a19-n=2a10=0,an+2+a18-n=2a10=0,an+3+a17-n=2a10=0,…,故an+1+an+2+an+3+…+a17-n+a18-n++a19n-n=0，兩邊同時加上a1+a2+…+an，故有上式成立.

評注由例8及其變式的解答過程可以看到，解決此類問題的策略概括起來就是引申、推廣、遷移、移植等幾個關鍵詞，但需要注意的是，由此得到的一般性結論可能真，也可能假，結論的正確性有待進一步證明.