基于多項式回歸的Pair-Copula貝葉斯網絡模型

牛巖溪，梁馮珍

（天津大學 數學學院，天津 300350）

0 引言

貝葉斯網絡(Bayesian networks)也稱信念網絡(Belief networks)，是描述隨機變量間依賴關系的圖形模式，被廣泛用于不確定性問題的智能化求解。該網絡由有向無環圖(DAG)和概率參數構成。DAG的節點表示隨機變量，節點間的有向弧表示變量間的相依關系，具體的相依程度則通過概率參數反映。1988年，Pearl[1]首先給出其嚴格定義，并創建貝葉斯網絡基礎理論體系。貝葉斯網絡具有多功能性、有效性和開放性等特征，能夠有效地轉化數據為知識，并利用這些知識進行推理，以解決分析、預測和控制等方面的問題。Kurowicka和Cooke(2002)[2]將Pair-Copula和貝葉斯網絡結合，在繼承了一般貝葉斯網絡結構的優點的同時，結合Copula函數的優良性質，建立一種新的多元統計模型——Pair-Copula貝葉斯網絡(PCBNs)模型。PCBNs模型通過結構推斷和相關性分析，反映變量之間的因果相依關系，為各領域研究人員和管理者提供決策支持，近年來已在金融、工程等領域有所應用。

構建Pair-Copula貝葉斯網絡模型包括結構估計和參數估計。Bauer等(2012)[3]給出了DAG模型下Pair-Copula的ML參數估計的方法。結構估計常用的機器學習方法有PC算法[4]、爬山(Hill-climbing)算法等。Colombo(2012)[5]對經典PC算法模型進行了改進，降低了檢驗順序對檢驗結果的影響。然而，在結構估計中，核心步驟是變量之間條件獨立性的檢驗。條件獨立性檢驗的難度要遠遠大于非條件獨立性檢驗。Bouezmarni等（2009）[6]基于Hellinger距離，結合Bernstein Copula構造了檢驗統計量來檢驗條件獨立性。Zhang（2011）[7]提出基于核函數的條件獨立檢驗方法。Ramsey等（2014）[8]對核函數模型進行了簡化和推廣。

本文在改進的PC算法的基礎上，提出基于多項式回歸殘差的條件獨立性檢驗方法，并進行仿真模擬實驗以及氣象數據實證分析。該方法可以良好地檢驗變量間的條件獨立關系，使用網絡結構體現變量間的相依和獨立關系，并結合Pair-Copula得到完整的相依關系推斷模型以及相應的聯合密度函數。

1 Pair-Copula貝葉斯網絡模型

當變量集給定時，構建Pair-Copula貝葉斯網絡主要包括結構估計和參數估計。Pair-Copula貝葉斯網絡允許在變量的子集間定義條件獨立性，這也是貝葉斯網絡最重要的性質之一。在結構估計中，該性質將變量間的條件獨立關系從復雜的網絡中除去，大大簡化了網絡模型結構和相應的聯合密度函數的復雜程度，使得變量間的相依和獨立關系可以通過簡潔的有向無環圖直觀地展現。檢驗變量間的條件獨立性在Pair-Copula貝葉斯網絡的構建和相依關系的發現中尤為重要。

1.1 馬爾科夫概率測度

在圖形模式中，和變量條件獨立性相對應的是節點的D-馬爾科夫屬性。令V≠?為一個有限集合，E?E={(v,w)∈V×V|v≠w}。則D=(V,E)表示一個由頂點集V和邊集E構成的DAG，Dm為D的道德圖[3]。對于任意v∈V，令：

令P為?d上的概率測度，d=|V|。X為?d上概率分布為P的d維隨機變量。對于I?V，記XI=(Xv)v∈I。若對于兩兩互不相交的集合I,J,K?V，有XI和XJ在給定XK的條件下獨立，則記為XI⊥XJ|XK。

當對于?v∈V，有：

則稱P具有局部D-馬爾科夫屬性。

當對于兩兩互不相交的集合I,J,K?V，有：

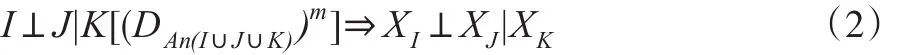
則稱P具有全局D-馬爾科夫屬性，其中An(?)表示最小祖先集。當概率測度滿足式（1）和式（2）時，則稱P具有D-馬爾科夫屬性。D-馬爾科夫屬性可以更進一步地展示出由有向無環圖D表示的條件獨立性。

現令P有Lebesgue概率密度f，則P是D-馬爾科夫的當且僅當f有如下形式的D-遞歸因式分解：

其中fv|pa(v)(?|xpa(v))表示在給定Xpa(v)=xpa(v)的條件下，Xv的條件概率密度函數[3]。

1.2 Pair-Copula貝葉斯網絡模型

令D=(V,E)為一個DAG，P為?d上絕對連續的D-馬爾科夫概率測度，d=|V|。X為?d上概率分布為P的d維隨機變量。對于?v∈V，s.t.|pa(v)|≥1 ，令wv:{1,…,|，是一個雙射。令＜v為pa(v)上的一個全序關系，在這個關系中，?i,j∈{1,…,有i＜j當且僅當wi＜vwj。則?v∈V，w∈pa(v)，記：

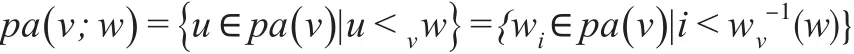
由Sklar定理[9]可知，P的概率密度函數可以唯一地分解成一元邊緣密度函數fi和Copula函數c的形式。Bauer等(2012)[3]指出c又可以進一步分解成（條件）成對Copulacv,w|pa(v;w)的形式，其中每個條件Copula關系對應于DAG中的一條邊w→v，cv,w|pa(v;w)表示相應密度函數。因此，P的概率密度函數f可以寫成如下形式：

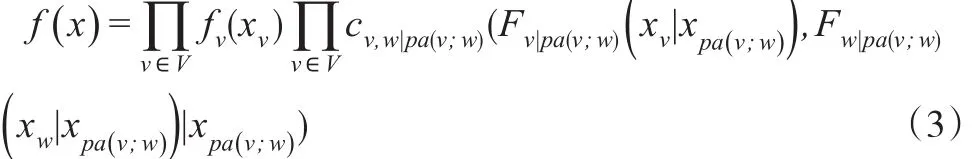
其中x=(xv)v∈V∈?d。

令u=(u1,…,un)，n?? ，是 [0,1]d上的隨機變量U的i.i.d.觀測值，其Copula分布族為{CD;θ|θ∈Θ}，邊緣分布為均勻分布。則式（3）對應的對數似然函數為：

同樣作為由Pair-Copula構成的圖結構，Vine-Copula結構也是數據建模中常用模型之一。Vine-Copula方法隨著變量維度的增加，可選結構的種類以及待估參數數量將隨之以平方函數速度增加，運算量較大。從式（3）的聯合密度函數表達式可以看出，Pair-Copula貝葉斯網絡結構與Vine-Copula結構相似，但卻剔除了條件獨立變量之間的關系。易知，建立一個d維Regular vine(R-vine)模型結構[9]，需要定義的Pair-Copula數量為而由于考慮了條件獨立性，Pair-Copula貝葉斯網絡結構所需Pair-Copula數量將減少。隨著維度增加，這個優勢會更加凸顯。

1.3 基于多項式回歸的條件獨立性檢驗

給定變量集，構建Pair-Copula貝葉斯網絡的首要任務即利用變量間的馬爾科夫屬性識別DAGD=(V,E)。因此，檢驗變量間的條件獨立性在貝葉斯網絡的構建和相依關系的發現中尤為重要。改進的PC算法[5]是一種數據驅動下的網絡結構估計算法。在此算法的基礎上，本文提出一種基于多項式回歸判斷變量間條件獨立性的方法。

根據數學分析中的知識易知，任何函數都可以近似地用多項式表示。因此，兩個變量間的關系可以用多項式進行逼近，即多項式回歸，變量無關部分則通過回歸殘差反映。相較于核回歸，多項式回歸在處理實際問題中更為常用，使用方便且容易解釋。多項式回歸模型的一般形式為：

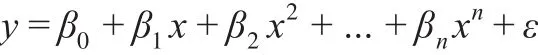
下面給出在多項式回歸模型下的條件獨立性判斷方法。

設X,Y,Z為?上的隨機變量，X和Y在給定Z的條件下獨立，當且僅當但高維時，估計密度函數困難。因此，本文避開明確的密度估計，考慮X,Y,Z間的非線性回歸，而不做其他的分布或函數結構的假設。

本文選用多項式回歸模型，認為X和Y在給定Z的條件下獨立，當且僅當Z回歸到X的殘差與Z回歸到Y的殘差之間相互獨立。即：

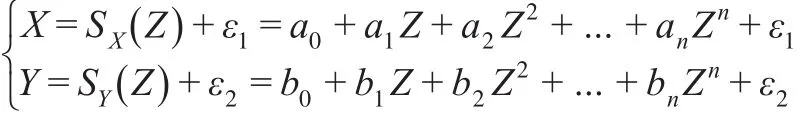
其中SX和SY為多項式函數，則：

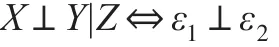
不同于非條件獨立關系，當給定Z時，X和Y的關系無法直接獲得。通過多項式回歸，分別從X和Y中將Z的影響分離，與Z不相關的部分放在誤差變量ε中。此時，本文將復雜條件獨立性的判斷轉化為了非條件獨立性的判斷。不同于數理統計中關于兩變量獨立的嚴格定義，在實際應用中，絕對獨立的情況并不常見，因此在本文所建模型之下，認為給定Z時，X和Y不相關即可判定為條件獨立。此處可以選取任意一種合理的相關系數來檢驗ε1,ε2之間是否相關。

1.4 基于多項式回歸的PCBNs模型構建

獲取實際數據，對數據做一定的預處理，構建Pair-Copula貝葉斯網絡，主要步驟如下：

步驟1：結構估計。

對樣本使用改進PC算法進行歷遍，其中獨立性檢驗步驟改為上述多項式回歸方法。由所有節點的完全無向圖[3]出發，假設節點順序未知。

若εiK⊥εjK，接受原假設H0，刪去邊i-j；否則拒絕原假設H0，保留邊i-j。此時，條件獨立性的判斷被轉化為相對簡單的非條件獨立性的判斷，本文選取Kendall相關系數(Kendall’sτ)，若|τ|較小，εiK與εjK不相關，則判斷

此時DAG對應的無向圖[3]得到，記為DU。

步驟2：方向確定。

無向圖DU確定后，需確定邊的方向。設Sij為i,j的分割集，i≠j∈V，(i,j)?EDU，(i,j)?EDU。

對于i∈V，j?ad(i)，k∈ad(i)∩ad(j)，如果k?Sij，則i-k-j的方向為i→k←j。（v-結構）

當尋找到所有存在的v-結構后，其他無向邊方向規則為：

若DU中包含i→j且k?ad(i)，則j-k方向為j→k（否則將存在新的v-結構）。

若DU中包含i→k→j，則i-j的方向為i→j（否則將存在環結構）。

若DU中包含i→k→j和i→I→j，l?ad(k)，則i-j的方向為i→j（否則將存在新的v-結構或環結構）。

只使用馬爾科夫性質，有時不足以得到完整的相依關系，可能存在某些邊的方向無法確定的情況，但可作為進一步探索的起點。實際應用中，可以根據數據的具體情況，結合其他方法和經驗確定或修改方向。所有邊方向確定后，得到有向無環圖D對應的鏈圖[3]D*。

步驟3：參數估計。

確定邊對應的條件相依關系。結合Vine-Copula結構的參數估計方法，為各邊構造藤結構，進行參數估計[3]。本文選取D-vine結構，首先求樣本的經驗分布函數，用于Copula建模。由于網絡結構的方向確定，因此可以確定每個節點的祖先集，對于D中i∈V，j∈ad(i)，k?an(i)∩an(j)，根據D-vine的參數估計方法，為邊構造一個或多個藤結構，估計所有(xi,xj)|xk的Pair-Copula類型及參數，求得參數對應的Kendall’sτ值，結合實際問題選取|τ|較大的作為該邊的相關關系。由于本文主要使用獨立性關系作為抽樣依據，對于相依關系的依賴較少，因此條件集的選擇范圍也較寬，在實際問題應用中十分靈活。Pair-Copula函數類型和參數確定后，即可寫出相應的聯合密度函數，并得到最終的Pair-Copula貝葉斯網絡。

2 仿真模擬

本文考慮一個簡單的5節點貝葉斯網絡，樣本容量為5000，使用R語言編寫程序。假設給定網絡模型以及變量間的相依關系如圖1所示。在該網絡中，變量間的條件獨立關系為2⊥3|1，1⊥4|(2,3)，1⊥5|4，2⊥5|4，3⊥5|4 。首先確定抽樣方法，對樣本使用上次中的步驟，構建完整Pair-Copula貝葉斯網絡。

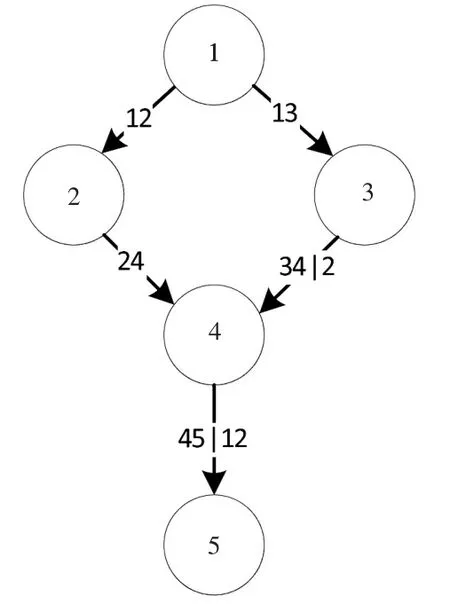
圖1 5節點貝葉斯網絡

2.1 抽樣方法

根據條件獨立關系和相關關系構造變量之間的多項式組，用于抽樣。由于任何函數都可用（分段）多項式形式表示，因此可以任意構造能體現相應的獨立、相關關系多項式。在多項式回歸中，當自變量的冪超過3時，回歸系數的解釋將變得困難，回歸函數也變得很不穩定，對回歸模型的應用會受到影響。因而，冪次超過3的模型不常使用。本文以二次方多項式為例，建立如下多項式關系：

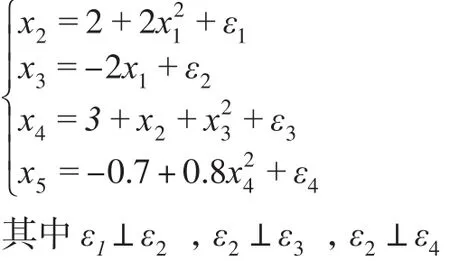
抽樣步驟如下：

步驟1：根據殘差的獨立關系，利用獨立高斯Copula生成殘差ε1,ε2,ε3,ε4。

設ε1,ε2,ε3,ε4為 回 歸 殘 差 ，ε1⊥ε2，則 (ε1,ε2)～GassianCopula(0,dim=2)，生成兩組聯合分布為獨立高斯Copula的隨機數，分別賦予ε1,ε2。生成（0,1）上均勻分布隨機數w3～U(0,1)，w4～U(0,1)，根據ε2⊥ε3，有為獨立高斯 Copula的條件逆Copula函數。同理

步驟2：根據多項式關系生成樣本。首先需生成（0,1）上均勻分布隨機數u1。

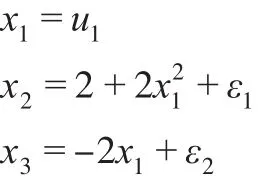
此時模擬樣本得到。

2.2 結構估計

根據1.4中的步驟1，由所有節點的完全無向圖出發檢驗條件獨立性，如圖2所示。使用基于多項式回歸的改進PC算法進行節點歷遍后，得到邊的具體刪留情況如表1所示，此時DAG對應的無向圖確定，記為DU。

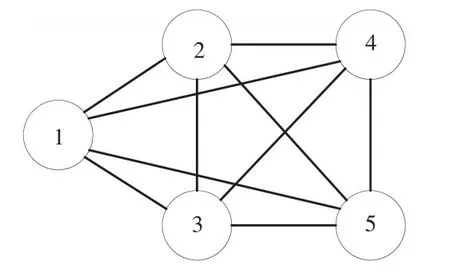
圖2完全無向圖

表1 完全無向圖邊的刪留情況

在該例中，5節點結構到此歷遍結束。對于更高維的數據，可以不考慮條件集長度大于3的情況，或僅作為參考，綜合前幾層歷遍決定邊的刪留。

根據1.4中的步驟2，當通過v-結構及其他無向邊方向規則為無向圖確定方向后，得到鏈圖D*，如圖3所示，此時仍有兩條邊不能完全確定方向，即1—2和1—3。實際問題中可根據情況或結合其他方法確定。暫且假定為1→2，1→3。此時網絡完整結構得到，如圖4所示。

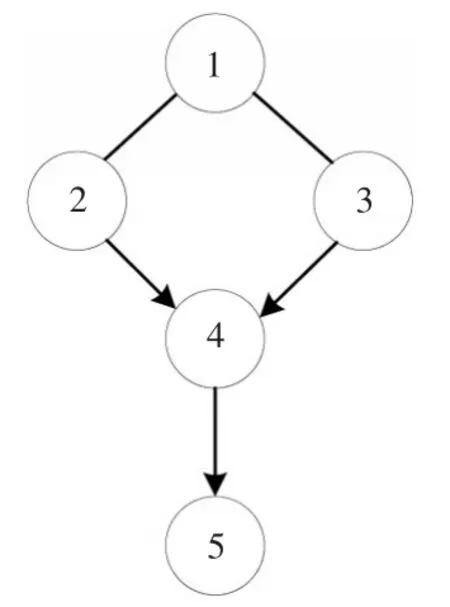
圖3 鏈圖D*

圖4有向無環圖D

2.3 參數估計

網絡結構確定后，并不能最終確定每條邊對應的條件相依關系。如邊4→5，對應的關系可能是45|12、45|123或其他。根據1.4中的步驟3，為邊構造藤結構確定Copula類型，估計參數。本文只考慮Copula函數中最常見的幾種函數類型。

最終得到的Pair-Copula類型及參數如表2所示：

表2 Copula類型及參數

聯合密度函數為：

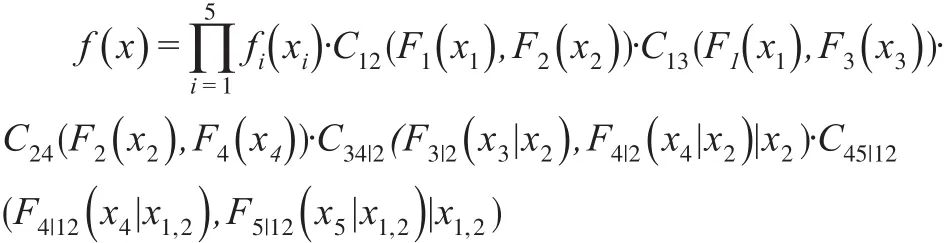
Pair-Copula貝葉斯網絡得到，如圖5所示：

圖5 Pair-Copula貝葉斯網絡

3 實證

在空調系統設計過程，室外氣象參數是負荷計算、設備選型等必需的基礎參數，直接影響系統設計和運行效果。氣象參數之間具有一定程度的相依關系，本文選取四種典型參數：干球溫度、濕球溫度、含濕量、太陽輻射，將上文介紹的方法應用到逐時氣象數據中進行實證分析，探討這四種氣象參數之間的相關性。數據來自天津市氣候中心，選取天津市2010年全年逐時干球溫度、濕球溫度、含濕量、太陽輻射觀測值，每項觀測值包含8760個數值。

設干球溫度、濕球溫度、含濕量、太陽輻射依次為變量x1,x2,x3,x4。根據物理意義及現實情況，溫度、濕度等空氣狀態受太陽輻射強度影響，反之，太陽輻射不受溫度等影響，因此確定太陽輻射為首層節點，不考慮在其他變量的條件下太陽輻射與某一變量的關系，即只考慮太陽輻射與其他變量的無條件關系。其他變量的節點順序未知。

首先使用基于多項式回歸的改進PC算法進行節點歷遍，選取|τ|=0.3 ，若|τ|＜0.3 認為變量間（條件）不相關，判定滿足條件獨立性。得到邊的具體刪留情況如表3所示。

表3 氣象數據完全無向圖邊的刪留情況

按照方向規則為無向邊確定方向，得到DAG如下頁圖6所示。

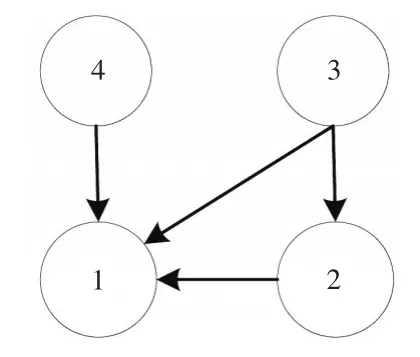
圖6氣象數據有向無環圖

網絡結構確定后，將數據變換為Copula水平。由于本文重在研究相關結構，不對邊緣分布做具體研究，因此通過經驗概率積分變換將逐時干球溫度、濕球溫度、含濕量、太陽輻射變換為Copula數據。考慮每條邊可能對應的所有（條件）關系，估計Pair-Copula類型及參數，并求得參數對應的Kendall’sτ值，結合實際情況和τ值，選取該邊的相關關系。最終得到的Pair-Copula類型及參數如表4所示：

表4 氣象數據Copula類型及參數

Pair-Copula貝葉斯網絡如圖7所示。

圖7氣象數據Pair-Copula貝葉斯網絡

從上述Pair-Copula貝葉斯網絡看出，干球溫度與含濕量、太陽輻射有關；太陽輻射給定時，濕球溫度與含濕量相關；含濕量給定時，干濕球溫度相關。從物理意義角度分析，干球溫度是溫度計自由地被暴露在空氣中所測量的溫度，通常被視作所測量空氣的實際溫度，與含濕量、太陽輻射有關。濕球溫度是溫度計的球體表面附著有水時，水份蒸發帶走熱量后球體的溫度。太陽輻射給定時，水的蒸發量跟空氣的濕度有關，空氣濕度越大蒸發量越小，帶走的熱量越少，干濕球溫度差異越小；空氣濕度越小水蒸發量越大，帶走的熱量也越大，干濕球溫差也就越大。通過該Pair-Copula貝葉斯網絡可以推斷當某一變量發生變化時，干球溫度的變化情況。

4 總結

Pair-Copula貝葉斯網絡能夠有效地轉化數據為知識，并利用這些知識進行推理，以解決因果推斷等問題。在改進的PC算法的基礎上，多項式回歸殘差的條件獨立性檢驗方法可以良好地檢驗變量間的條件獨立關系，結合Pair-Copula得到完整的相依關系推斷模型及聯合密度函數。在節點個數較少的情況下，該方法簡單有效，適用于在實際應用中解決金融、工程等領域的相關問題。當節點個數較多時，可綜合其他方法進一步研究探討。