基于混合神經網絡模型預測下的統計套利研究

鄧曉衛，章鋮斌

（南京工業大學a.數理科學學院；b.海外教育學院，南京 211800）

0 引言

統計套利通過對歷史數據進行統計分析，從一組資產的定價偏差中獲利。價差的波動率決定了套利的成本和收益，而套利資產組合價格收斂是套利策略的基本保證。目前為止，國內外關于統計套利的研究，主要針對于各種期貨產品的套利策略研究[1-4]。隨著機器學習研究的深入，學者們發現建立在機器學習方法上的預測比一般時間序列的預測模型要更精準[5-8]。于是有學者將神經網絡模型運用在統計套利中，如：徐顥華等[9]引入差分BP神經網絡及拓撲結構對股指期貨進行預測，檢驗其預測結果好于普通BP神經網絡預測，提出可用于套利；靳朝翔等[10]以焦炭、鐵礦石和螺紋鋼為例，基于NAR動態神經網絡模型研究套利策略；劉陽等[11]將神經網絡模型與動態GARCH模型相結合，提出了一種基于信息更新NN-GARCH模型，對大連商品交易所的大豆一號和二號的統計套利策略進行了研究。

綜上，關于統計套利的研究特點是：第一，在研究對象上，大部分以期貨產品為主，且套利產品一般是基于兩個產品進行；第二，在研究方法上，基本還是采用協整分析、誤差修正模型等方法。雖然基于神經網絡的統計套利有初步的研究，但研究的方法和對象還十分欠缺。如文獻[9]提出的差分BP神經網絡模型可用于套利但并未對此真正展開研究。而且，這些研究都是基于較為基礎的神經網絡模型。本文的創新點在于：第一，就交易對象而言，選擇國內股票市場進行研究，并且考慮多元投資組合的統計套利策略；第二，基于LSTM和BP神經網絡模型，提出一個混合神經網絡模型，并應用Google公司開發的最新機器學習框架Tensorflow進行統計套利研究。

1 混合神經網絡模型

BP神經網絡是一種多層的前饋神經網絡，從激勵函數Sigmoid函數開始：

然后通過隱含層的輸出、輸出層的輸出、誤差的計算、權值的更新、偏置的更新等步驟進行迭代，最終得到較理想的結果。

LSTM（Long Short-Term Memory）是一種時間遞歸神經網絡，由通過精心設計的稱作“門”的結構來去除或增加信息到細胞狀態的能力，他們包含一個Sigmoid神經網絡層和一個Pointwise乘法操作。LSTM擁有三個門（遺忘門、輸入門、輸出門）來保護和控制細胞狀態。LSTM神經網絡模型經過眾多學者和研究人員改進，目前已被廣泛用于多個領域，如語言翻譯、圖像識別、預測疾病、點擊率、股票等。

由于LSTM神經網絡在處理和預測時間序列中間隔和延遲相對較長的數據、學習長期依賴信息方面具有優勢，故本文擬將LSTM模型用于統計套利的前期預測。但在對該模型實際運用時發現，單純運用LSTM神經網絡模型做預測，預測區間的前段效果并不是十分理想。于是本文提出一種混合神經網絡模型，即在LSTM神經網絡模型基礎上引入BP神經網絡模型進行預測修正，使得預測值更精準，最終提高了統計套利結果。具體步驟如下：

首先，將所有數據集分為訓練集、測試集和預測集，用LSTM神經網絡模型進行訓練、測試和預測，預測值記為yLSTM；然后，將原先的訓練集和測試集的數據重新分為新的訓練集、測試集和預測集，記為訓練集1、測試集1和預測集1，重復LSTM神經網絡預測步驟，得到預測集1與真實數據誤差的時間序列；最后，對該時間序列進行BP神經網絡學習，得到預測集的誤差項的變化，記為εBP，以此對yLSTM不太穩定的前段進行修正，得最終預測值為：

式（2）即為一個混合神經網絡模型。下文將通過實證檢驗該混合模型的預測精度高于單純用BP預測的精度。

2 混合神經網絡模型套利策略

首先，由長期協整關系選出可能進行套利的n個資產，設為x1t，x2t，…，xnt（此處亦表示各資產的收盤價）；采用文獻[9]的方法，可得該資產組合t時刻的利潤為：

其中，ut=x1t-α1x2t-α2x3t-…-αn-1xnt右端各系數通過最小二乘擬合來確定。在確定各資產權重αi后，采用本文提出的混合神經網絡模型，按累積疊加的方式用xit的前t個值去預測第t+1個值，再得到預測的利潤函數序列{proft}。

然后，對時間序列{proft}進一步分析，通過建立ARMA(p,q)模型，從中分離出隨機擾動項εt（此為白噪聲序列），本文的統計套利是通過對擾動項εt的預測值來設計套利策略。經過多次嘗試，最后選擇的是ARMA(1,1)模型如式（4）所示：

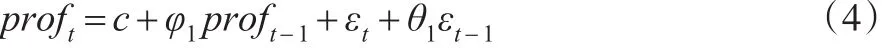
最后，統計套利最重要的是分析套利中出現的時機和概率。為此，本文先確立套利區間，使用上述模型計算得到殘差εt，并且假設交易閾值為λ1和λ2，則λ1εt和 -λ1εt為交易（買空、賣空）的上下界。同時設立平倉的最大區域，設置λ2εt和 -λ2εt為平倉上下限。這里，λ1，λ2＞0 ，且λ2＞λ1。

建立套利的頭寸后，當價差序列如期回歸到μ±λi εt(i=1)區間時（μ為均值，此處為0）進行反向操作獲利，從而完成一次正向或反向的套利。如果沒有如期回歸至標準差區間，本文設定了平倉上下限，即當價差觸發μ±λiεt(i=2)以外的區域時，多頭頭寸或空頭頭寸立即平倉止損。該策略是基于風險管控的交易策略，為了避免過大的波動風險。

3 實證分析

3.1 數據選取及預處理

根據統計套利的相關理論，先找具有較高相關性的股票來作為研究樣本。通過計算相關系數，本文選取了相關性較高的4只股票：中國銀行、工商銀行、農業銀行和建設銀行四大國有銀行2016年1月1日至2017年9月30日每日開盤價、收盤價、最高價、最低價、復權價1、成交量、成交金額、振幅作為研究樣本，用這8個變量使用混合神經網絡模型對下一交易日的收盤價進行預測。數據來源于銳思金融數據庫。混合神經網絡模擬所用的程序基于TensorFlow框架，這是谷歌研發的第二代人工智能學習系統，并在2015年11月9日宣布開源，利用Python語言對此進行控制。統計軟件使用Eviews10.0。

3.2 平穩性及協整檢驗

進行套利的組合產品需要滿足協整關系。首先，對樣本數據進行平穩性檢驗以確定他們的單整階數。此處采用ADF檢驗。記x1t、x2t、x3t、x4t為工商銀行、建設銀行、農業銀行、中國銀行第t天的股票收盤價價格。對4只股票的收盤價及收盤價差分序列作ADF檢驗，結果顯示①限于篇幅，此處省略了ADF的全部檢驗結果。：四家銀行股票收盤價格序列均不平穩，但其一階差分序列在1%的水平下均是平穩序列，即他們具有相同的單整階數：{xit}～I(1)，i=1，2，3，4 。

其次，用E-G兩步法對x1t、x2t、x3t、x4t進行協整關系檢驗。同時為了分析不同投資組合及不同神經網絡模型在統計套利中的獲利差異及優劣，本文以所選的4只股票為基礎構造了四種投資組合（見表1），分別對他們進行協整檢驗。

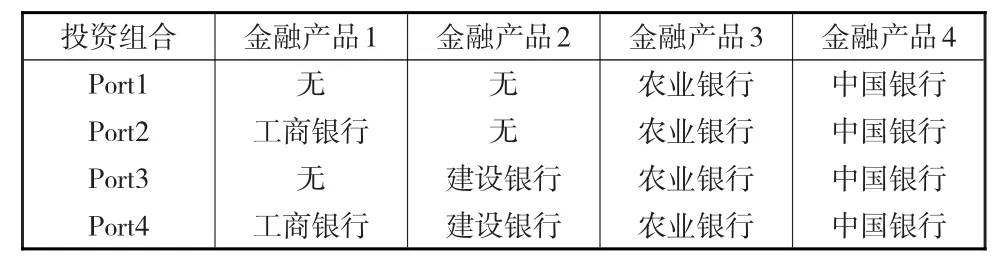
表1 投資組合列表

先對Porti，(i=1，2，3，4)進行OLS回歸，以獲取殘差項uit，i=1，2，3，4 。再對該殘差序列分別進行單位根檢驗，結果如表2所示。

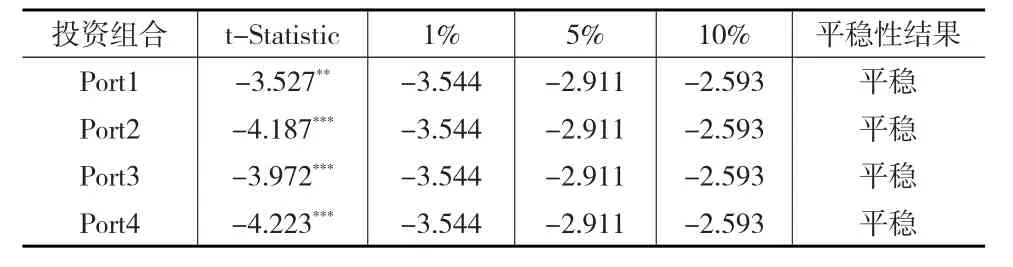
表2 uit的單位根檢驗結果

結果顯示，四組殘差序列在1%或5%的置信水平下均平穩，從而所構造的四個組合均存在長期的協整關系。

3.3 套利策略制定

根據式（3）定義，該四種組合的套利收益可以表示為：其中，uit，t=1，2，3，4 。由前OLS回歸結果確定，具體如下：

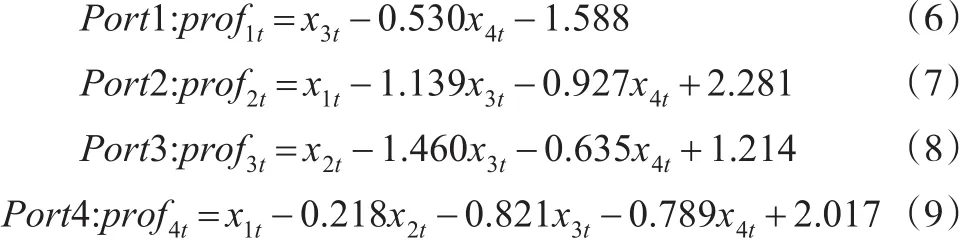
對每只股票將其樣本數據分為訓練集：2016.01.04-2017.04.05；測試集:2017.04.06-2017.07.06及預測集：2017.7.7-2017.9.29。運用混合神經網絡模型按前述給定的策略進行訓練、測試及預測。實驗中設定訓練次數為10000次，學習速率為0.0006，隱藏層為10層。通過上述訓練、測試，預測出2017年7月7日至2017年9月29日的各股票價格走勢，如圖1所示。

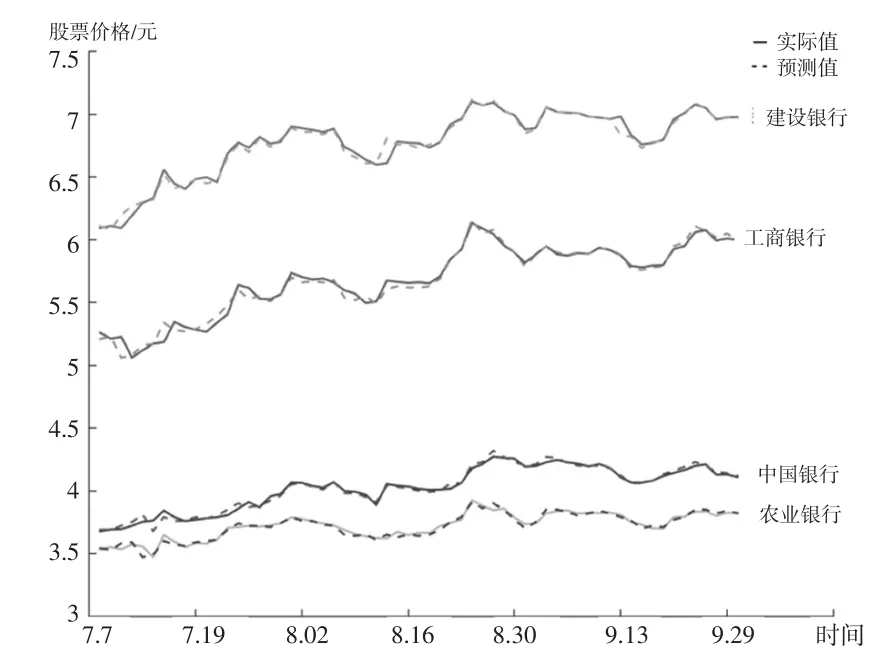
圖1混合神經網絡預測曲線與真實走勢曲線比較圖

再由式（6）至式（9）根據投資組合中各產品的權重計算出相應組合的利潤序列值profit。

在得到利潤序列{profit}后，建立其ARMA(1,1)模型，得到殘差項εit，之后按設定套利和平倉閾值并進行套利，由此完成統計套利的全過程。

具體交易策略。如對投資組合1即Port1，由式（6）：一份完整的多頭頭寸交易是買入0.53份中國銀行股票同時賣出1份農業銀行股票；一份完整的空頭頭寸交易則是賣出0.530份中國銀行股票同時買入1份農業銀行股票。同理，Port2、Port3和Port4中，各金融產品的投資比例由式（7）至式（9）確定，分別為：1∶-1.139;-0.927;1∶-1.460∶-0.635以及1∶-0.218∶-0.821∶-0.789。

其中，“-”代表反向操作，當然真正購買股票不存在小數，但這不影響交易策略的制定，因為可以同比例放大，使得交易比例為整數即可實現真正的套利方案。

3.4 套利交易結果

為比較BP、LSTM以及混合神經網絡模型預測套利的優劣，先采用BP神經網絡進行預測，發現預測平均誤差超過1%；然后采用LSTM神經網絡進行預測，預測平均誤差降低到0.7%左右；最后用混合神經網絡預測，平均誤差在0.5%左右。表3給出了基于BP神經網絡和混合神經網絡預測并進行套利結果（鑒于LSTM只在預測區間的前端誤差較大，總體套利結果只在前段與混合神經網絡模型套利結果出現差異，故此處省略）。

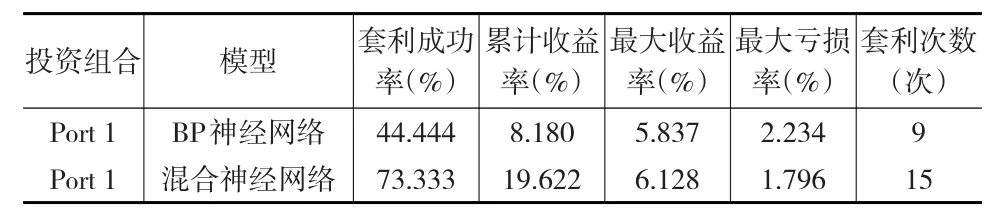
表3 Port1投資組合套利結果

從表3中可以發現，無論是從套利成功率、累計收益率、最大收益率，還是從最大虧損率和套利次數來看，混合神經網絡模型的套利結果均優于BP神經網絡模型的套利結果。由此可見，預測準確率是統計套利成功的重要保證。預測越準確，套利成功率、收益率和套利次數越高，同時最大虧損率下降，說明提高預測準確率可以顯著減少風險。

接下來本文探討在原有兩個組合中增加投資組合產品個數，再應用混合神經網絡模型和BP神經網絡模型進行統計套利會產生什么樣的結果。仍舊從套利成功率、累計收益率、最大收益率、最大虧損率和套利次數這幾個指標研究套利策略效果，結果見表4。

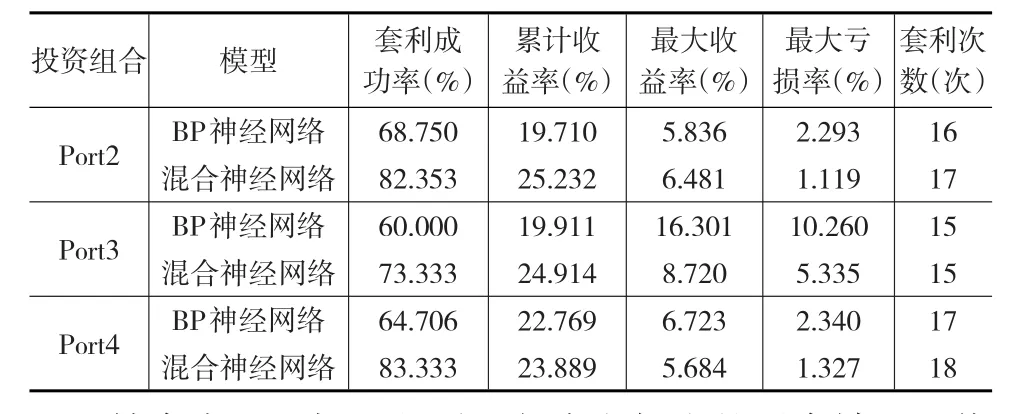
表4 投資組合Port2—Port4的兩種模型套利結果比較

結合表4和表3可以得到：本文提出的混合神經網絡模型的套利成功率及累計收益率均高于單一BP神經網絡模型的套利結果；增加投資組合中的產品數，即投資組合的多元化可以有效地增加套利成功率和累計收益率；基于混合神經網絡模型的最大虧損率低于單一BP神經網絡模型套利的最大虧損率。但從Port2—Port4的結果發現：基于混合神經網絡模型預測成功的套利次數與基于BP神經網絡模型預測成功的套利次數沒有顯著提高（但亦沒有減少）；特別是最大收益率指標，有的組合（如Port3）混合預測的結果低于BP神經網絡模型預測的結果。具體分析其原因發現：套利結果的好壞與投資組合中金融產品本身的優劣有較大的關系。事實上，Port2是在Port1的基礎上增加了工商銀行；Port3是在Port1的基礎上增加了建設銀行，經過查證，在此預測時間段內，工商銀行主營收入增長遠高于建設銀行。由此可見，在投資組合中增加產品，要審慎選擇。增加產品的好壞可能直接影響到統計套利的成功及獲利大小。怎樣審慎選擇一個投資組合？這正是下一步研究的問題。

4 結論

本文以LSTM神經網絡模型和BP神經網絡模型為基礎，提出了一個混合神經網絡模型，用于統計套利的預測，研究不同的投資組合下的統計套利策略，并用中、工、農、建四大國有銀行2016年1月1日至2017年9月30日的真實數據為樣本進行實證分析。結果顯示：本文提出的混合神經網絡模型的預測準確率明顯高于BP神經網絡的預測結果。帶來的直接效果就是使得套利收益率顯著提升，即采用本文提出的混合神經網絡的套利策略是十分有效的。不僅如此，混合神經網絡的套利成功率、套利次數均增加，最大收益率和最大虧損率均得到改善，因此采用混合神經網絡建立預測模型,并進行套利,會使預測更準確，套利更精準，收益也更大。之后投資組合的多元化檢驗，不僅同樣符合上述結論，也可以有效地增加套利次數和套利成功率，說明投資組合越多元，相對風險會更小，換言之套利機會越多。但并不是投資組合中的金融產品越多越好，只有對金融產品作合理篩選，包括數量和質量，才能獲得較好的投資收益。

研究中也存在不足，首先本文只選擇了四個公司做樣本進行研究，樣本較少可能存在一定的實驗誤差。其次，在統計套利收益的測算中，沒有考慮交易所產生的費用，如手續費等。當考慮相關費用，投資收益會有所下降，但是對整體實驗結果無較大影響。再次，以什么原則選擇一組投資組合產品，以獲得更多套利機會和更高收益？本文還沒有給出確定的方法。