基于接近性綜合關聯度的區間灰數的決策模型

席沙沙，魏 勇

（西華師范大學 數學與信息學院，四川 南充 637000）

0 引言

灰色關聯決策是灰色系統理論的重要組成部分，廣泛應用于社會、經濟的各個領域中。近年來，很多學者從不同的角度研究了多指標決策問題，取得了很大發展。對于具有區間灰數的多指標決策問題文獻[1]提出了灰色區間關聯系數公式，將經典灰色關聯決策由清晰數的情況推廣到了區間灰數的情況，建立了基于滿意度水平下的灰色區間關聯算法；文獻[2]提出了基于理想方案的最大關聯度方法、基于臨界方案的最小關聯度方法，以及同時考慮理想方案和臨界方案的綜合關聯度方法；文獻[3]提出了基于信息還原算子的區間灰數序列關聯度的計算方法，研究了具有區間灰數的多指標決策問題，建立了多指標區間灰數關聯決策模型；文獻[4]提出了區間灰數關聯決策方法，從而把灰色關聯分析理論由實數序列拓廣到區間數序列；文獻[5]通過引進區間數向量范數，對區間數多指標決策問題的決策矩陣進行規范化處理，在此基礎上給出了區間數多指標決策問題的灰關聯分析法；文獻[6]針對只有部分屬性權重信息且屬性值以區間數形成給出的不確定多屬性決策問題，提出了一種逼近理想關聯度的決策分析方法；文獻[7]提出了一種基于灰色關聯的區間評價方法；文獻[8]探討了決策方案的屬性值為區間灰數、屬性權重部分已知和決策者對方案有偏好的灰色決策問題。

文獻[9]利用信息分解法將區間灰數序列分解成兩個部分：一個為由區間左端點組成的“白部序列”，另一個為由區間長度組成的“灰部序列”。然后根據向量投影方法對正、負理想點的“白部”、“灰部”分別進行向量雙向投影，進而根據構建向量雙向投影的一次性決策模型。但是向量雙向投影的方法計算復雜，因此本文對文獻[9]的方法進行簡化：在區間灰數序列信息分解的基礎上，結合文獻[10]中的接近性關聯度，計算各區間灰數序列的“白部序列”、“灰部序列”與理想序列的接近性關聯度，最后通過比較接近性關聯度得出最好的方案。

1 基本概念與基本理論

定義1[11]：在灰色系統理論中，人們通常把只知道取值范圍而不知道其確切值的數稱為灰數。把既有下界aL又有上界aU的灰數稱為區間灰數，記為

通常，在多屬性決策中，有“效益型”屬性、“成本型”屬性等，且屬性不同的“量綱”也不同，因此需要把不同屬性的進行規范化處理，處理方法如下：

對于效益型序列，其區間灰數左右端點為：

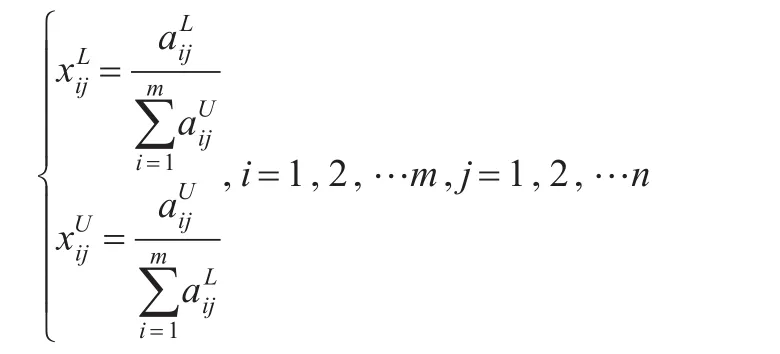
對于成本型序列，其區間灰數左右端點為：

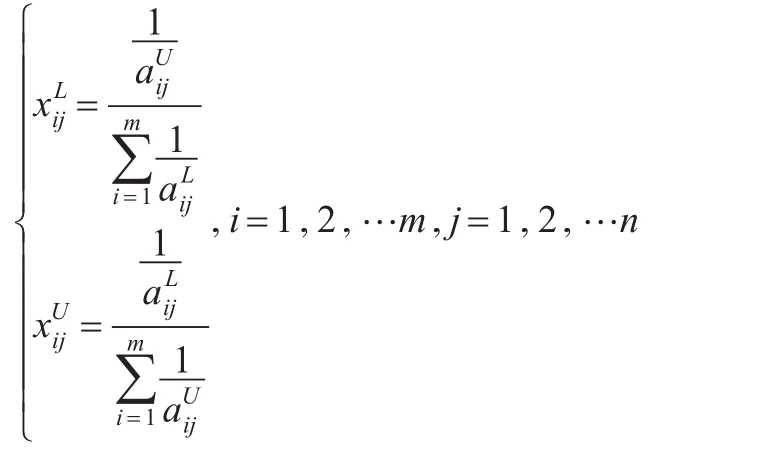
定義2[9]：設區間灰數序列為：

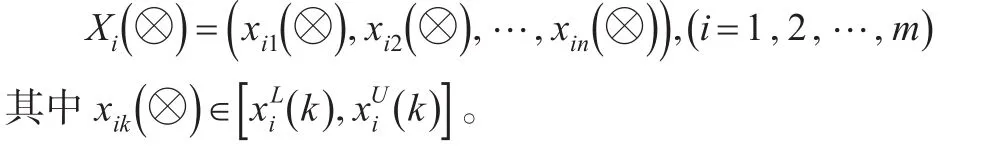
方案Xi與X+的“白部序列”的接近性關聯度為：

同理，方案Xi與X+的“灰部序列”的接近性關聯度為：

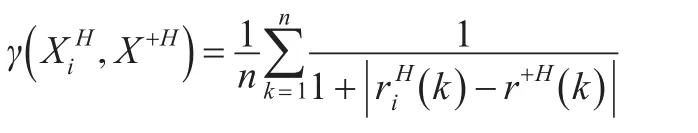
因此，方案Xi與X+的接近性綜合關聯度為：

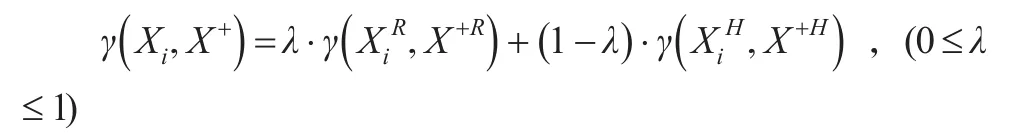
其中，權重一般取λ=0.5，當然也可根據具體情況斟酌確定λ。

對于在有部分權重信息的屬性值為區間灰數的情況下，接近性關聯度計算方法如下：

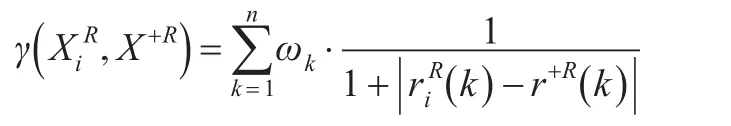
同理，方案Xi與X+的“灰部序列”的接近性關聯度為：

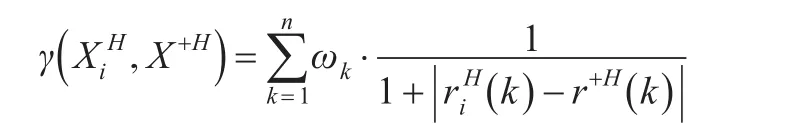
因此，方案Xi與X+的接近性綜合關聯度為：

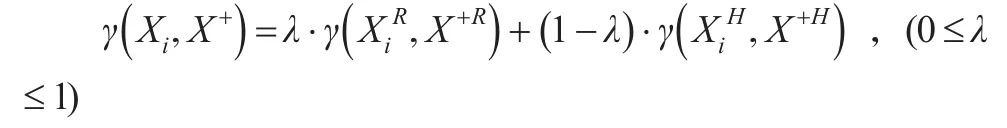
其中，權重一般取λ=0.5，當然也可根據具體情況斟酌確定λ。

2 算法步驟

第1步：構建區間灰數決策矩陣。

第2步：對區間灰數決策矩陣進行規范化處理。

第3步：構建理想方案。

第4步：利用信息分解法處理區間灰數。

第5步：計算各方案到理想方案的接近性綜合關聯度。（一般先分別計算各方案白部到理想方案白部的接近性綜合關聯度，灰部到理想方案灰部的接近性關聯度，再計算各方案到理想方案的接近性綜合關聯度）。

第6步：根據接近性關聯度進行方案排序。

3 應用實例

例1[9]：一家投資銀行打算投資一個項目，現有4家公司X1、X2、X3、X4較為合適。現選取投資凈產值率A1、投資利稅率A2、內部收益率A3、環境污染程度A4這4項指標對這4家公司進行評估，來確定最終決定是否進行投資。具體數據如表1所示：其中A1、A2、A3為效益型指標，A4為成本型指標。

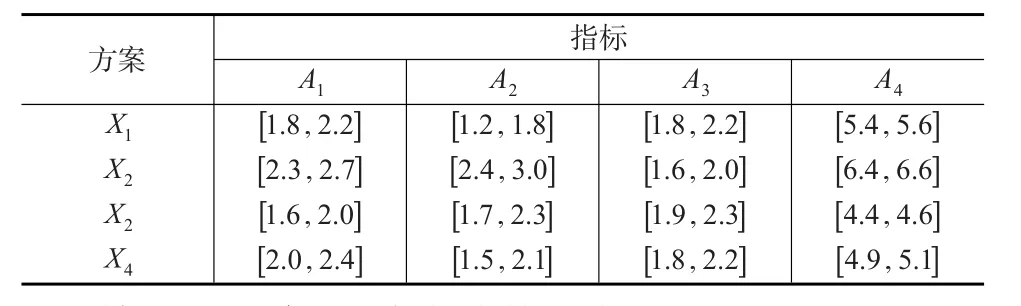
表1 區間灰數決策矩陣

第1步：構建區間灰數決策矩陣。

第2步：對區間灰數決策矩陣進行規范化處理（見表2）。

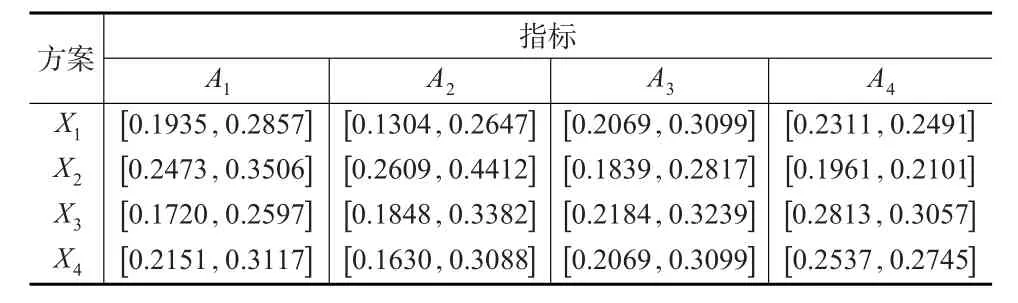
表2 規范化區間灰數決策矩陣

第3步：構建理想方案。

理想方案：

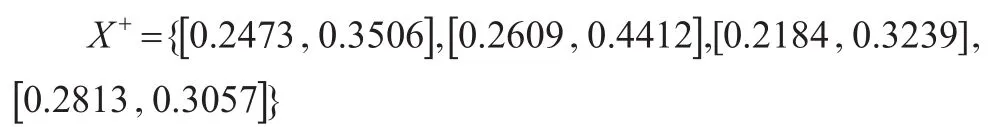
第4步：利用信息分解法處理區間灰數。

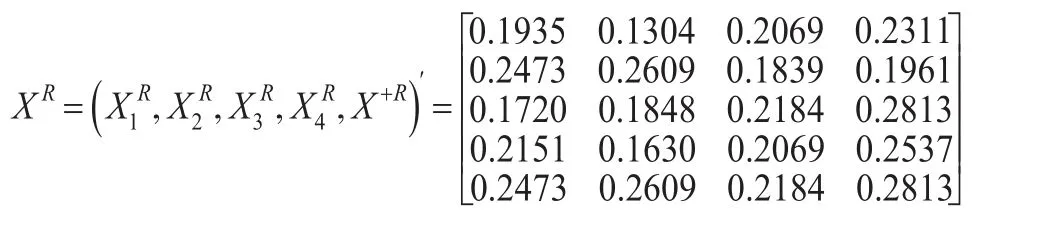
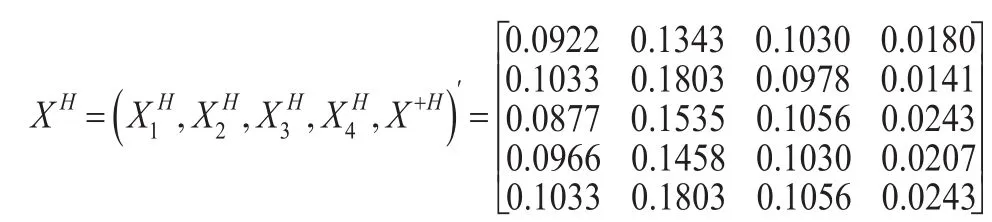
第5步：計算各方案到理想方案的接近性綜合關聯度。

接近性綜合關聯度又分三步完成：

①各方案與理想方案的“白部序列”的接近性關聯度：

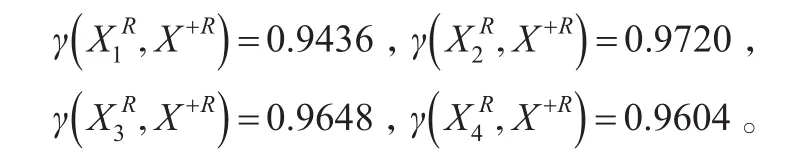
②各方案與理想方案的“灰部序列”的接近性關聯度：

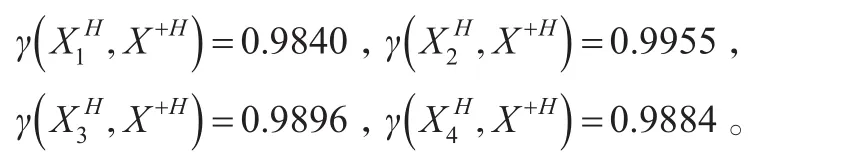
③各方案與理想方案的接近性綜合關聯度：對本例特殊情況而言各方案的“白部序列”與理想方案的“白部序列”接近程度，完全與各方案的“灰部序列”與理想方案的“灰部序列”接近程度排序一致，無論權重為何值，其綜合關聯度都會保持共同順序，所以沒有必要計算接近性綜合關聯度具體值，而直接進入下一步。

第6步：根據接近性關聯度進行方案排序。

而文獻[9]方案之間的排序也為X2＞X3＞X4＞X1，顯然本文的方法更簡單。文獻[9]運用了向量雙向投影的方法來構建模型，計算過程復雜；而本文考慮到越接近理想方案則方案越好，從而選用了灰色接近性關聯度來建模，且計算方法簡單。

例2[2]：某人打算購買一套房子，現有4類房屋X1、X2、X3、X4可供選擇。現選取房屋面積A1（m2）；設備A2（水平）；環境A3（水平）；價格A4（單位面積價格：元/m2）；距工作地點距離A5（公里）這5項指標對這4類房屋進行評估，來確定最終決定購買哪套房屋。具體數據如表3所示，其中A1、A2、A3為效益型指標，A4、A5為成本型指標。各指標權重為ω1=0.2087，ω2=0.2225，ω3=0.2256，ω4=0.2046，ω5=0.1386。

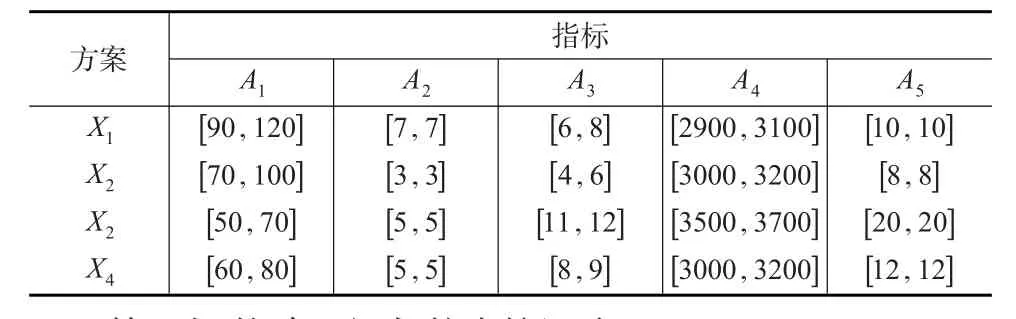
表3 區間灰數決策矩陣

第1步：構建區間灰數決策矩陣。

第2步：對區間灰數決策矩陣進行規范化處理（見表4）。

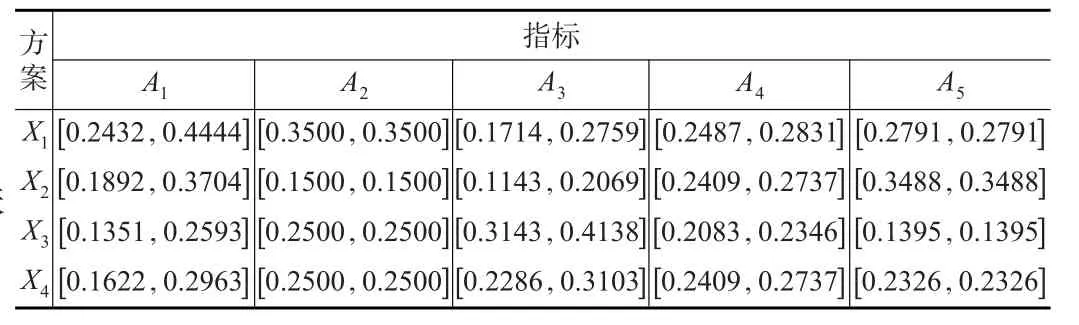
表4 規范化區間灰數決策矩陣

第3步：構建理想方案。

理想方案：

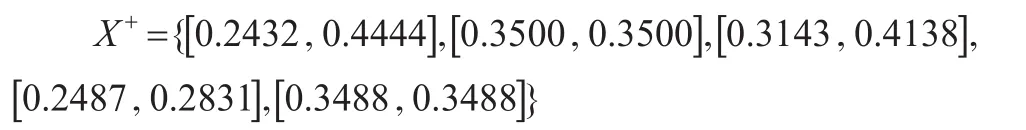
第4步：利用信息分解法處理區間灰數。

第5步：計算各方案到理想方案的接近性綜合關聯度。

接近性綜合關聯度又分三步完成：

①各方案與理想方案的“白部序列”的接近性關聯度：

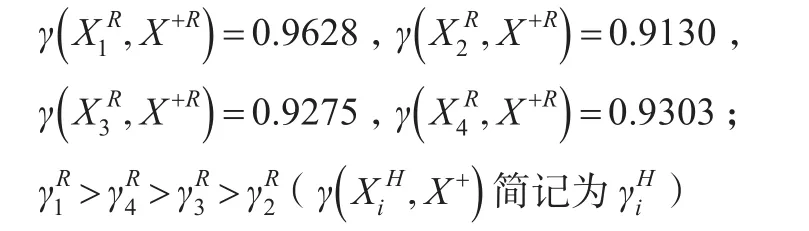
②各方案與理想方案的“灰部序列”的接近性關聯度：

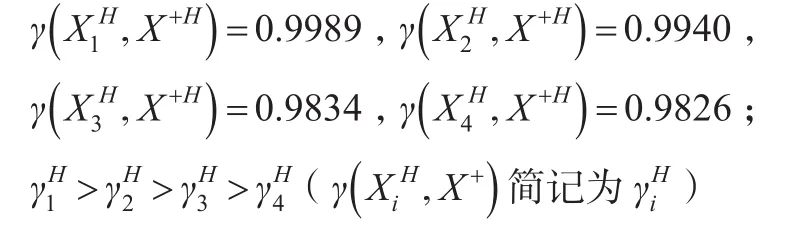
③各方案與理想方案的接近性綜合關聯度：

其實僅就尋找最優方案而言，無論是白部還是灰部都是方案是最接近，但方案2、3、4的排序差異較大，必須用綜合關聯度來權衡。

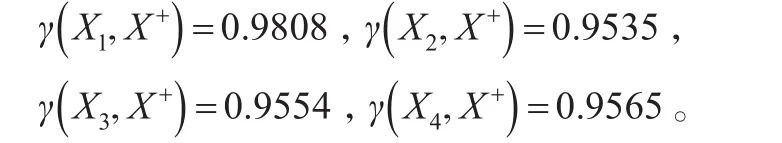
第6步：根據接近性綜合關聯度進行方案排序。

從計算結果上看出γ＞γ＞γ＞γ（γ(X，X+)簡記為

1432i γi）可知方案X1更接近理想方案，故方案之間的排序為X1＞X4＞X3＞X2，因此購買第X1套房子較好。

而文獻[2]方案之間的排序為X1＞X4＞X2＞X3，也是方案X1較好。文獻[2]同時考慮了理想方案和臨界方案的綜合關聯度方法。而本文考慮了理想方案的接近性關聯度的方法，顯然本文的方法更簡單。

4 結論

本文研究了決策矩陣為區間灰數的多目標決策問題，提出了將區間灰數序列分解為“白部序列”、“灰部序列”，然后分別計算出各方案與理想方案的“白部序列”、“灰部序列”的灰色接近性關聯度。

該方法計算簡便，具體體現在：

（1）對原始數據不作始點零象化、初值單位化、均值化等處理。避免了因這些處理抹殺數據之間的本質差異的可能性，比如，始點零像化會抹殺對應坐標相差一個常數的差異，初值單位化會抹殺相差常數倍的差異，等等不一一列舉，這將導致差異較大的方案關聯卻較大的可能性無法排除。順便指出：反映接近性的相關程度的關聯度不宜作數據初始化變換，反映相似性相關程度的關聯度必須將“作數據初始化變換不改變關聯度值”做為合理性要求。

（2）直接計算各方案與理想方案之間的接近性關聯度，沒有涉及投影的計算，盡管絕大部分情形方案投影越接近理想方案就是方案接近理想方案，但無法排除例外情形的存在，至少是缺乏嚴格的理論保證，本方法避免了可能導致例外情形的發生的擔憂。