網絡數據環境下動態抽樣框的構建及其應用

朱 鈺，王 恬

（西安財經大學a.統計學院；b.西安統計研究院，西安 710061）

0 引言

20世紀80年代由美國人提出“大數據”一詞，隨著信息技術和互聯網的不斷發展，“大數據”逐漸融入人們的日常生活、學習與工作。大數據的出現，無疑是給傳統的統計工作帶來了巨大的挑戰。2009年維克托·邁爾·舍恩伯格及肯尼斯·庫克耶在《大數據時代》一書中提出采用所有數據的方法（取代抽樣調查）。隨后，許多國內學者也紛紛在各大期刊上發表文章，并指出“大數據時代不需要抽樣”的觀點。而這種觀點無疑是將抽樣技術與大數據分割為獨立的個體來討論，是一種片面的理論認識。大數據理論是指盡最大可能收集與研究對象相關的“數據”（包括文檔、視頻、圖片等非結構化數據），通過數據處理技術進行分析，找尋研究對象與研究目的之間的關系，用以發現和解決問題的一種理論。《大數據時代》提出了三個最顯著的變化：一是樣本等于總體；二是不再追求精確性；三是相關分析比因果分析更重要。針對第一個顯著變化“樣本=總體”，給傳統的統計抽樣技術帶來巨大的挑戰——抽樣框確定，網絡數據滿足上述的“5V”特性，面對瞬時萬變、復雜多樣的數據環境，如何針對所要研究的問題，確定抽樣調查中的抽樣總體？如何將傳統的抽樣框變化為適應大數據時代下的抽樣框？這都是需要進一步研究和探索的問題。

本文將針對大數據給抽樣技術帶來的第一個挑戰——抽樣框變動問題進行深入地研究，從源頭上構建大數據背景下抽樣技術實施的基礎條件，為以后改進抽樣方法提供捷徑。

1 理論基礎

1.1 大數據的定義

在構建網絡數據環境下的動態抽樣框之前，先將文中提出的網絡數據環境所涉及的背景——大數據進行簡單的定義。

目前對大數據的定義還沒有形成統一的意見。麥肯錫全球研究院將大數據定義為：無法在一定時間內使用傳統數據庫軟件工具對其內容進行獲取、管理和處理的數據集合；維基百科將大數據定義為：所涉及的數據量規模巨大到無法通過人工，在合理時間內達到截取、管理、處理、并整理成為人類所能解讀的信息。針對不同專家對大數據的定義，根據統計學理論，本文對大數據的定義如下：

定義1：大數據（Big Data）是指所研究問題針對資料收集規模巨大、數據資料復雜等問題，無法通過傳統使用的工具、軟件在盡可能短的時間內實現數據的分類、處理、分析與存儲，需要用新的處理模式和流程優化能力來分析信息的集合。

網絡數據環境下動態抽樣框構建的主要核心是：動態抽樣框構建的理論支撐，由于目前這方面的研究甚少，所以本文就從抽樣的基本原理入手，結合網絡數據背景的特點，再融入抽樣框構建的關鍵來構建動態抽樣框。

1.2 抽樣原理

采樣過程所應遵循的規律，又稱取樣定理、抽樣定理。采樣定理說明采樣頻率與信號頻譜之間的關系，是連續信號離散化的基本依據。本文將在采樣定理深入理解的基礎上對抽樣技術中的抽樣原理進行定義，下面將從大數據背景下的動態抽樣框構建入手，對抽樣原理給出統計學方面的定義：

定義2：設所需要調查對象的目標總體是N，抽樣總體為M，調查總體為S；且對任意研究對象滿足如下條件：

利用一定的統計抽樣方法對滿足抽樣原則的對象進行篩選，最終達到利用調查總體S來估計抽樣總體M，并在此基礎上利用統計推斷理論來得到研究對象總體N的相關信息的方法稱之為抽樣原理。

上述三者總體之間的關系可由圖1表示：

圖1 N、M、S三者關系反映圖

在研究抽樣框之前，有必要對目標總體與抽樣總體之間的關系進一步說明：理想的狀態是抽樣總體應該與目標總體完全一致，也就是所有目標總體單元和抽樣總體單元完全是一一對應的關系。但在實踐中，兩者不一致的情況卻時有發生。就如圖1所展示的那樣，會存在未覆蓋的地方。同時，在調查中也會出現無應答的部分，使得調查總體與抽樣總體也不能一一對應。

定義3：（抽樣框）設由目標總體單元x1，x2，...，xN構成的目標總體為N，且抽樣單元s1，s2，...，sM構成抽樣總體是M（M?N），當滿足下面三個條件時稱抽樣總體M為抽樣框。

①目標總體單元xi(i=1，2，...，N)可以包含一個個體，也可以包含若干個個體；

②抽樣單元sj(j=1，2，...，M)可以包含一個個體，也可以包含若干個個體；

③sj?xi(i=j)

也就是說，抽樣框是抽樣總體的具體表現。通常，抽樣框M是一份含所有抽樣單元的名單，給每個抽樣單元編上號碼，就可以按照一定的隨機化程序進行抽樣；抽樣單元sj是構成抽樣框的基本要素（抽樣單元還可以分級）。一般意義上，好的抽樣框不僅與目標總體保持一致，而且還盡可能多的提供與研究的目標量有關的輔助信息，以便調查人員利用這些輔助信息搞好抽樣設計，提高抽樣估計效率。

抽樣框的設定與選擇不同對總體的估計也不同，也會出現抽樣框誤差，具體表現在：定義3中M∈N時、總體中單元數N不準確；上述兩種情況都會導致利用樣本統計量對總體參數進行估計就可能產生偏倚（誤差）。

1.3 相關理論

（1）大數定理：

設X1，X2，...，Xn是相互獨立且服從同一分布的隨機變量序列，對任意的i(i=1，2，...，n)有數學期望E(Xi)=μ；令隨機變量序列的任意n個單元的算術平均數為：

則對任意的ε＞0，有：

也就進一步說明抽樣過程中的樣本代替總體的原理，同時，大數定理說明了隨機事件的穩定性。特別地，當n→∞時，算術平均值與數學期望值μ就會越接近。即樣本量越大，其統計特性就會越接近總體的分布特征。

（2）極限定理：

設X1，X2，...，Xn是相互獨立且服從同一分布的隨機變量序列，對任意的i(i=1，2，...，n)有數學期望E(Xi)=μ、方差D(Xi)=σ2；令n個隨機變量之和為則有式（2）成立：

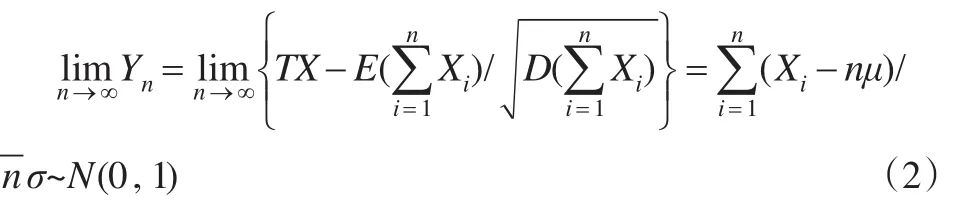
從式（2）表明，無論隨機變量序列服從什么分布，從中抽取n個樣本進行研究時，只要n足夠大，其樣本平均數就近似的服從數學期望為μ、方差為的正態分布，即明顯地，當n→∞ 時，抽樣誤差會越來越小，所以通過合理的抽樣方法一定可以獲得總體N的特征。

2 構建動態抽樣框的方法

傳統情況下抽樣框的建立方法與思路在上文已做了說明，但是，在大數據背景下，構建抽樣框的初始條件（總體N確定）難以滿足，這就對抽樣技術的研究提出了挑戰；且在大數據背景下不同時間段、相同時間段內滿足條件的進入總體的數據流是不定的（流速未定）。所以，下面將針對上述問題進行大數據背景下動態抽樣框的構建問題進一步加以說明：

2.1 動態抽樣框的定義

定義4：單位時間t=1s內數據流速為V(t)且t是一個服從一定條件的隨機變量，則在任意時間段Δti=tj-ti（j＞i）內的總體Nij滿足：

也就可以通過式（3）來定義動態抽樣框的總體Nij。顯然，Nij是一個時間ti，tj及流速V(t)代表單位時間流入的數據的個數，是不斷變化的量，即Nij就是時間ti→tj的數據總量，即抽樣框；隨著i，j的變化形成的動態總體，即動態抽樣框。動態抽樣框的構建過程可以用圖2加以說明：

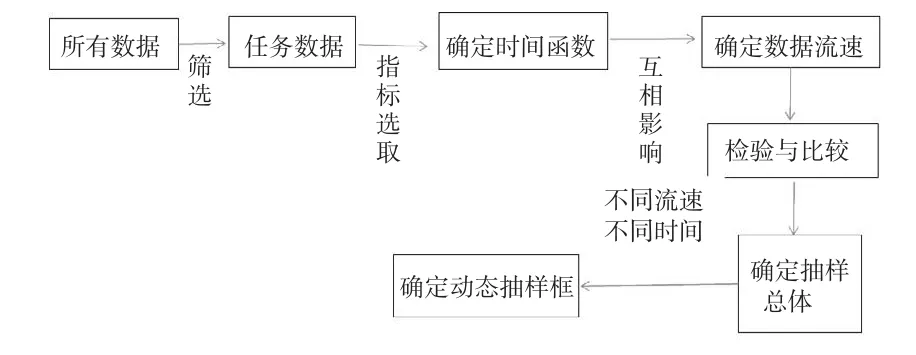
圖2 動態抽樣框構建的框架圖

2.2 動態抽樣框構建的具體步驟

（1）時間函數f(t)選擇

時間函數f(t)基于不同分段節點的選擇，基本原則是Ti≠Tj(i≠j，1，2，...，n)。但是由于大數據環境的復雜性，本文利用“重復等分”來確定時間節點函數f(t)。具體思路：

首先，確定研究問題的時間下限Tl和時間上限Td，即總體的時間段為[Tl，Td]；然后，在[Tl，Td]內按照隨機原則插入n1-1個點將總體分為n1個等間隔的時間段（間隔記為 Δt1），并利用n1來定義時間函數f1(t)=n1*Δt1；接著，在[Tl，Td]內按照隨機原則插入n2-1個點，將總體分為n2個等間隔的時間段（間隔記為Δt2），并利用n2來定義時間函數f2(t)=n2*Δt2；再接著，重復上述工作，可以得到m個fk(t)=nk*Δtk(k=1，2，...，m)的函數，要求n1≠n2≠...nm；最后，利用fk(t)(k=1，2，...，m)的總體變化情況確定最終時間函數f(t)，一般情況下時間總段是確定的值，即f(t)=c(常數)需要確定的是時間間隔函數Δti。

（2）流速V(t)的確定

在大數據背景下，數據的流速是瞬時萬變的，本文將借助“切割”的思想，通過數學歸納法、以時間函數f(t)為依據來確定速度V(t)的變換函數。具體思路：

首先，利用步驟（1）中對f(t)的定義將整個時間段劃分為n個小段，即T1=T2=...=Tn；然后，在T1中任取一個時間段(tv，ts)（滿足s＞v），并記錄T1左側tv時刻數據流入量為Vl(t1)、右側ts時刻流速為Vr(t1)；接著，在n-1個Ti(i=2，3，...，n)重復同樣的工作，可以得到Ti段的Vl(ti)，Vr(ti)；并將n組左右兩個時刻的流速Vl(ti)，Vr(ti)（i=1，2，...，n）進行描點畫線（找規律）；最后，為Vl(ti)，Vr(ti)擬合兩條函數曲線，并找出共性，確定最終的流速函數V(t)。

（3）抽樣總體N的確定

本文借助積分定理的思想，利用步驟（2）的結果將時間函數f(t)進行確定，并利用步驟（1）中的結果對流速V(t)進行確定，并在此基礎上通過“切割”與“重組”的思想對抽樣總體N通過求和進行確定。

3 隨機模擬

假定本文研究的時間段為2017年3月1日12:00至2017年3月31日12:00為期30天，也就是Tl=2017/03/01，Td=2017/03/31，且起止時間點均為12:00。

3.1 時間函數的定義

首先確定時間函數。根據需要，假定時間函數的等間隔Δti服從如下規律（也可實際情況進行規律找尋），即Δt1=20，Δt2=1/21，Δt3=1/22...，Δtn=1/2n。關 于fi(t)=ni*Δti的部分圖如圖3(a)和圖3(b)，圖3(c)為的關系圖（時間長度不變）。

圖3 時間間隔Δti和間隔數ni的關系圖

3.2 流速的確定

假定n=30，則T1=T2=...=T30=1天，按照計算機模擬的隨機原則對時間段內的時間節點進行選擇。1天=24小時，按照數據流入時間點的特性，本文用正態分布的隨機數來代替在每個Ti(1=1，2，...，30)內所選取時間“小時”的節點，再利用泊松分布產生的隨機數來確定所取時間“分鐘”的節點，最后，利用均勻分布的隨機數來確定時間“秒”的節點（具體程序略）。按照上述的過程在R中生成的數據表及對應的Ti時間點選擇如表1所示：

表1 時間函數選擇結果

從表1對時間點進行對號入座，即T1段內選取的時間是1點48分38秒至2點36分20秒，T2為2點36分20秒至2點48分40秒，T3為2點48分50秒至2點54分03秒……

由于在時間段內每個時間點的數據流入量V(ti)難以確定，所以按照上文的論述只需對每個時間段Ti的所選時間的左右端點進行測量即可。在此，本文假定時間段的左右兩邊數據的流入量是隨機的，在不假定分布的情況下，利用多種分布的隨機數的混合數來進行模擬所得結果如下：

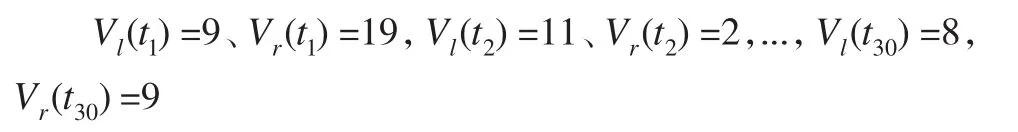
利用所得數據進行圖形展示，圖4（a）是全部流速數據的變化趨勢圖，圖4（b）和圖4（c）分別是左、右端點流速變化圖，具體如下所示：

圖4 流速變化圖

從圖4（a）不難看出在95%的置信度下流速V(t)的變化區間，本文由于模擬結果比較集中，故首先選取流速的均值9作為流速的勻速值，即此刻對研究的抽樣框進行計算如下：

接著，按照每個小階段的計算均值對抽樣框進行計算如下：

對上述兩種結果進行比較發現，二者之間計算出來的樣本框的總量差距并不大，因此可以根據自身所要研究的對象對方法進行選擇。

4 總結

本文根據大數據理論研究，對“大數據時代不需要抽樣技術”的觀點進行否定。針對大數據背景下抽樣技術面臨的三大挑戰，給出了解決最基本問題——抽樣框變動問題的方法，從抽樣原理出發來分析背景不同所帶來的抽樣框變動的規律，進而提出構建動態抽樣框的思想，并從理論和實例分析方面對大數據背景下的動態抽樣框的構建進行詳細說明。

不足之處在于，針對動態抽樣框的構建僅僅給出時間總段函數假定不變，數據流入隨機的抽樣框的模擬計算，沒有深入地將其他假定條件下的樣本框進行構建。且僅給出動態抽樣框的構建，沒有對大數據背景下抽樣方法的改進與應用進行討論，這將是日后的研究方向。