基于模糊包含度的貝葉斯粗糙集模型

魏 玲，張琬林，李 陽

（哈爾濱理工大學 經濟與管理學院，哈爾濱 150040）

0 引言

波蘭學者Pawlak于1982年提出的粗糙集理論是用來剖析不定性及不完整性的有效方法，可以從不完備信息中挖掘隱含知識以及潛在規律[1]。Pawlak粗糙集作為處理不確定與不精確問題的新方法，近年來迅速應用在數據挖掘和人工智能等領域，但其存在一定局限性，要求分析的類別一定是全部準確或肯定，即“包含”或“不包含”，不考慮某種程度上的“包含”或“屬于”[2]。為解決其容錯性能差這一缺陷問題，Ziarko于1993年對其進行了推廣改進，引入容錯關系提出變精度粗糙集模型[3]。在經典粗糙集模型基礎上，允許在對集合進行劃分時存在一定的錯誤分辨率以提高容錯能力，當前已有大量研究成果[4-6]。在實際應用中，理想的解決方案只需根據得到的信息去處理問題，不受預先給定參數的限制，且選取不同的參數會產生不同的決策規則。為克服這種約束，Slezak等引入貝葉斯理論提出了貝葉斯粗糙集模型[7]。

由于傳統粗糙集的應用對象是一般二元等價關系的信息系統，不適用自然界中的模糊信息系統，因此部分學者指出在模糊信息系統中應用粗糙集理論，最具有代表性的是Dubois等提出的模糊粗糙集模型[8]，但該模型也易受到噪聲數據的干擾。為克服傳統粗糙集的各種不同程度的缺陷，故將變精度粗糙集與模糊粗糙集二者相結合對學者來說具有重要研究價值。主要有以下兩個研究方面：一是采用模糊理論將變精度粗糙集進行一定程度的模糊化。做出杰出貢獻的學者主要有Mieszkowicz-Rolka[9]等。他在分別定義一種模糊包含集和一種錯誤包含度的基礎上，進而將上下近似算子生成變精度模糊粗糙集（VPFRS）模型進行了重新定義；二是使模糊粗糙集精度化，主要研究學者有王麗[10]等。

本文研究發現對這類推廣生成的VPFRS模型中參數的確定還有待改進。因此在VPFRS模型的基礎上，引入先驗概率來代替參數，提出一種基于模糊包含度的貝葉斯粗糙集（IDB-BRS）模型，也可稱其為貝葉斯模糊粗糙集，進而研究了模型的基本性質和單調性，并以屬性的相對重要度作為啟發式信息，給出了基于該模型的屬性約簡算法。最后通過驗證以上兩種模型的屬性約簡結果，證明IDB-BRS屬性約簡是合理有效的。

1 理論基礎

1.1 變精度粗糙集模型

定義1[3]：設S=(U,A,V,f)是一個信息系統，U為非空有限論域；A=C?D，C?D=?，C為條件屬性集，D為決策屬性集；V是屬性值的集合；f:U×A→V指研究對象的每一個屬性值都存在于其所對應的相應屬性之上。設X，Y為U的非空子集。如果對于每一個x∈X都有x∈Y則稱X包含于Y中，記作X?Y。令：為X相對于Y的可信度閥值，稱為X被Y包含的程度大小。

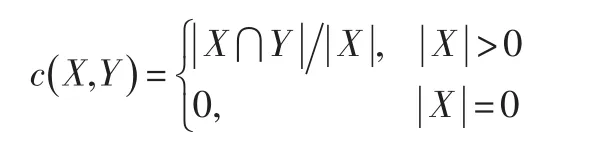
設(U,R)是近似空間，U為非空有限集合，R為U上對應的相關等價關系

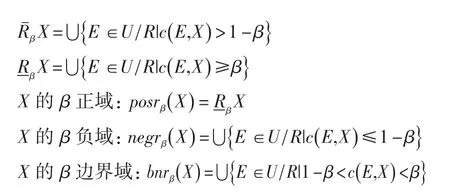
1.2 貝葉斯粗糙集模型

在屬性約簡等實際應用中，變精度粗糙集模型中參數值的選取受決策人主觀因素影響，缺乏合理性依據。因此有學者提出貝葉斯粗糙集模型，引入先驗概率替代參數，對獲取的信息進行高效處理[7]。

在信息系統S內，相對于X?U來說,E是U的相應等價關系，那么貝葉斯正域、負域、邊界域分別是：

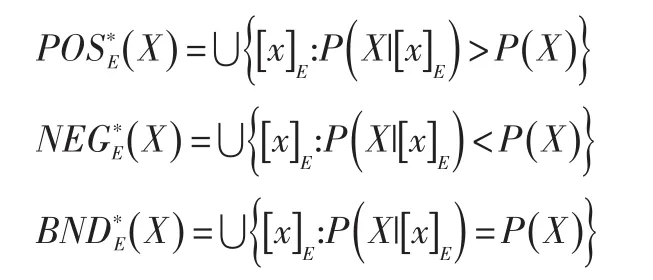
2 IDB-BRS模型及屬性約簡

2.1 模型構建

定義3：設U是有限非空集合，I=[0,1]，?是任意蘊涵，稱映射D:F(U)×F(U)→I為模糊包含度，其中I?A,B∈F(U)。

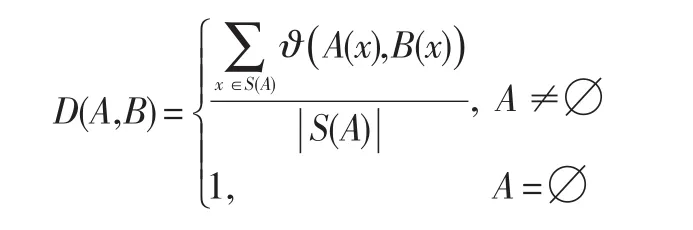
稱D(A,B)為A關于B的?模糊包含度。其中?選取為模糊集A的支集。

定義4：IDB-BRS模型：設U為有限非空論域，其中φ={C1,C2,…,Ck}為U的模糊覆蓋之一，也是U相對于C（ii=1,2,…,k）的劃分，D為模糊包含度，那么將稱作模糊包含近似空間。?X∈F(U)取那么X有關于E依的下近似以及上近似就是定義于U上的一對模糊子集：

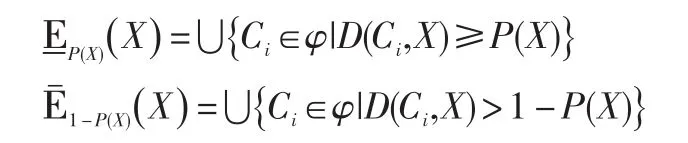
IDB-BRS模型的正域，邊界域和負域依次定義為：

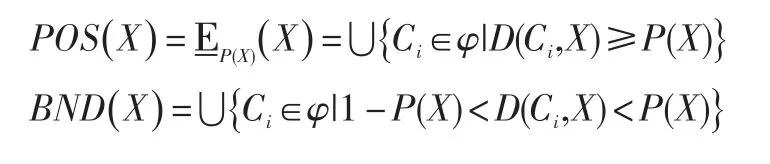
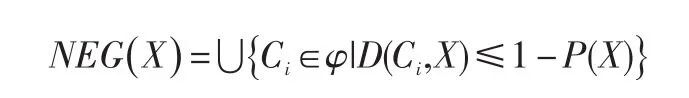
2.2 模型性質

性質1：設?是任意蘊涵，Ε=(F(U),φ,D)是模糊包含近似空間，那么在?X∈F(U)中，X相對于Ε依P(X)=的 下 近 似和上近似滿足條件

證明：由定義顯然。

性質2：設?是任意蘊涵，且滿足對于?x＞0，有成立為模糊包含近似空間，取且則有成立。

證明：由已知條件可得，?Ci∈φ，x∈S(Ci)，有?(Ci(x),0)=0成立，從而故又由性質1可得因此成立。

性質3：設?是任意蘊涵，且滿足對于?x∈I，有?(x,1)=1成立，Ε=(F(U),φ,D)為模糊包含近似空間，…,r且則有成立。

性質4：設?是右單調蘊涵，Ε=(F(U),φ,D)是模糊包含近似空間，那么在內條件下，A,B對于Ε依的下近似及上近似滿足下列性質：

性質5：設?是右單調蘊涵模糊包含近似空間，在條件下，A,B的交與并關于的下近似和上近似滿足如下性質：

性質6：設?是滿足邊界條件的左單調蘊涵，1-P(X)＜P(X)≤a內，a關于Ε依是模糊包含近似空間，在的下近似和上近似有成立。

2.3 屬性約簡算法

屬性約簡為粗糙集理論不可或缺的重要應用[11-14]，利用IDB-BRS模型對模糊決策信息系統進行相應屬性約簡后給出相應屬性約簡理論以及相關算法，并利用相關實驗數據對貝葉斯模糊粗糙集屬性約簡算法合理性與有效性進行相關驗證。

定義5：設S=(U,A,V,f)為模糊決策信息系統，U={x1,x2,…,xn}。模糊屬性集B={b1,b2,…,bm}，B?A,則關于B的相似度為其中，xi,xj看作是B上的模糊集，xik表示xi在模糊屬性bk下的隸屬度，RB簡稱為B的模糊相似關系。xi的相似類簡記為，稱為由模糊相似關系RB或由屬性集B誘導的模糊信息粒。

定義6：設S=(U,A,V,f)是模糊決策信息系統，其中U={x1,x2,…,xn}，A=C?D，C是條件屬性集，D是決策屬性集，B?C，RB,RD分別是屬性集B,D的模糊相似關系，那么記其中是U的模糊覆蓋，DF是U上的模糊集包含度，稱Ε=(F(U),φ,D)是 模 糊 包 含 近 似 空 間 ，?X∈F(U)取那么D有關于B的下近似分布以及上近似分布分別是：

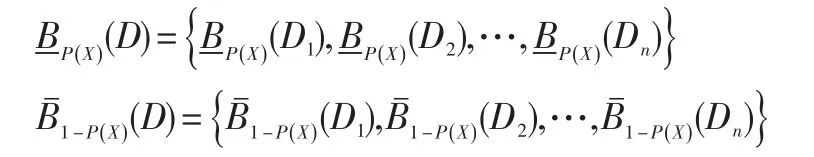
定義7：定義U為非空論域，U={x1,x2,…,xn}，Ε=為模糊包含近似空間,A,B∈F(U)，那么則是模糊集A與B之間的分離度，且 0≤ρ(A,B)≤1。

下面利用分離度定義屬性間相對重要度。

定義8：定義S=(U,A,V,f)是一個模糊決策信息系統，A=C?D，C是條件屬性集，D是決策屬性集，B?C，ρ則是分離度那么b∈B在B中相對于模糊決策屬性集D的P(X)重要度就為則c∈C在C中相對于D的P(X)重要度為則b∈C-B關于B相對于D的P(X)重要度為C內全部相對于D的ε精度P(X)的必須屬性全體，可以稱作C相對于D的ε精度核，為coreP(X)(C,D,ε)。

定義9：設S=(U,A,V,f)是一模糊決策信息系統，其中A=C?D，C是條件屬性集，D是決策屬性集，B?C，0≤ε＜1若B滿足：

則稱B是C相對于D的ε精度近似約簡。

屬性約簡為NP問題，所以不可以直接用定義對系統進行相應屬性約簡。下面利用屬性相對重要度給出IDB-BRS模型的屬性約簡啟發式算法。

算法：IDB-BRS模型屬性約簡算法

輸入：模糊決策信息系統

S=(U,A=C?D,V,f)，模糊包含度DF，參數ε；

輸出：S的一個相對約簡red。

步驟1：隨機選取c∈C，計算模糊相似關系Rc，RD；

步驟2：c→red；

步驟3：for任意ci∈C-red

計算sigi=sigP2(X)(ci,red,D)；

end

步驟4：選擇屬性cq滿足

步驟5：if屬性cq的重要度sigq＞ε

cq?red→red；

返回步驟3

else

輸出red

End

為增大搜索到最小約簡的概率，步驟1采用隨機搜索，且在步驟4中，當選擇屬性cq時，若出現一個以上的屬性滿足時，也采用隨機搜索來降低產生局部最優解的風險。在IDB-BRS屬性約簡算法中時間復雜度主要由步驟3和步驟4共同來決定，步驟3的時間復雜度為O(|C||U|2)，步驟4為O(|C|2|U|2)，因此，可知算法總體的時間復雜度為O(|C|2|U|2)。

3 實驗及結果分析

為驗證IDB-BRS屬性約簡具備合理有效性，將算法約簡后的數據結果與文獻[10]中的VPFRS生成的結果對比分析，得出結論。

3.1 實例分析

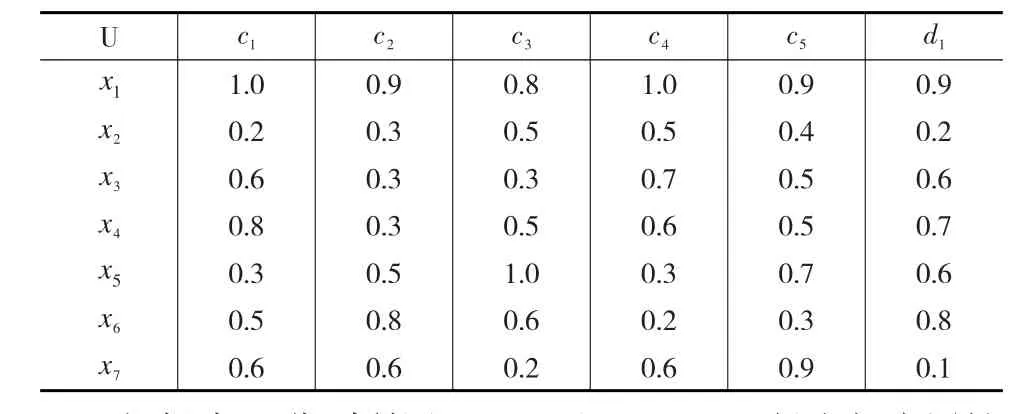
表1 模糊決策信息系統

根據表1，分別利用VPFRS和IDB-BRS得出相應屬性約簡結果。在VPFRS中，對參數β及ε取不同值得出的相應約簡結果見表2。其中，“/”前面的數值表示500次循環后得到的所有約簡中所包含的平均屬性個數，“/”后面的數值表示在進行500次循環后得到最小約簡所包含的屬性個數。

在IDB-BRS屬性約簡算法中，沒有參數的限制影響，約簡結果只與ε精度的取值有關，根據公式，由實驗數據可得出為實現與VPFRS約簡結果對比的條件統一性，精度ε取相同的變化值，約簡循環次數為500次，約簡結果如表3所示。

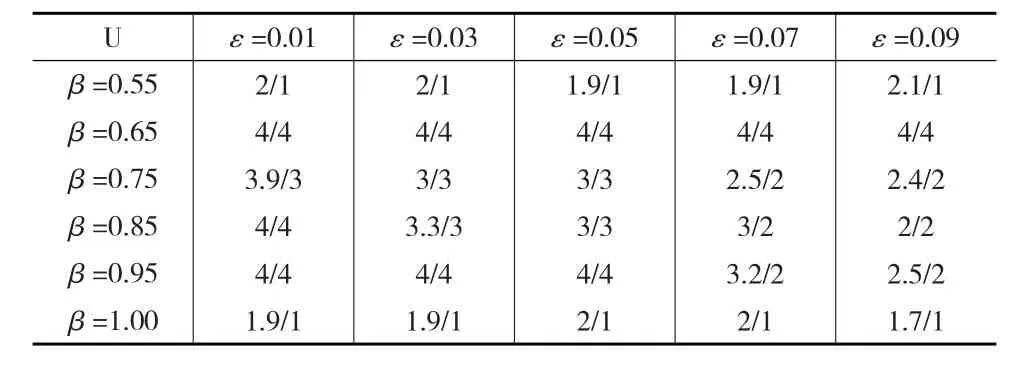
表2 約簡結果

表3 約簡結果

由實驗數據可看出，在IDB-BRS屬性約簡算法中，當P(X)=0.71時，在不同精度下得出屬性個數比與在VPFRS屬性約簡算法中β=0.75時對應不同的精度得出的屬性個數比結果相一致。下面比較通過約簡得到的候選解項是否存在相同交集。

設B?C是由約簡算法得到的C相對于D的ε精度約簡的候選解，則稱為B的質量，其中γB(D)為γB(D)對D的支持度。在VPFRS模型約簡結果中，當參數β=0.75，ε=0.05時，B1={c1,c2,c3}為模糊信息系統屬性約簡的一個候選解。可以求得B1的D正域為對D的支持度為0.8795。C的D正域對D的支持度為得出B1的質量為0.9835。在IDB-BRS模型約簡結果中，當ε=0.05時，對應得到的候選解為同理，根據公式算出B2的質量為經過對比，可得出結論候選解項具有相同交集，說明企業在進行供應鏈合作伙伴選擇時傾向于交貨運輸質量高且企業技術狀況良好的對象。經過實例分析可以證明得到IDB-BRS屬性約簡算法具備相應合理性。

3.2 UCI數據集測試

為更進一步檢驗IDB-BRS屬性約簡算法具備一定程度的有效性，選擇3組UCI中常用的數據集（Soybean、Credit、Balance）來對本文提出的屬性約簡算法以及文獻[10]中的VPFRS屬性約簡算法進行相關比較分析。Soybean數據集包括4個決策類，35個屬性個數，樣本數為307；Credit數據集包括2個決策類，15個屬性個數，樣本數為690；Balance數據集包括4個決策類，4個屬性個數，其中樣本數為625；在計算屬性約簡時，參數ε在區間[0.03,0.07]里選取比較合理，否則，過大會引起過度約簡，過小會起不到約簡的作用。因此，實驗測試時取參數ε=0.05。由于VPFRS受參數的影響，為克服經驗主義，從0.5到1之間等距離選取6組β值來進行實驗。本次實驗運行的硬件環境為Intel處理器，3.50GHz，2.00GB內存；軟件環境為Windows7&MATLAB R2012a。

使用IDB-BRS屬性約簡算法（以下簡稱算法1）和文獻[10]VPFRS屬性約簡算法（以下簡稱算法2）分別對3組數據集進行相應屬性約簡，同時記錄其屬性約簡結果與約簡運行時間，并將得到的數據集作為SVM分類器的輸入，根據10折交叉驗證方法輸出識別結果。實驗結果見表4。

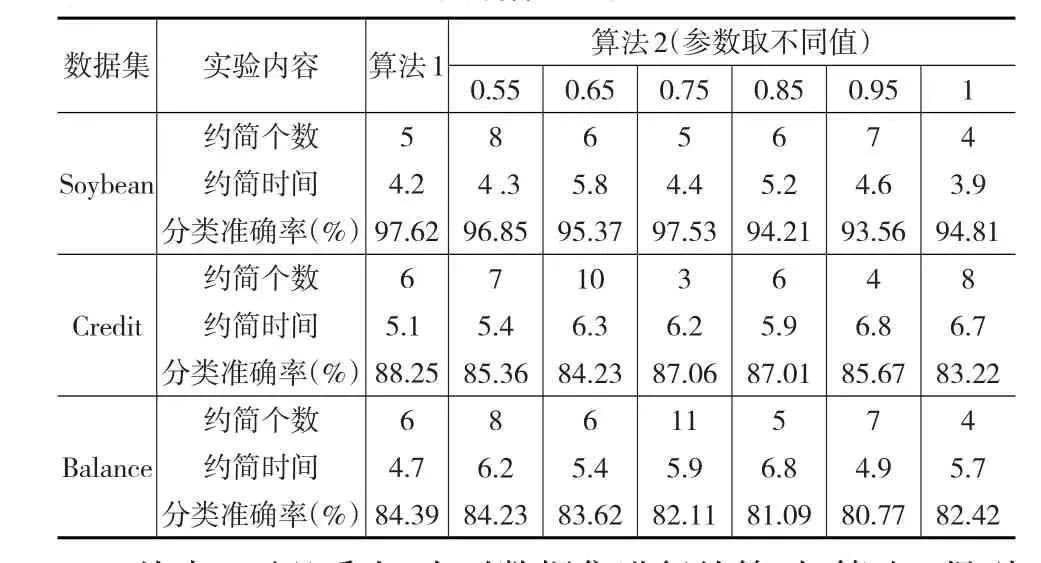
表4 兩種約簡算法結果對比

從表4可以看出：在對數據集進行約簡時，算法1得到約簡個數在算法2取不同參數值得到的約簡結果范圍內，說明IDB-BRS模型屬性約簡算法是VPFRS在參數互不相同條件下所獲得的屬性約簡的一種情況，它具備合理性。在對比分類準確率時發現算法1優于算法2，同時，由于不受參數的限制，在約簡時間上也低于算法1的約簡時間。綜合以上數據分析，實驗結果表明基于IDB-BRS的屬性約簡算法具備合理與有效性，且它相對于變精度模糊粗糙集而言不需要預先給定參數，在知識獲取屬性約簡方面有實際應用價值和意義。

4 結論

由于考慮到VPFRS模型存在一定約束條件，故根據貝葉斯粗糙集和變精度粗糙集理論研究，運用先驗概率替換參數推導出基于模糊包含度的貝葉斯粗糙集模型，并同時在模糊決策信息系統進行屬性約簡過程中運用此模型。經過對UCI數據集進行一系列實驗證明此模型屬性約簡算法合理、有效。基于模糊包含度的貝葉斯粗糙集模型是變精度模糊粗糙集模型無參數化的高級推廣方式之一，在未來實際應用中對其性質以及其屬性約簡算法的改進還有待進一步探究。