基于同倫方法的地月系L2點小推力轉移軌道優化

潘 迅，泮斌峰

(西北工業大學航天學院，西安 710072)

1 引言

在地月系三體模型中，L2點在地月連線上，且始終位于月球背面，不僅可以作為月球探測和深空探測的中轉站，還可以在L2點建立月球觀測站，實時監測月球背面情況，為月球背面著陸提供相關信息[1]。我國的嫦娥五號再入返回飛行試驗器的服務艙曾于2014年11月28日到達地月系L2點，并在2015年1月4日離開L2轉移至環月軌道[2-3]。

嫦娥五號再入返回試驗器利用化學發動機經過多脈沖機動完成軌道轉移，轉移過程較為簡單，所需時間較短。然而，隨著推進技術的發展，電推進、等離子推進等持續小推力推進方式由于具有比沖大、控制精度高等優點，能極大地提高探測器的有效載荷的比重[4]，因此將在未來的航天任務，特別是深空探測任務中，扮演越來越重要的角色。

由于小推力發動機的推力幅值小，持續時間長，完成轉移所需的軌道圈數多，在轉移過程中初始狀態量對轉移軌道有較大影響，即對初始值很敏感，因此優化過程存在較大困難。此外，相比于傳統的二體模型，限制性三體問題的非線性更強，導致該小推力轉移軌道優化問題的求解難度增加。小推力轉移軌道優化方法主要可以分為直接法、間接法和混合法[4]。直接法通過將狀態量和控制量進行離散，將軌道優化問題轉化為非線性規劃問題，直接對離散參數進行尋解[5-6]；間接法基于最優控制理論的經典變分法推導得到最優控制的一階必要條件，將其轉換為兩點邊值問題，通過數值方法對該兩點邊值問題進行求解，從而得到轉移軌道[7-8]；混合法只利用間接法推導得到的最優控制律，但不包含其他最優性條件，通過參數優化方法進行求解[9]。其中，間接法由于利用了最優性條件，可以保證所得解的局部最優性，且計算精度高。然而間接法將軌道優化問題轉換成兩點邊值問題后，雖然理論上可以利用打靶法對該問題直接求解，但由于作為優化變量的協態變量沒有物理意義，且算法的收斂域較小，因此，對于推力值小、轉移圈數多的問題，求解過程存在很大困難。

為了增加優化算法的收斂域，降低求解難度，同倫方法被廣泛應用于軌道優化。同倫方法，是指從較簡單問題出發，通過改變同倫參數，求解對應的一系列子問題，最終得到原問題的解。其在小推力在轉移軌道中的應用主要有兩個方向：一是針對燃料最優問題，通過對性能指標進行同倫，先求解連續光滑控制問題，然后通過同倫迭代，最終得到不連續的Bang-Bang控制的燃料最優轉移軌道[10-11]；二是針對推力很小的軌道優化問題，先求解較簡單的大推力值對應的軌道優化問題，然后通過對推力幅值進行同倫，逐漸減小推力幅值，最終得到所需的很小推力幅值的轉移軌道[12-13]。

目前對限制性三體問題中的小推力轉移軌道優化問題研究較少，Caillau等[12]對從航天器從GEO軌道到地月系L1點和月球軌道的轉移軌道進行相關研究，本文將其擴展到了航天器從地球GEO軌道到地月系L2點的時間最優轉移軌道優化問題。首先基于最優控制理論，將地月系三體問題模型下的小推力轉移軌道問題轉換為兩點邊值問題，然后結合同倫方法對該兩點邊值問題進行求解。

2 動力學模型

考慮航天器同時受到地球引力和月球引力，忽略地球非球形攝動、太陽引力、太陽光壓等其他攝動，并假設月球圍繞地球的運行軌道為圓軌道，則可用圓限制性三體問題來描述航天器的運動。僅考慮航天器在月球軌道面內的平面運動，并且忽略轉移過程中航天器的質量變化，則航天器在旋轉坐標系下的動力學模型為式(1)～(2)：

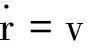
(1)

(2)

式中：r=[x,y]T和v=[vx,vy]T分別為航天器的位置矢量和速度矢量，m0為航天器初始質量，Tmax為航天器可以提供的最大推力，u為轉移過程中的實際推力大小，α=[αx,αy]T為單位推力方向。則可定義航天器有效勢能函數U如式(3)，g(r)和h(v)分別表示為式(4)、(5)：

(3)

(4)

h(v)=[2vy,-2vx]T

(5)

需要注意的是，在動力學模型式(1)～(2)中，各變量均為單位化后的值，其中長度歸一化單位為1 DU=3.8440×105km，時間歸一化單位為1 TU=3.75676967×105s，質量歸一化單位為1 MU=M0kg(M0為航天器實際質量)。歸一化后，地球在旋轉坐標系的位置為(-μ,0)，月球的位置為(1-μ,0)。

本文針對航天器從地球GEO軌道到L2平動點的時間最優小推力轉移軌道進行研究。在初始時刻t0，航天器在GEO軌道上的位置自由，其狀態量可以表示為式(6)：

x0=[r0cosθ0-μ,r0sinθ0,-v0sinθ0,v0cosθ0]T

(6)

時間最優問題的性能指標可以表示為式(7)：

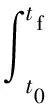
(7)

時間最優小推力轉移軌道優化問題的本質，就是在滿足初始狀態約束式(6)和終端狀態約束xf的條件下，通過優化變量u和α，使性能指標最小。根據龐德里亞金極小值原理，引入拉格朗日乘子，構造哈密爾頓函數為式(8)：

(8)

式中：λr=[λx,λy]T和λv=[λvx,λvy]T也稱為協態變量，其微分方程為式(9)～(10)：

(9)

(10)

為使哈密爾頓函數為極小值，從式(8)可知，推力大小和推力方向的最優控制律應為式(11)～(12)：

u*=1

(11)

(12)

對于航天器初始時刻的狀態量x0，由于存在優化變量θ0，需要對橫截條件進行推導。根據最優控制理論，可以得到對應的橫截條件為式(13)：

(x0+μ)λy0-y0λx0+vx0λvy0-vy0λvx0=0

(13)

對于時間最優問題，轉移時間自由，對應的橫截條件為式(14)：

H(tf)=0

(14)

至此，將最優控制問題轉換為兩點邊值問題，其初始時刻的狀態值由式(6)確定，終端時刻的約束包括狀態約束xf和橫截條件式(13)～(14)。該兩點邊值問題可利用打靶法進行求解，打靶函數表示為式(15)：

F(y)=O

(15)

式中y=[θ0,λx0,λy0,λvx0,λvy0,tf]T為優化變量。

3 推力幅值的同倫方法

將時間最優小推力轉移軌道優化問題轉換為兩點邊值問題后，雖然理論上可以利用打靶法對式(15)進行求解得到優化變量y的值，再對初值進行積分得到轉移軌道。然而推力越小，轉移時間越長，轉移圈數越多，打靶過程對初始猜測值就越敏感，打靶的收斂域就越小。此外，相比于傳統的只考慮中心引力場的二體模型，限制性三體模型的非線性更強，從而增加了求解難度。因此，為了克服小推力轉移軌道優化問題的初始值敏感問題，本文利用同倫方法進行求解。

3.1 構造同倫函數

基于所需求解的原問題，構造容易求解的問題作為同倫初始問題，而同倫過程中具有全局收斂性，因此同倫方法可以有效增大打靶過程收斂域，減小求解難度。同倫函數的一般構造形式可以表示為式(16)：

H(y,κ)=κF(y)+(1-κ)G(y)

(16)

式中：y∈n為優化變量，κ為同倫參數，F:n→n和G:n→n均為光滑的映射函數，分別表示所需求解的原問題和構造的同倫初始問題，H:n×→n為構造得到的同倫函數。根據初始問題G的不同，一般可以將同倫方法劃分為牛頓同倫(Newton Homotopy)，定點同倫(Fixed-point Homotopy)和尺度不變仿射同倫(Scale-invariant Affine Homotopy)[14]。針對本文的時間最優小推力轉移軌道優化問題，在推力幅值中引入同倫參數κ，構造的同倫函數的動力學模型為式(17)～(18)：

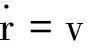
(17)

(18)

式中：TL?Tmax為足夠大的推力值，在該推力值下，轉移軌道優化問題較容易直接求解，Tmax為所需求解問題的實際推力幅值。對應于式(16)中的一般同倫形式，F為所需求解的推力值為Tmax的原問題，G為容易求解的推力值為TL的初始同倫問題。在時間最優的性能指標下，得到的哈密爾頓函數為式(19)：

(19)

協態變量的微分方程保持式(9)～(10)的形式不變，同時最優推力大小u*和最優推力方向α*和式(11)～(12)保持一致。邊界約束條件和橫截條件也與原問題保持不變。至此，同倫問題轉換成一系列隨著κ值變化的兩點邊值問題，通過求解這一系列的同倫子問題，最終可得到原問題的解。

3.2 同倫曲線跟蹤方法

同倫方法除了構造合理的同倫函數，還需要選取合適的同倫曲線跟蹤方法。同倫曲線的跟蹤方法主要可以分為離散同倫和連續同倫。離散同倫可以描述為，將同倫參數從0到1劃分為m個離散節點，即0=κ1<κ2<…<κm-1<κm=1，先求解κ1對應的初始問題的解，然后將得到的解y1作為κ2對應的同倫子問題的初始猜測值，求解得到該問題的解y2，然后再將y2作為κ3對應的子問題的初始猜測值，依次計算，最終得到κm對應的原問題的解ym[7]。離散同倫簡單直觀，但若相鄰兩個κ節點之間距離較遠，則以前一個節點的解作為當前節點子問題的猜測值時收斂性不能保證；更重要的是，當同倫曲線存在拐點時，離散同倫將在拐點處失效。

本文利用連續同倫中的偽弧長法跟蹤同倫路徑[15]。不同于離散同倫根據同倫參數κ來選取同倫節點，偽弧長法沿著同倫曲線的切線方程，根據偽弧長的步長Δs進行迭代計算。偽弧長法是一種預測-校正方法。首先在當前節點計算表征梯度信息的雅克比矩陣，將步長Δs分配到各個優化變量上，得到下一個節點的信息，然后再利用牛頓法等校正方法對下一個節點的值進行修正，從而得到該節點所對應的解[15]。如圖1所示，假設在第i個節點，(κi,yi)為非線性方程組H(κ,y)=O的已知解，定義該點處的單位切向量為式(20)：

(20)

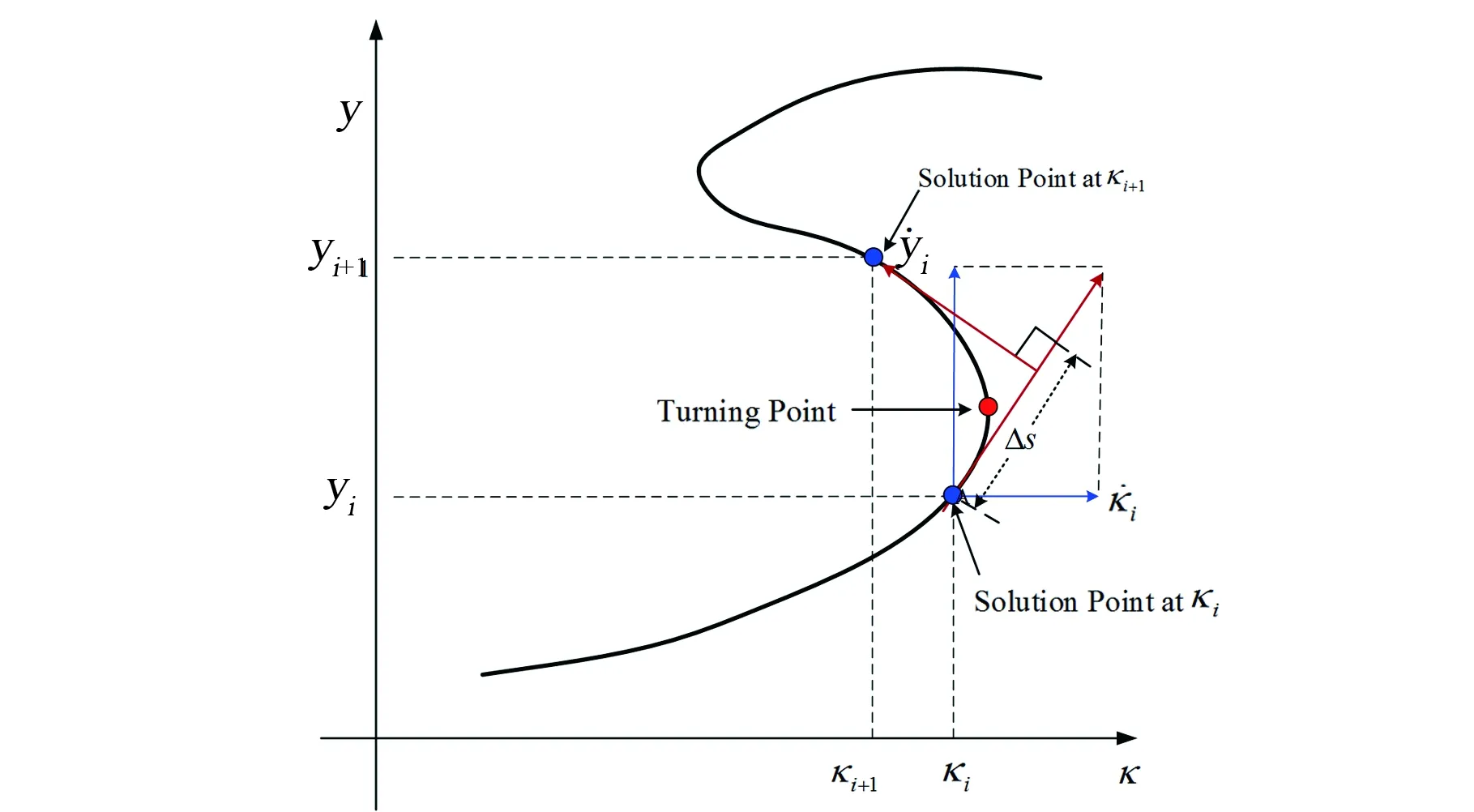
圖1 偽弧長法示意圖Fig.1 Geometric interpretation of pseudo arclength continuation method

(21)

H(κ,y)=O

(22)

由于κ值的變化方向由同倫曲線的切線方法確定，在同倫過程中κ可以增加，也可以減小，因此可以用于跟蹤存在拐點的同倫路徑。

4 數值仿真驗證

本文的仿真算例為地月系平面限制性三體問題下航天器從GEO軌道到L2的時間最優小推力轉移軌道，航天器的初始質量為1500 kg，發動機最大推力值為Tmax=1 N，對應的初始推重比為6.8027×10-5。航天器初始位置由式(6)確定，終端狀態約束為航天器終端時刻狀態量與L2點重合，GEO軌道半徑為r0=0.109689855932071 DU，航天器在GEO軌道上的初始速度為v0=3.000969693845573 DU/TU。

首先選取較大的推力值為TL=10 N，此時利用打靶法，可得初始問題的解為y0=[-7.4762,-3.7986,6.9355,-0.3092,-0.0844,1.4413]T。對應的轉移軌道如圖2所示，其中藍色實心圓點表示地球位置，紅色實心圓點表示月球位置，航天器到達L2點所需的轉移軌道圈數為1圈。

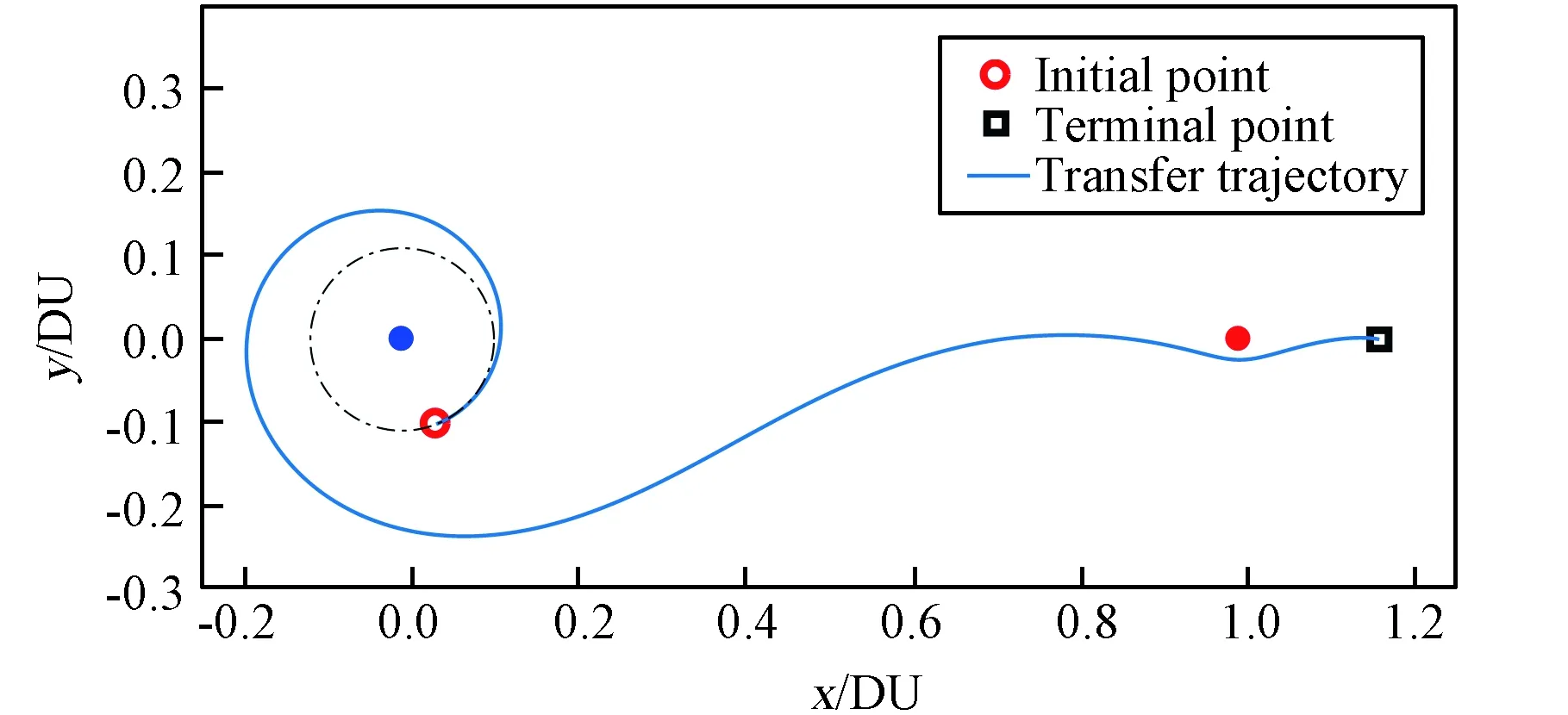
圖2 TL=10 N時從GEO到L2點的轉移軌道Fig.2 Transfer trajectory from GEO to L2 libration point with TL=10 N

以初始解y0為同倫初始點，利用偽弧長法跟蹤同倫軌跡，可以得到從κ=0到κ=1的同倫路徑，其中優化變量中的轉移時間tf的同倫路徑如圖3所示，初始時刻的協態變量λ0=[λx0,λy0,λvx0,λvy0]T如圖4所示，表示初始時刻航天器在GEO軌道上的位置的變量θ0的同倫曲線如圖5所示。從圖中可以看出，該同倫曲線并不是隨著κ單調遞增的，而是存在多個拐點。在同倫初始階段，κ值沿著同倫路徑增加，但同倫曲線在κ=0.8588時遇到第一個拐點，改變了同倫路徑的方向，使κ值沿著同倫路徑減小，直到在κ=0.8408時遇到第二個拐點，使κ值重新沿著同倫路徑增加，如此往復，直到同倫路徑到達κ=1，最終得到Tmax=1 N的轉移軌道。

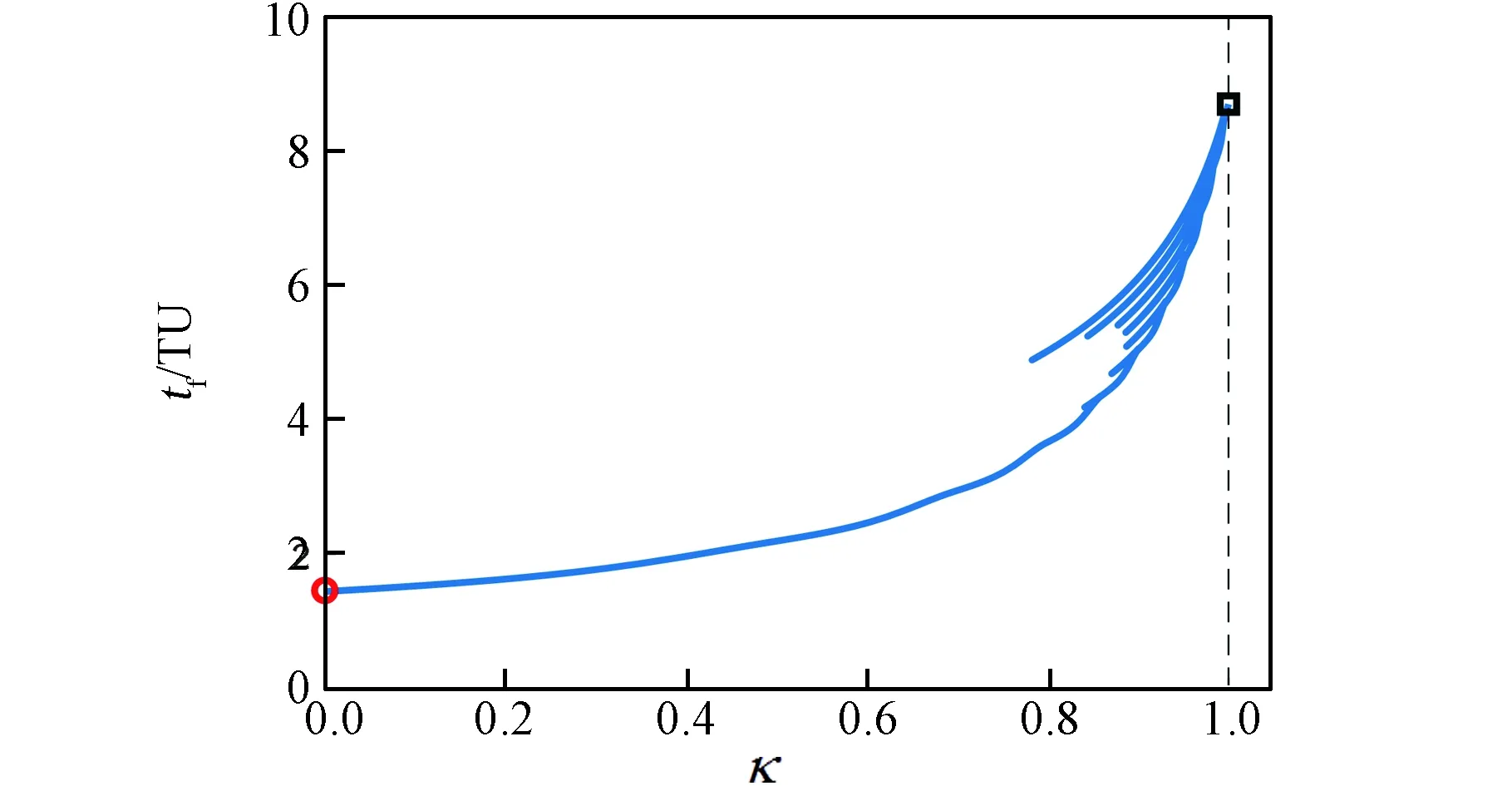
圖3 轉移時間tf的同倫曲線Fig.3 Homotopy curve of the transfer time tf(κ)

圖4 初始時刻協態變量λ0的同倫曲線Fig.4 Homotopy curves of costate λ0(κ)

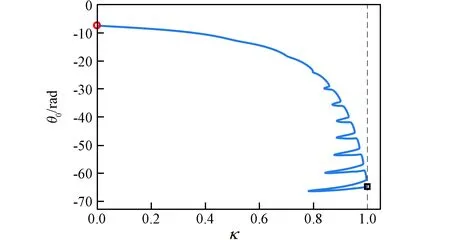
圖5 表示航天器在GEO上的位置的θ0的同倫曲線Fig.5 Homotopy curve of θ0(κ)

值得注意的是，同倫路徑上的每一個點都對應該點κ值下的一個解，即在對應推力值下，滿足打靶方程的一條時間最優轉移軌道。這是因為間接法的最優控制律和橫截條件是基于一階最優性條件推到得到的，可以保證滿足這些約束條件的解至少是極值點，即局部最優解，但不能保證是全局最優解。而在軌道轉移優化問題中，特別是轉移圈數較多的問題，一般都存在多個局部最優解。從同倫曲線中可以看出，在第二個拐點κ=0.8408之后，每個κ值對應的推力下都存在多個解。以κ=0.90為例，其對應的推力值為1.9 N，在這條同倫路徑中共存在13個解，對應的轉移時間范圍為5.0480～ 6.1190 TU，通過對性能指標即轉移時間進行對比，即可在這些局部最優解中選取得到最優解。對于原問題中的Tmax=1 N的轉移軌道，雖然在這條同倫路徑中只存在1個局部解，但可以預見的是，如果繼續跟蹤同倫路勁，隨著同倫過程的進行，將會得到更多的局部解。根據tf的同倫路徑的變化規律，當前得到的這個解，對應的轉移時間將始終小于其他解，即可認為當前得到的解是最優解。

從圖5中可知，與圖2對應的10 N時的轉移軌道相比，Tmax=1 N的轉移圈數增加了9圈。該解對應的轉移軌道如圖6所示，所需轉移時間為8.7113 DU，即37.8777天。轉移過程中航天器發動機的推力幅值始終保持最大值1 N，推力方向α*的變化情況如圖7所示。

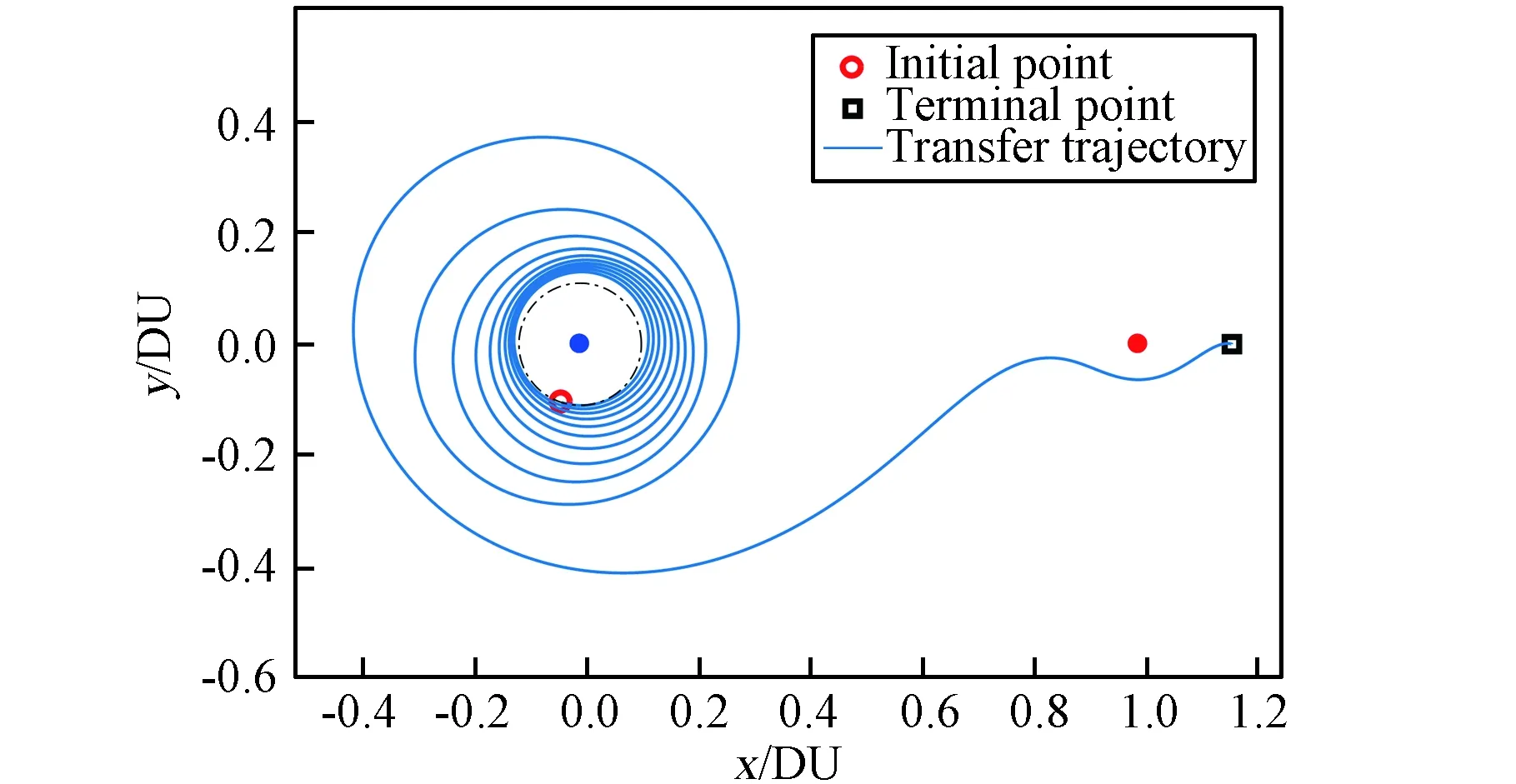
圖6 Tmax=1 N時的從GEO到L2點的轉移軌道Fig.6 Transfer trajectory from GEO to L2 libration point with Tmax=1 N

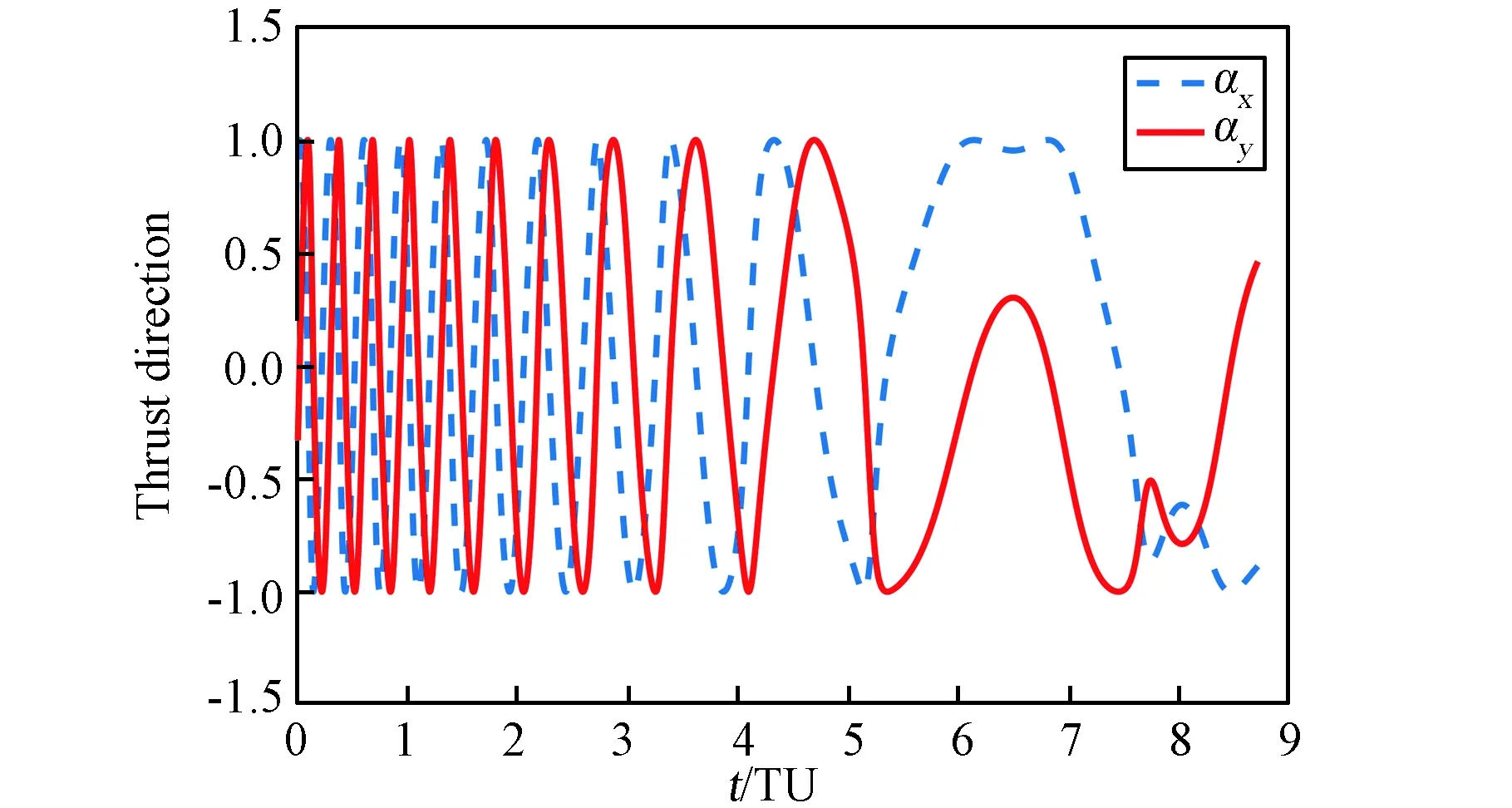
圖7 Tmax=1 N的轉移軌道推力方向α*隨時間的變化曲線Fig.7 Variation of thrust direction α* along the transfer trajectory with Tmax=1 N

5 結論

1) 在轉移軌道優化問題中，針對推力大小進行同倫時，同倫曲線存在拐點，離散同倫不能得到完整的同倫曲線，因此需要選取連續同倫軌跡跟蹤方法，利用偽弧長法可以跟蹤得到連續同倫路徑，得到包括拐點在內的完整同倫信息，有利于對同倫過程及同倫結果進行分析；

2) 對于多圈的小推力轉移軌道優化問題，可能存在多個滿足最優性一階必要條件的局部最優解，需要對性能指標進行對比才能確定最優解。若直接對小推力轉移軌道進行求解，并得到其中一個解，不能從該解本身判斷其是否為全局最優解，但如果利用連續同倫法跟蹤完整同倫路徑得到小推力轉移軌道，則可以依據該解在同倫路徑的位置及同倫路徑變化規律來判斷該解是否為全局最優解。