帶工期指派的產品服務系統訂單隨機調度問題研究
張 楊,但 斌,高華麗
(1.重慶大學經濟與工商管理學院,重慶 400044;2.重慶大學現代物流重慶市重點實驗室,重慶 400030;3.西南政法大學管理學院,重慶 401120)
1 引言
隨著市場競爭日益激烈和產品利潤空間不斷壓縮,傳統制造業開始由生產型制造向服務型制造轉變。2016年7月,國家工信部、發改委、中國工程院聯合印發了《發展服務型制造專項行動指南》[1],指出:“(制造企業)從單純出售產品向出售‘產品+服務’轉變,有利于延伸和提升價值鏈,提高全要素生產率、產品附加值和市場占有率”。這種“產品+服務”的整體解決方案又被稱為產品服務系統(Product service system,PSS)[2]。為了按期交付產品與服務,服務型制造企業需要為客戶的PSS訂單制定有效的調度方案并指派合理的工期,否則就會因訂單延遲交付而受到誤工懲罰,甚至導致客戶流失[3]。然而,在PSS的交付過程中,生產時間與服務時間可能具有隨機性。例如,電梯供貨與安裝合同常常包含定制化需求,無法得到電梯生產與安裝過程中每一道工序的精確時間,而只能結合現場操作和根據以往類似產品的生產與安裝經驗進行估計。這種隨機性使得PSS訂單調度與工期指派問題變得更為復雜。因此,在生產與服務時間均具有隨機性的條件下,如何聯合制定有效的PSS訂單調度與工期指派策略是服務型制造企業亟待解決的現實問題。
目前,在PSS運營管理領域,尚缺乏針對PSS訂單調度或工期指派問題的研究文獻,而現有的PSS運營管理的定量研究主要有兩類:企業宏觀層面上的PSS運營策略制定和微觀層面上的生產與服務任務運作計劃。大多數文獻從宏觀角度探討了如何制定企業的PSS運營策略,如產品和服務的定價策略、契約機制設計和能力配置等等。例如,Tsay和Agrawal[4]考慮由一個制造商和兩個零售商組成的產品服務供應鏈,研究了零售商競爭環境下產品價格和服務水平的動態決策問題;Lee等[5]通過研究傳統渠道與服務化渠道存在競爭時制造企業的最優定價與質量決策問題,發現當產品對服務的依賴性較高或渠道競爭較激烈時,制造企業實施服務化更有利;Xie Wenming等[6]在信息不對稱條件下對比分析了產品服務供應鏈的三種契約設計,結果表明契約實施的有效性很大程度上受供應鏈權力結構與成本信息類型的影響;劉宇熹和謝家平[7]針對租賃PSS研究了節約共享契約對協調再制造企業與客戶利益的重要作用;Xie Wenming等[8]以確保供應鏈中制造商和服務商間的充分信息共享為目標,探討了如何有效規劃產能和實現多渠道分銷;Li Gang等[9]分析了零售商自建與外購服務能力決策對產品服務供應鏈成員績效的影響,發現服務外包能夠提高零售商的服務水平并降低制造商的批發價格;姚樹俊和陳菊紅[10]考慮由兩個制造商和一個零售商組成的產品服務供應鏈,以制造商提供服務為視角,研究了不同權利結構下制造商的服務能力決策問題。以上文獻側重于如何通過增加企業或供應鏈的收益來提高利潤,因此未對成本控制策略作深入探討。僅有少數文獻從企業執行層面對PSS運作過程的最優控制策略進行了研究。例如,Li Na和Jiang Zhibin[11]針對帶有額外服務能力和不耐煩顧客的生產服務系統構建了分塊Markov最優控制模型;Wang Kangzhou等[12]針對同時銷售產品和PSS的服務型制造企業提出了最優生產與需求準入控制策略。但此類文獻均假設對PSS需求按照簡單的先來先服務規則進行調度,未對更為現實且有效的復雜調度策略作深入探討和分析,而這正是本文的主要研究內容。
另一個與本文相關的研究領域是調度管理。早期,學者們主要針對生產調度[13-15]或服務調度[16-17]問題開展研究;后來,為了進一步提升MTO(make to order)型制造企業的運營效率和降低其運營成本,一些學者開始研究產品生產與配送服務的聯合調度問題。例如,Garcia和Lozano[18]考慮帶有時間窗的生產與配送調度問題,以最大化訂單利潤為目標構建了整數規劃模型,并提出求解問題的禁忌搜索算法;Li等[19]針對消費類電子產品供應鏈研究了裝配生產與空運的協同調度問題;Low等[20]以最小化最大完工時間為目標構建了時間窗約束下的生產與配送調度模型,并基于遺傳算法設計了求解問題的啟發式算法;馬士華和呂飛[21]在隨機需求條件下構建了基于Supply Hub的供應鏈生產與配送協同決策模型。上述研究中,產品和配送服務之間不具有嚴格的匹配與集成關系:同一客戶訂單的產品在數量較多時可由不同運輸工具分批或分時段配送,同一運輸工具也可以同時為多個客戶提供配送服務,并且配送所需時間與選擇的運輸工具或運輸路線相關,而非與產品本身相關。而PSS訂單中的產品與服務具有高度集成性和匹配性:產品與服務往往是一一對應的關系,不同類型的產品對應的服務在服務方式和服務時間等方面不一致,且服務時間通常與產品的復雜性或客戶需求相關。例如,不同型號電梯的生產與安裝時間一般不同,且安裝時間與客戶的戶型和層高等要求有關;而在電梯安裝過程中,同一電梯安裝隊在同一時間只能為一臺電梯提供安裝服務。因此,以往針對生產與配送服務的調度方案不能適用于PSS訂單調度問題,需要基于PSS的運作特點研究新的生產與服務集成調度策略。
鑒于此,本文考慮生產時間與服務時間的隨機性影響,以最小化訂單提前、誤工和工期指派費用的期望總和為目標研究服務型制造企業的PSS訂單調度與工期指派聯合決策問題,并探討問題的解決方案,以期為服務型制造企業的PSS訂單調度管理提供有價值的啟示。
2 問題描述與基本模型
2.1 問題描述與假設
考慮由一個制造工廠和n個區域服務中心組成的服務型制造企業,如圖1所示。企業通過區域服務中心收集該地區客戶的PSS訂單需求,各訂單所需產品由制造工廠集中進行生產,產品完工后運送到客戶處并由相應的區域服務中心提供所需服務,從而最終完成PSS的交付。上述服務型制造企業在現實中很常見,如許多品牌電梯廠商在中國建立了電梯制造基地并在各省區設立分公司(負責該省區的電梯銷售、安裝和維保等業務)。在計劃期的初始時刻,區域服務中心i(i=1,2,…,n)收到一個PSS訂單(記為訂單oi),其中訂單oi由一單位產品與相應服務組成(如一臺電梯的生產與安裝合同)。各區域服務中心的訂單構成了企業需要處理的一組確定訂單集合O={o1,o2,…,on}。企業需要為每個訂單指派工期并制定訂單調度計劃。其中訂單oi的工期由兩部分組成:產品工期dpi(同時也是服務交付期的開始時間)和服務交付期長度lsi(即服務交付期的截止時間dsi與產品工期dpi的差值,lsi=dsi-dpi)。例如,電梯設備生產安裝合同通常會在條款中分別對電梯的交貨期與安裝工期進行規定。為了制定最優的訂單調度與工期計劃,企業需考慮在訂單交付過程中可能產生的各項生產與服務費用。如果訂單oi的生產在服務交付期的開始時間之前完工,產品將在庫存中等待,每單位時間產生的庫存費用為hi;如果訂單oi的生產誤工或服務延遲交付,則企業每超期一單位時間需支付給客戶的誤工費用為bi;此外,由于較長的工期可能會使企業喪失訂單,進而損害企業的競爭力[22],故參照以往有關產品訂單工期指派問題的研究[13],本文考慮訂單oi每單位時間的工期時長會產生潛在的懲罰費用ai。由于各訂單的收益在最初與客戶談判時就已確定,不會隨訂單調度計劃而改變,因此為了實現利潤最大化的目標,管理者需要聯合決策訂單序列和工期以使所有訂單的期望費用總和最小。

圖1 服務型制造企業運作示意圖
為了方便研究,本文假設:制造工廠在同一時刻只能生產一個PSS訂單的產品;各服務中心在產品到貨后能夠立即開始提供服務;生產時間和服務時間均是隨機的和相互獨立的,且服從已知正態分布;準備時間和運輸時間包含在生產時間中;生產任務和服務任務一旦開始不允許中斷。
2.2 基本模型
企業在決策前已知的信息包含:訂單規模,各訂單所需的生產時間與服務時間以及單位時間的提前、誤工與工期指派費用等。據此,定義參量如下:
n:訂單規模;


h[i]:訂單[i]的單位時間提前費用;
b[i]:訂單[i]的單位時間誤工費用;
a[i]:訂單[i]的單位時間工期指派費用;
企業直接決策的是訂單序列以及產品與服務的工期,間接決策的是訂單中產品與服務的完工時間。據此,定義決策變量如下:
seq:PSS訂單序列;
dp[i]:訂單[i]的產品工期,也是服務交付期的開始時間;
ds[i]:訂單[i]的服務交付期的截止時間;
ls[i]:訂單[i]的服務交付期長度,ls[i]=ds[i]-dp[i];
ctp[i]:訂單[i]的產品完工時間;
cts[i]:訂單[i]的服務完工時間;
其中,[i](i=1,2,…,n)表示訂單序列seq中第i個位置的訂單編號。此外,全文中令φ(·)和Φ(·)分別表示標準正態分布的概率密度函數和分布函數,并定義函數Ψ(x)=φ(x)-x[1-Φ(x)]。
根據問題描述和假設,給定任意PSS訂單序列seq,如果該序列的第一個訂單不在零時刻開始生產,或者在兩個相鄰的訂單之間插入空閑時間,或者在同一訂單的生產階段和服務階段之間插入空閑時間,都會推遲PSS的交付時間并產生更多工期指派費用,同時不會減少其它費用。因此問題的最優調度一定是非延遲調度,且第一個訂單一定在零時刻開始生產。基于以上分析,以最小化期望總費用為目標,建立優化模型如下:
minC(seq,dp,ls)=
(1)
(2)
cts[i]=max{ctp[i],dp[i]}+st[i],i=1,2,…,n
(3)
其中,dp=(dp[1],dp[2],…,dp[n])表示產品工期向量,ls=(ls[1],ls[2],…,ls[n])表示服務交付期長度向量。式表示目標為最小化產品的期望提前費用、產品與服務的期望誤工費用以及工期指派費用之和;式和分別定義了訂單[i]的產品和服務的完工時間。
3 問題求解
在現實中,服務型制造企業通常先通過調度訂單確定訂單序列,再根據訂單序列以及訂單的生產時間和服務時間等信息對訂單的完工時間進行估計,最后向客戶承諾一個合理的工期。如果先指派工期后確定序列,由于缺少訂單的排序信息,容易造成承諾的工期過短或過長。當工期過短時,由于生產時間和服務時間具有隨機性,容易發生誤工并產生誤工成本;而工期過長可能不被客戶接受甚至導致客戶流失,這時企業會被迫提供價格折扣來爭取訂單,由此產生工期指派成本。因此,為了更好地制定工期計劃和優化運營成本,企業需要先確定訂單序列再指派工期。但在學術研究中,通常采用逆序求解的方法,即先假設給定任意訂單序列,求得該序列下的最優工期,然后再返回決策最優訂單序列。這也是求解帶工期指派的調度問題常用的方法。
3.1 工期指派方法

C(seq,dp,ls)
(4)
式(4)仍然比較復雜,難以直接用于問題的分析和求解。為克服這一困難,本文提出一種可以得到近似最優解的方法,該方法的主要步驟如下:
步驟1:確定原目標函數的上界和下界,并用上下界的凸組合來近似原目標函數;
步驟 2:在給定任意訂單調度序列的條件下,計算近似目標函數的最優工期和最優值;
步驟3:基于近似目標函數的最優工期和最優值,設計啟發式算法尋找近似最優調度解。
按照上述方法,首先推導式(4)的近似值。記V[i]Φ(θ)[Φ(κ[i](θ))-1]dθ。由積分中值定理可知,存在ξ[i]∈(y[i],z[i])使得
V[i]=Φ(ξ[i])[Φ(κ[i](ξ[i]))-1](z[i]-y[i])
又由于0<Φ(ξ[i]),Φ(κ[i](ξ[i]))<1并且z[i]>y[i],因此有
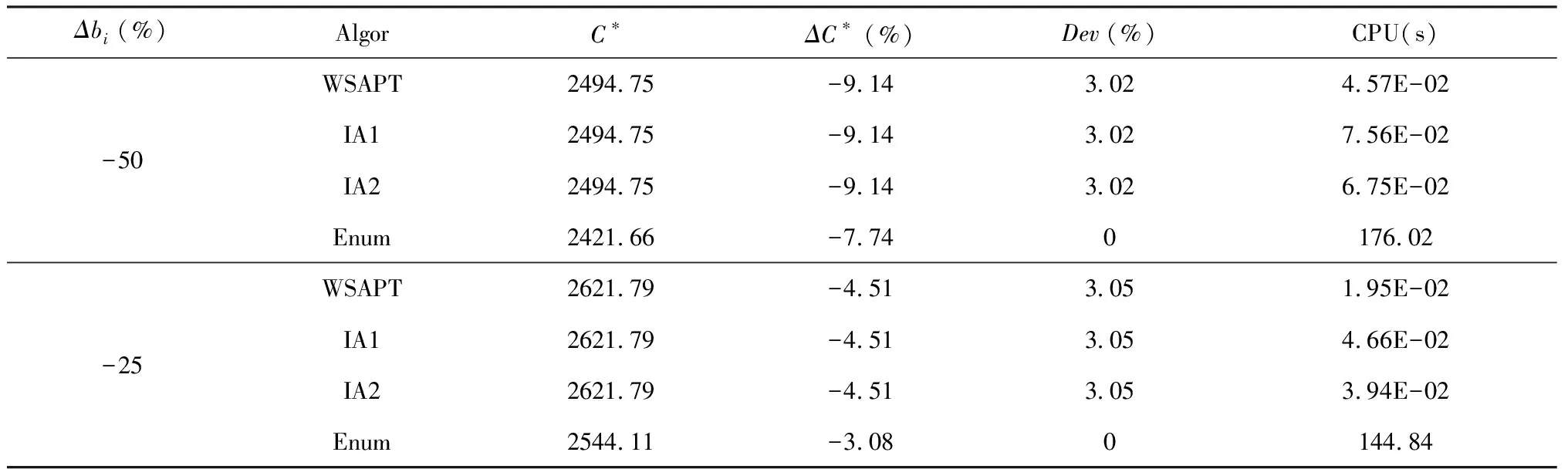
-(z[i]-y[i]) 由上式和式(4),C(seq,dp,ls)的近似值可表示為 (5) 其中τ[i]〗∈(0,1)。 定理1記 (6) (7) 聯立式(6)和式(7)可得 (8) 以及 (9) 定理2記 以及 δ[i] (10) (11) (12) 證明 對任意的i,j=1,2,…,n且i≠j,由式(6)和(7)得 λ1,[i] λ2,[i] 以及 (13) 其中, φ[i] 由上式和式(12)可得 其中η[k]a[k]+δ[k]/3。下面的定理給出了能夠最小化的近似最優排序規則。 定理3根據加權最短平均生產時間(weighted shortest average production time,WSAPT)排序規則: 可以得到問題 的近似最優調度解。 證明 令seq表示任意一個非WSAPT規則序列,則必存在兩個相鄰的訂單of和og(假設分別占據seq中[]和[+1]的位置)滿足 令seq′表示交換這兩個訂單位置得到新序列,有 以及 進而得到 上式表明交換訂單of和og的位置可以得到更優的序列。證畢。 根據定理3,利用WSAPT規則對原目標函數進行優化,可得到啟發式算法步驟如下: 算法WSAPT 步驟1:根據WSAPT排序規則輸出調度解seq*=([1],[2],…,[n]); 步驟2:根據式(13),求解約束優化問題 其中τ(ζ)=(τ[1](ζ),τ[2](ζ),…,τ[n](ζ)); 上述算法中,步驟1可利用快速排序實現,故計算復雜度為O(nlogn);步驟2和3的目的是為求解最優序列下原目標函數的最優工期和最優值,其中問題(14)的尋優速度由具體的優化算法所決定,一般可采用已有的且比較成熟的約束優化方法,如有效集(Active-set)算法和SQP(Sequential quadratic programming)算法等等。需要說明的是,要得到序列seq*下原目標函數的最優值,步驟2實際應當執行的操作是:根據式(4),求解如下的約束優化問題: (dp*,ls*)=argminC((dp,ls|seq*) s.t.dp[i],ls[i]>0,i=1,2,…,n (15) 然而,該問題中含有2n個決策變量,當訂單規模稍大時(如n≥7),問題(15)會非常耗費時間。因此,考慮在算法WSAPT中以犧牲一定的求解精度為代價,將2n維優化問題降為一維優化問題以換取時間效率。 由于WSAPT規則是基于近似目標函數上界得到的調度規則,通過WSAPT算法得到的調度解可能會與原目標函數的最優調度解存在較大偏離,因此需要引入優化機制進一步提高解的質量。本文的改進方法為:首先利用WSAPT規則產生初始解,然后對該初始解執行插入鄰域局部搜索,最后選取目標值最小的解作為新的初始解。據此,提出改進的啟發式算法如下: 算法IA1(inserting algorithm 1) 步驟1:根據WSAPT排序規則生成初始調度解seq0=([1],[2],…,[n]); 步驟2:令j=1并構建部分序列seqp=([j]),其中[j]是seq0中第j個位置的訂單; 步驟3:將訂單[j+1]插入到seqp的第k個位置,同時將該位置及后面的訂單順序后移一位,從而形成新序列seqk,其中k=1,2,…,j+1。根據式(13),計算 (16) 步驟4:令j=j+1。如果j=n,輸出seq*并轉步驟5;否則令seqp=seq*,轉步驟3; 步驟5:根據式(13),求解約束優化問題; 算法IA1的計算復雜度為O(n3)。考慮到當訂單規模較大時,算法IA1中步驟3會非常耗費時間。為了解決這一問題,可以在該步驟中對k設置一個自適應下界,使其無需試探seqp中所有可能的插入位置,就能達到與遍歷所有位置相同或相近的優化效果,同時能夠節省大量的運行時間。記j(n)max(1,j-「n/10?),其中「x?表示不小于x的最小整數。基于算法IA1,提出改進算法如下: 算法IA2(inserting algorithm 2) 步驟0-2,4-6與算法IA1相同,步驟3變為: 步驟3:將訂單[j+1]插入到seqp的第k個位置,將該位置及后面的訂單順序后移一位,從而構成新序列seqk,其中k=j(n),j(n)+1,…,j+1。根據式(13),計算式(16)。 首先,考察三種算法的優化效果對初始化參數τi(ζ0)的敏感性。通過大量實驗發現,訂單規模不會對本實驗的結論產生實質性的影響,因此本文僅展示四種訂單規模n={10,20,30,40}的測試結果,每種訂單規模包含20個隨機算例。由于ζ0∈(0,1),故考慮測試ζ0={0.1,0.3,0.5,0.7,0.9}。對于每種訂單規模,統計各算法在不同ζ0取值下求解20個算例的平均目標值,結果如圖2所示。在圖2中,算法IA1和IA2的曲線接近于重合,這是由于兩種算法的優化效果十分相近。 由圖2可見,各算法關于參數ζ0的單調性均是不確定的,但是各算法所得目標值的波動幅度均小于5‰,因此ζ0對三種算法優化效果的影響都很小,說明這些算法對τi初始值的擾動均具有較強的魯棒性。正是由于這種魯棒性,使得各算法在對ζ進行重新尋優后,無需再基于最優值ζ*調整已得到的最優訂單序列。對于WSAPT算法,圖2(A)表明當n=10時,ζ0的不同取值并未對算法性能產生影響;由圖2(B)和2(C)可見,當n=20或n=30時,ζ0取值大于0.5會使算法性能下降;圖2(D)則表明當n=40時,ζ0取值為0.3要優于其它取值。綜合來看,對于WSAPT算法,ζ0的一個合適取值是0.3。對IA1和IA2算法的結果進行類似分析,可將兩種算法中ζ0的值選定為0.7。 下面考察各算法的優化結果對單位時間提前費用、誤工費用和工期指派費用的敏感性。通過大量實驗發現,敏感性分析的實驗結論適用于任意規模的算例。因此,這里僅展示一個隨機產生的小規模(n=5)測試問題的相關結果,該問題的參數由表1給出。 圖2 參數ζ0對各算法所得目標值的影響 針對該測試問題,分別應用各算法對單位時間的提前費用hi、誤工費用bi和工期指派費用ai進行敏感性分析,得到各算法的優化結果如表2-4所示。其中,Δhi、Δbi和Δai分別表示hi、bi和ai的變動百分比;C*表示目標值;ΔC*表示目標值的變動百分比;Dev是衡量算法求解質量的指標,表示與已知最好解的相對偏離率,其計算公式可表示為 其中,Algor表示當前算法名稱,C*(Algor)表示當前算法得到的目標值,Cbest表示所有參與比較的算法所獲得的最好目標值;CPU表示計算時間;Enum表示基于枚舉方法的精確求解算法,通過該算法一般可以得到問題的最優解。 表1 訂單規模n=5的測試問題參數 表2 hi的敏感性分析及算法比較結果 續表2 hi的敏感性分析及算法比較結果 由表2可見,當提前費用hi在-50%~50%變化時,對于Enum算法,總費用C*的變動范圍僅為-2.80%~2.07%;而對于本文所提的三種算法,總費用C*的變動范圍也僅為-2.25%~1.69%。這說明了通過三種算法獲得的PSS訂單調度優化策略較少受到庫存費用偏差的影響。在企業的實際運營中,通常很難精確估計庫存費用,然而在此算例下提前費用偏差對總費用的影響很小,因此決策者即便難以準確估計庫存費用也能采用本文算法制定出比較有效的PSS訂單調度策略。 由表3可見,當誤工費用bi在-50%~50%變化時,對于Enum算法,總費用C*的變動范圍為-7.74%~4.24%;對于本文所提的三種算法,總費用C*的變動范圍為-9.14%~9.29%。只有當總費用的構成中有比較少的延遲相關費用時,總費用才不會因誤工費用的變化而產生較大波動。因此,本文提出的PSS訂單調度策略能夠比較有效地減少訂單誤工的發生。 由表4可見,工期指派費用ai在-50%~50%變化時,對于Enum算法,總費用C*的變動范圍為-43.16%~41.62%;對于本文所提的三種算法,總費用C*的變動范圍為-39.01%~39.49%。因此,工期指派費用偏差對于PSS訂單調度費用的影響很大,決策者在估計工期指派費用時需要格外謹慎。 表3 bi的敏感性分析及算法比較結果 續表3 bi的敏感性分析及算法比較結果 表4 ai的敏感性分析及算法比較結果 此外,表2~4還對各算法求解問題的有效性進行了初步對比,可以看出: (1)WSAPT、IA1和IA2的求解速度比精確算法Enum快4個數量級,因此時間效率優勢十分明顯; (2)隨著誤工費用的增加或工期指派費用的減少,本文算法的求解質量出現了較為明顯的下降,這主要是因為當誤工費用與工期指派費用間的差值變大時,近似費用函數與原費用函數的偏差會逐漸加大,從而使算法的優化效果變差;其次,本文算法采用降維尋優策略也會使求解質量有所下降。 最后用一組隨機產生的算例來測試本文算法的有效性。選取訂單規模n={20,40,60,80,100},對于每種訂單規模隨機產生50個算例,從而可以得到5×50=250個算例所組成測試算例集。 對于該組問題,衡量各算法求解質量的指標為與已知最好解的相對偏離率Dev(Algor)和獲得最好解的概率Pgb(Algor),后者的計算公式為: Pgb(Algor)= 由表5可得如下結論: (1)算法IA1和IA2的相對偏離率和獲得相對最好解的概率均明顯優于WSAPT,因此基于WSAPT規則生成初始序列,再進一步利用插入鄰域局部搜索進行優化的思路是正確且有效的; 表5 不同問題規模下的實驗結果 (2)IA2的求解質量非常接近IA1,同時IA2的運行時間更短,并且問題規模越大其時間效率優勢越明顯,故IA2的改進策略是有效的; (3)隨著訂單規模逐漸增大,IA1的兩個求解質量指標并未顯著變化,而IA2獲得最好解的概率在逐漸下降,因此IA1的求解質量更穩定; (4)綜合來看,當問題規模較小時,為了保證求解質量應當采用IA1算法,而當問題規模較大時適宜采用IA2算法,因為它能夠兼具較高的求解質量與時間效率。 訂單調度一直是企業運營管理的研究熱點和難點之一,而目前對PSS訂單調度問題的研究尚處于起步階段。本文針對由一個制造工廠和多個區域服務中心組成的服務型制造企業,考慮生產與服務時間均具有隨機性,構建了PSS訂單調度與工期指派聯合決策問題的數學模型,并設計了啟發式算法對問題進行求解。通過數值仿真的分析結果可以看出,本文的模型與算法可以在較短的時間內得到較高質量的解,同時對決策過程中相關調度參數的不確定性具有一定的魯棒性,因此能夠幫助服務型制造企業的調度人員做出合理、高效的PSS訂單調度安排,同時對于服務型制造企業降低運營成本和提高服務質量也具有一定的參考價值。未來的研究方向可考慮如何設計高效的智能仿生算法來求解本文提出的問題。 附錄A 由公式推出公式的詳細過程: E[max{dp[i]-ctp[i],0}]= (A1) 其中 (A2) 同理,訂單[i]的產品的期望延誤可化簡為: (A3) 令r[i](t)=ds[i]-max{t,dp[i]}以及g[i](s,t)=fst[i](s)fctp[i](t),其中 (A4) (A5) 類似式(A2)和(A3)的推導過程,通過積分運算易得: (A6) (A7) 以及 (A8) 下面對式(A7)進行變換。根據鏈式法則,有 (A9) 應用分步積分法,由式(A9)可得: (A10) 將式(A6)-(A8)和(A10)代入式(A5),得: (A11)
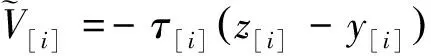

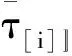
















3.2 啟發式算法設計

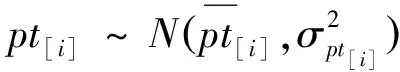










4 數值實驗









5 結語






