基于組合模型的云南省卷煙需求預測與結果評價研究

趙旻，張丹楓，曾中良，謝東風，李青，徐路寧

1 云南省煙草專賣局（公司），信息中心，云南省昆明 650000；

2 云南省煙草專賣局（公司），卷煙銷售管理處，云南省昆明 650000；

3 北京中軟國際信息技術有限公司，互聯網ITS集團MSO中心，北京海淀 100000

目前關于卷煙需求預測的研究成果有很多。文獻[1]利用1997-2002年中國煙草行業和相關經濟學指標，從宏觀層面構建了我國卷煙消費需求的數學模型，認為居民消費支出、卷煙價格、地區差異、經濟增長、產業升級、城鄉居民消費差異和卷煙平均消費傾向等因素對我國卷煙需求具有顯著影響。文獻[2]以2008-2012年云南省宏觀經濟數據和銷售數據為基礎，通過脈沖響應函數得到宏觀經濟對卷煙市場運行的影響具有一定的滯后效應；方差分解分析結果顯示在短期和中期投資對卷煙市場拉動的效果最為顯著，消費對卷煙市場拉動的效果最不顯著。文獻[3]基于2007-2013云南省宏觀經濟數據和銷售數據，分析城鎮農村市場差異，明確了對農村城鎮市場分別進行預測分析的思路，提出了銷售額數據按照不同CPI還原的思路，降低數據受價格指數變動影響程度；并運用PCA主成分分析，對銷售數據基于宏觀經濟數據的表達式進行了解讀。但現有的卷煙需求預測研究存在一些不足，首先，都是運用當期的宏觀經濟指標預測當期的卷煙銷量，實際可操作性較差，不能滿足煙草行業的預測需求；其次，文獻中均未基于預測實際情況，開展模型的穩定性評價研究。

本文構建了一種適合云南煙草行業需求預測的方法體系，并對需求預測模型進行了動態評判。

1 需求預測思路

由于各品類季節性差異大，銷售曲線完全不同，可以按品類單獨構建預測模型來預測其銷量。

本文運用IBM SPSS Modeler為分析工具，以云南省2009-2016年的宏觀經濟數據和卷煙銷量數據為基礎，構建組合預測模型預測云南省卷煙銷量。在數據處理階段，運用居民消費價格指數（CPI）對宏觀數據和銷量數據進行處理[3]；在指標選擇上，運用時差相關分析法和簡單相關分析法分析宏觀經濟指標與卷煙銷量的相關關系，選擇了科學的模型指標，在預測時間點運用宏觀經濟數據進行回歸；在模型構建上，通過構建組合預測模型[4][5][6]（ARIMA模型[7]和回歸模型[8]）預測卷煙銷量；在對模型穩定性評價上，通過計算模型的預測精度、置信度等對模型進行實時評價，構建了新的評價體系，確保預測模型科學可信。

2 預測過程

以對云南省卷煙總量預測為例，對宏觀經濟指標選擇、模型構建、模型評價等過程進行分析及說明。

2.1 數據獲取及預處理

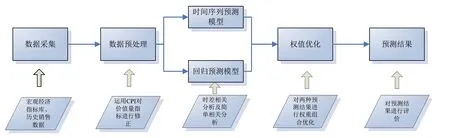
圖1 需求預測路徑Fig.1 The route of demand forecast

宏觀經濟領域的經濟活動會在一定程度上影響和反映卷煙需求市場波動狀況。通過查閱文獻資料，結合數據可得性，選定規模以上工業增加值、固定資產投資、社會消費品零售總額、進出口貿易總額、地區生產總值、第一產業增加值、第二產業增加值、第三產業增加值、農林牧漁服務業總產值、城鎮常住居民人均可支配收入、城鎮居民人均消費支出、農村居民人均現金收入、居民消費價格指數（CPI）、第三產業占GDP比值等指標進入備選指標庫。

考慮到宏觀數據的情況，采用季度數據進行預測，2009年1季度到2016年3季度共31個樣本。CPI反映居民家庭購買消費商品及服務價格水平的變動情況。本文利用居民消費價格指數（CPI）對本研究中涉及貨幣的數據進行價格可比調整，逐期縮減至基期，折算CPI原始值。現有CPI數據共有城鎮CPI、農村CPI、綜合CPI、煙酒食品CPI等若干細分類。本文選擇2010年1月為基期，所有月份CPI均先逐年同比到2010年同月，再環比折回2010年1月。

2.1.1 原始的CPI計算原理

現將原始CPI同除以100，即得到：

2.1.2 將所有的CPI1換算成2010年對應月份為基期的同比CPI2。

如：求2008年9月同比2010年9月的CPI1，即：

2.1.3 以2010年對應月份為基期的同比CPI2，換算成以2010年1月為基期的CPI3。

如：求CPI3（2007.3/2010.1）

2.1.4 2010年各月環比的求解

由：環比的增長率=當期消費價格/上一期消費價格-1

則有：環比CPI=1+環比增長率

已知CPI綜合2012年各月的環比，及2012年對應2011年各月同比消費價格指數，求2011年各月環比，配合2011年對應2010年各月同比CPI，進而求得2010年各月的環比 CPI。

2.1.5 對應分析周期處理數據周期

CPI綜合用于GDP、社會零售品總額、固定資產投資經濟指標換算，CPI煙酒用于銷售額換算。各類型的CPI算法相同，均為折算到同一個基期。

2.2 指標體系構建

2.2.1 指標選擇方法

本文運用時差相關分析和相關分析法來對指標進行篩選，再將與卷煙銷量有較強相關關系的宏觀經濟指標納入回歸模型對卷煙需求進行預測，同時考慮到宏觀經濟指標公布的滯后性以及經濟指標本身反映經濟活動的滯后性，引入滯后期概念，運用先行宏觀經濟數據預測當期銷量。

● 時差相關分析

時差相關分析是利用時差相關系數驗證經濟時間序列先行、一致、滯后關系的一種常用方法。選定應變基準指標，使被選自變指標超前或滯后基準指標若干期，計算它們的相關系數，最大的相關系數對應的移動月數為該應變指標延遲數。即：設基準指標為Y，被選指標為X，然后計算Y和X的時滯為k的時間序列之間的相關系數kr（k=0，±1，±2，…），能使相關系數最大的時滯k，即為該指標的先行或滯后月份。

式中k表示超前或滯后期，k取負值時表示超前，取正數時表示滯后，k被稱為時差或延遲數。一般來講，最大的時差相關系數最好大于0.5，這樣說明時滯性比較明顯，否則說明入選的指標的時滯意義不明顯。

● 相關分析

相關分析是變量之間相關程度的指標。相關系數的取值在-1到1之間。

2.2.2 指標篩選結果

以卷煙銷量為基準指標，以宏觀經濟指標為備選指標進行時差相關分析。通過時差相關分析結果發現規模以上工業增加值、進出口貿易總額、農村居民人均現金收入和第三產業占GDP比重4個指標先行1-4期與卷煙銷量的相關系數都小于0.5，說明這六個指標與卷煙銷量的相關性較低，對預測卷煙銷量的貢獻較小，從備選指標庫刪除。

表1 時差相關分析結果Tab.1 The result of time difference correlation analysis

再通過宏觀經濟指標間的相關性分析，將高度相關的幾個指標用一個指標來替代，用此指標反映這一類指標對卷煙銷量的影響，即通過主成分分析，避免較多指標的搜集工作，提高工作效率。

下表是地區生產總值與其他宏觀經濟指標間的相關系數，地區生產總值與第一產業總值、第二產業總值、第三產業總值的相關系數均高于0.9，且這四個指標均反映生產總值數據，反映的經濟因素相似，故用地區生產總值替代這一類指標。從備選指標庫刪除第一產業總值、第二產業總值、第三產業總值。

表2 第一產業總值與其他各宏觀經濟指標相關系數表Tab.2 The correlation coefficient between total production value of the primary industry and other macroeconomic indicators

綜上，云南卷煙銷量預測的宏觀經濟指標池保留固定資產投資、社會消費品零售總額、地區生產總值、農林牧漁服務業總產值、城鎮常住居民人均可支配收入、城鎮居民人均消費支出、期末常住人口。

2.3 預測模型構建

2.3.1 預測模型方法[5][6][7][8][9][10]

運用篩選后的宏觀經濟指標和卷煙銷量分別建立回歸預測模型和時間序列預測模型對不同品類的卷煙市場需求進行預測，再進行預測結果擬合。

● 時間序列模型

ARIMA模型[7]是現代時間序列預測的一種常用方法（又叫博克思-詹金斯法），即求和自回歸移動平均模型，預測模型為：

其中q為滑動平均模型的階數，Yt為時間序列在t期的觀測值，et是時間序列模型在期的誤差或偏差，et-q是時間序列模型在t -q期的誤差或偏差，φ1,φ2,...,φp是滑動平均模型的參數。

● 回歸預測模型

本文主要運用多元線性回歸[8]進行市場預測,了解兩個或多個變量間是否相關、相關方向與強度，并通過處理多變量間相關關系形成一個統計預測模型以觀察特定變量預測銷量銷售額數據。

● 最小二乘法確定組合預測模型權重[9]

得到時間序列及回歸預測模型預測結果后，構造二次規劃的模型，其

約束條件為

其中i為預測模型的種類，k為用來預測的模型的總數，Yt為實際值（或觀測值），為預測值，構造式的廣義拉格朗日函數在極值點應滿足，分別對ω、λ求偏導得方程組，通過解這個的方程組，即可以得到各權重系數ωi。

運用矩陣計算簡化模型計算。設在某個時刻t的觀察值（實際值）為Yt，設第i種預測方法的組合系數或權重為ωi，取權向量，且滿足

于是組合預測模型寫成向量形式為

我們運用k種預測方法，對n個數值進行預測得到n×k矩陣的預測矩陣為

則上式可寫為 AW = Y

運用矩陣的運算ATAW=ATY

則運用矩陣的計算可以求出權向量W。

2.3.2 預測模型及結果

運用云南省2009年1季度至2016年3季度的宏觀經濟數據和卷煙銷量數據，通過構建組合預測模型，預測云南省2016年4季度及2017年1季度的卷煙總需求量。

對卷煙銷量的歷史數據進行時間序列預測，記一階差分調整后的銷量序列為，建立ARIMA（1,1,1）模型：

模型調整后的R2為0.89，擬合度較高。

本文運用先行兩期的宏觀經濟指標數據對當期卷煙需求進行預測，運用逐步回歸法最終進入回歸模型的指標有國內生產總值（GDP）、社會消費品零售總額（consume）、城鎮居民人均可支配收入（income）三個指標，記回歸預測值為，建立回歸模型：

模型調整后的R2為0.93，擬合效果較好。

運用最小二乘法計算兩個預測模型的權重，運用最小二乘法計算兩個預測模型的權重，根據前面的定義可知

得

從而：

最終得到2016年4季度及2017年1季度的預測結果如下表所示，從表中可知，跟實際銷量相比預測結果的誤差均在3%以下，預測結果可信。

表3 云南省總量預測結果Tab.3 The forecast result of Yunnan cigarette demand

圖2 云南省一類煙銷量預測擬合效果Fig.2 Fitting result of thefirst class cigarette sales forecast of Yunnan

同理，分別構建云南省一類煙、二類煙、三類煙的預測模型，得到各品類卷煙的擬合效果如下三圖所示：

圖3 云南省二類煙銷量預測擬合效果Fig.3 Fitting result of the second class cigarette sales forecast of Yunnan

圖4 云南省三類煙銷量預測擬合效果Fig.4 Fitting result of the third class cigarette sales forecast of Yunnan

2.4 模型評價

2.4.1 模型評價方法

通過查找相關文獻[11]發現，對模型穩定性評價研究較少。本文創新性的以歷史建模預測誤差為基礎，計算不同誤差值的置信度，根據可接受的置信度范圍對模型穩定性進行判定，確保模型科學可靠。

評價標準及計算步驟如下：

1.根據業務需要設定預測精準度及預測精準度置信度，本文設定預測精準度=90%，置信度=88%

2.計算預測模型的預測精準度。

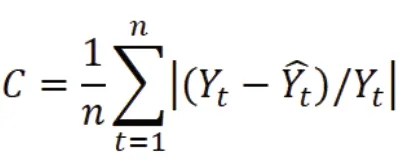
3.計算預測精準度的置信度。

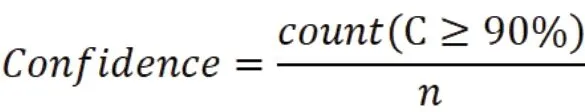
4.根據設定的預測精準度和置信度對模型穩定性進行評價，若模型未達到設定標準，則重新建模進行預測。

2.4.2 模型評估結果

2010年1季度至2016年3季度云南省預測模型的擬合誤差如下圖，組合預測模型的預測誤差波動相對比較穩定，雖然不能保證每個時點的預測精度最低，但用組合模型對所有時點的預測是最優的，預測結果也更加貼近實際結果。基于組合預測模型的預測誤差，計算其不同預測精準度下的置信度。鑒于不同地區的銷量變化趨勢不同，構建的預測模型不同，需針對不同的情況設定不同的評價標準。

本文確定三類評價標準：

A級：模型預測精準度90%以上，置信度90%以上，共有4個地市（含云南省）滿足；

圖5 云南省總量預測模型誤差比較圖Fig.5 Comparison diagram of prediction error among three methods

B級：不滿足A級標準，但模型預測精準度85%以上，置信度88%以上，共有12個地市滿足；

C級：不滿足A、B級標準，模型預測精準度85%以上，置信度88%以下，共有1個。

云南省總量預測模型預測精準度為90%時，置信度92.85%；預測精準度85%時，置信度100%。根據設定的評判標準，則可將云南省總量預測模型評為A級，此預測模型穩定性較好，預測結果科學可信。

針對A級預測結果的地市，預測結果可直接運用，針對B級預測結果的地州，進行進一步的觀測與數據追蹤，針對C級預測結果地州，需逐個具體進行分析，對基礎數據、業務開展情況、模型科學性進行進一步驗證。

3 結論

本文以云南省宏觀經濟數據和銷量數據為基礎，構建了一套合理的適合煙草行業需求預測的方法，并通過實際驗證得到云南需求預測結果誤差在3%以內，模型穩定性評價為A級。本文的創新之處有以下幾點：一是鑒于宏觀經濟數據公布的滯后性，并考慮到卷煙行業需求預測的實際需求，在驗證可行的情況下，在模型構建階段，運用先行兩期的宏觀經濟指標來預測當期的卷煙需求量，預測結果科學有效。二是在組合預測模型的權重計算上，運用最小二乘法計算回歸預測模型和時間序列預測模型的權重，確保組合預測模型結果的科學性。三是在對模型穩定性評價上，以建模預測結果的平均相對誤差及置信度為基礎，研究出了一套適合云南卷煙需求預測的模型評判標準，并運用判定標準對模型的穩定性進行判定，確保模型科學可靠。