基于時間-空間譜配法的分?jǐn)?shù)階微分方程的一種解法

王龍,趙丹

?

基于時間-空間譜配法的分?jǐn)?shù)階微分方程的一種解法

王龍,趙丹

四川職業(yè)技術(shù)學(xué)院, 四川 遂寧 629000

隨著分?jǐn)?shù)階微分方程的應(yīng)用領(lǐng)域越來越廣泛，相應(yīng)的理論研究也變得更加重要。本文針對時間分?jǐn)?shù)階的經(jīng)典微分方程，提出一種加入空間譜配的解法。通過對時間分?jǐn)?shù)階經(jīng)典微分方程的推導(dǎo)，得出等價的微分方程并獲取空間配置點(diǎn)，然后應(yīng)用高斯積分公式轉(zhuǎn)變空間，求出轉(zhuǎn)換方程的積分項(xiàng)。數(shù)值驗(yàn)算結(jié)果表明：采用時間-空間譜配法得出的精確解與數(shù)值解吻合程度較好，基本能滿足分?jǐn)?shù)階微分方程高精度近似解的要求。

分?jǐn)?shù)階微分方程; 時間-空間譜配法; 精確解; 數(shù)值解

分?jǐn)?shù)階微分方程已經(jīng)有300多年歷史，但一直以來關(guān)于它的研究只停留在純數(shù)學(xué)領(lǐng)域。近三十年以來，分?jǐn)?shù)階微分方程開始被廣泛應(yīng)用于光學(xué)、生物學(xué)、熱學(xué)、流變學(xué)、金融學(xué)和物理學(xué)等領(lǐng)域，受到了人們的關(guān)注。關(guān)于分?jǐn)?shù)階微分方程的精確解求得非常不容易，在實(shí)際應(yīng)用中一般只需要精度較高的近似解即可，因此高精度近似解的求得具有較大的實(shí)用價值。Amele等人提出了分?jǐn)?shù)階微分方程的一種擴(kuò)散形式，主要是在時空方向上形成一階差分，但需要具備穩(wěn)定條件[1]。Temirkhan等人對基于時間分?jǐn)?shù)階的擴(kuò)散方程進(jìn)行求解，該方法收斂性的推導(dǎo)主要基于先驗(yàn)誤差的估算[2]。Ghomanjani通過有限元對時間與空間分?jǐn)?shù)階的微分方程進(jìn)行求解[3]。Mohammed等人使用有限差分法對時間分?jǐn)?shù)階微分方程進(jìn)行求解，然后給出了方程誤差的估計(jì)[4]。本文在時間分?jǐn)?shù)階經(jīng)典微分方程的基礎(chǔ)上加入了空間譜配，通過時間-空間譜配法研究了分?jǐn)?shù)階微分方程的一種解法。

1 時間分?jǐn)?shù)階的經(jīng)典微分方程

在上式中，(,)代表粒子的概率密度函數(shù)，該粒子的位置是，時間是。代表粒子質(zhì)量。1代表粒子與環(huán)境的摩擦系數(shù)。1為擴(kuò)散函數(shù)。

時間分?jǐn)?shù)階外場存在反常擴(kuò)散，為了描述該情景，需要考慮用以下的時間分?jǐn)?shù)階微分方程：

滿足以上方程的初始條件：(,0)=()，<<。滿足以上方程的邊界條件：(,)=1()，(,)=2()，0<<。

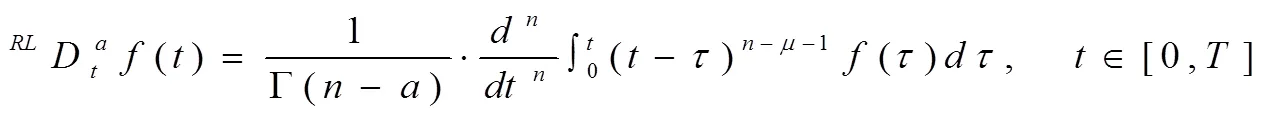
在上式中，代表正整數(shù)，而且0≤-1<≤。

2 基于時間-空間譜配法的分?jǐn)?shù)階微分方程求解過程

2.1 求解過程

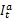
在上式中，代表正整數(shù)，且0≤-1<≤。

由于IμtDμtZ()=()-(0)，上式也可以用以下方程表示：

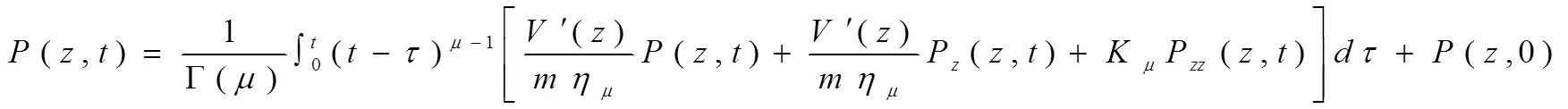
(,)相應(yīng)初始條件：(,0)=()，<<；邊界條件：(,)=1()，(,)=2()，0<<。為了使正交多項(xiàng)式，進(jìn)行以下變量轉(zhuǎn)換：

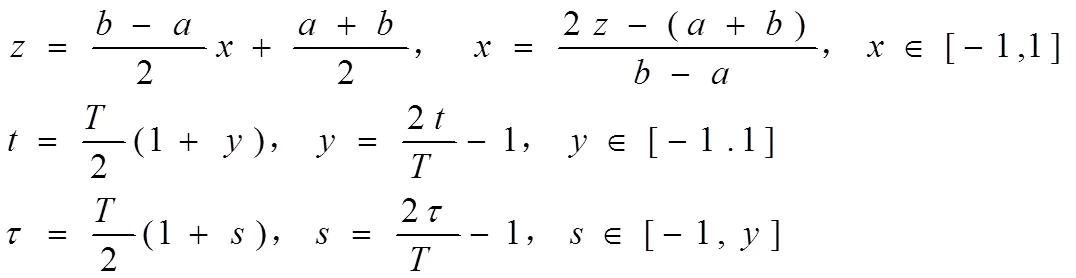
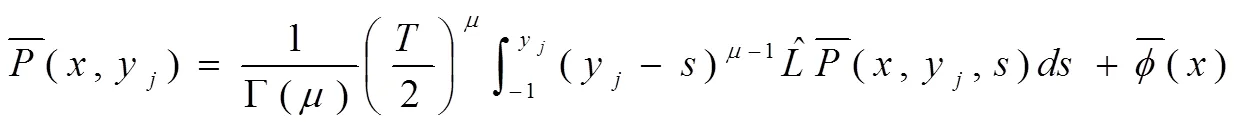
為更好地應(yīng)用高斯積分公式，需要作出空間的線性改變，從空間[-1,y]轉(zhuǎn)變到空間[-1,1]：

最后配置空間，在[-1,1]中獲取配置點(diǎn){x}，使式（12）在配置點(diǎn)成立，得出下式：

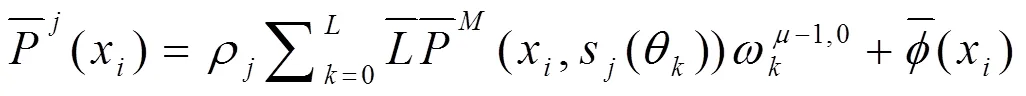
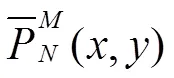
2.2 數(shù)值驗(yàn)算

為驗(yàn)證本文提出的基于時間-空間譜配法的分?jǐn)?shù)階微分方程求解有效性，采用以下算例。

例1：計(jì)算分?jǐn)?shù)階微分方程數(shù)值解與精確解的吻合情況。設(shè)方程如下：

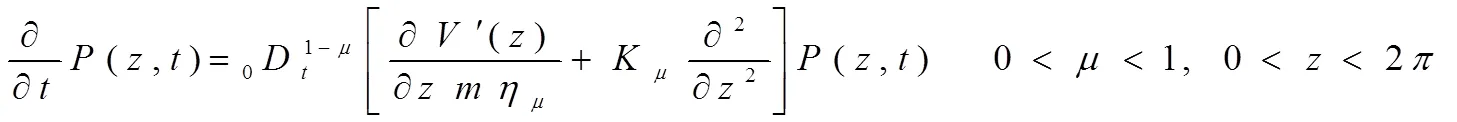
當(dāng)例1中的=0.9，精確解與數(shù)值解情況如圖1所示。當(dāng)=0.8，=1或者=0.9202，精確解與數(shù)值解比較如圖2所示。根據(jù)以上數(shù)值驗(yàn)算，采用時間-空間譜配法得出的精確解與數(shù)值解吻合程度較好，基本能滿足分?jǐn)?shù)階微分方程高精度近似解的要求。

圖 1=0.9時的精確解與數(shù)值解

Fig.1 Exact and numerical solutions for=0.9

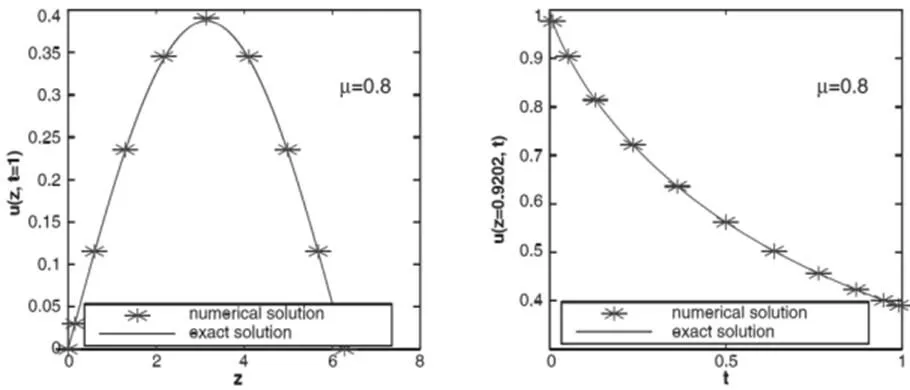
圖 2 左圖=1、右圖z=0.9202，精確解與數(shù)值解的比較

3 討論

隨著分?jǐn)?shù)階微分方程的使用領(lǐng)域日益擴(kuò)大，關(guān)于方程解的研究也越來越多，大多數(shù)研究都是圍繞方程解的唯一性和存在性而展開的。對于線性分?jǐn)?shù)階微分方程的求解，Hamani等提出要借助特殊函數(shù)工具進(jìn)行方程解的探索[5]。對于非線性分?jǐn)?shù)階微分方程的求解，Doan等認(rèn)為需要將原方程轉(zhuǎn)化為等價的微積分方程，在適當(dāng)空間中使用不動點(diǎn)定理[6]。Hassan等圍繞時間分?jǐn)?shù)階的微積分方程求解過程，認(rèn)為要適當(dāng)考慮函數(shù)空間的問題，這有利于提高數(shù)值解的精確性[7]。相對來說，分?jǐn)?shù)階微分方程的理論研究滯后于實(shí)踐應(yīng)用，但隨著學(xué)者們的廣泛重視，在理論研究方面將會有較大的進(jìn)展。

4 結(jié)論

針對分?jǐn)?shù)階微分方程高精度近似解求得問題，提出一種基于時間-空間譜配法的解法，使時間分?jǐn)?shù)階的經(jīng)典微分方程能夠在空間方向的配置點(diǎn)成立，形成全離散格式，但要滿足配置點(diǎn)的要求。通過數(shù)值驗(yàn)算，求得的數(shù)值解較好地接近精確解。本文解法的優(yōu)勢在于能夠通過較少的配置點(diǎn)得出精度較高的數(shù)值解，在節(jié)省儲存空間的同時，還能求解較為復(fù)雜的分?jǐn)?shù)階微分方程。

[1] Taieb A, Dahmani Z. A new problem of singular fractional differential equations[J]. Journal of Dynamical Systems and Geometric Theories, 2016,14(2):165-187

[2] Aleroev T, Kekharsaeva E. Boundary value problems for differential equations with fractional derivatives[J]. Integral Transforms and Special Functions, 2017,28(12):900-908

[3] Ghomanjani F. A new approach for solving fractional differential-algebraic equations[J]. Journal of Taibah University for Science, 2017,11(6):1158-1164

[4] ALHorani M, Khalil R. Total fractional differentials with applications to exact fractional differential equations[J]. International Journal of Computer Mathematics, 2018,95(6):1444-1452

[5] Hamani S, Hammou A, Henderson J. Impulsive fractional differential equations involving the hadamard fractional derivative[J]. Communications on applied nonlinear analysis, 2017,24(3):48-58

[6] Doan TS, Huong PT, Kloeden PE,. Asymptotic separation between solutions of Caputo fractional stochastic differential equations[J]. Stochastic Analysis and Applications, 2018,36(4):654-664

[7] Hassan K, Muhammad AS, Tauseef MD,Numerical solutions to systems of fractional Fredholm Integro differential equations, using Chebyshev wavelet method[J]. Journal of Taibah University for Science, 2018,12(5):584-591

A Solution of Fractional Differential Equations on Time-space Spectrum Allocation Method

WANG Long, ZHAO Dan

629000,

With the application of fractional differential equation more and more widely, the corresponding theoretical research has become more important. In this paper, we propose a solution to the classical differential equation of fractional order in time by adding spatial spectral assignment. By deducing the classical differential equation of time fractional order, the equivalent differential equation is obtained and the spatial collocation points are obtained. Then the integral terms of the transformation equation are obtained by applying the Gauss integral formula to transform the space. The numerical results show that the exact solution obtained by the time-space spectrum matching method is in good agreement with the numerical solution, and can basically meet the requirements of high-precision approximate solution of fractional differential equation.

Fractional differential equations; Time-space spectrum allocation method; exact solutions; numerical solutions

O29

A

1000-2324(2019)01-0142-03

10.3969/j.issn.1000-2324.2019.01.032

2018-02-10

2018-04-20

四川省教育廳一般基金項(xiàng)目:偏微分方程圖像分割算法研究(15ZB0358)

王龍(1983-),男,碩士,副教授,主要研究方向?yàn)槠⒎址匠蹋瑪?shù)學(xué)建模，應(yīng)用數(shù)學(xué). E-mail:wanglongzhujun@163.com