小樣本數(shù)據(jù)的MIFS過(guò)濾式特征選擇算法

王波,李時(shí)輝,鄭鵬飛

?

小樣本數(shù)據(jù)的MIFS過(guò)濾式特征選擇算法

王波,李時(shí)輝,鄭鵬飛

義烏工商職業(yè)技術(shù)學(xué)院, 浙江 義烏 322000

針對(duì)小樣本數(shù)據(jù)特征選擇以及最佳特征難確定的問(wèn)題，本文提出一種MIFS過(guò)濾式特征選擇算法，同時(shí)結(jié)合Boruta算法，旨在降低數(shù)據(jù)集維度，確定出最佳特征的子集。通過(guò)實(shí)驗(yàn)結(jié)果與分析，對(duì)比其它三種傳統(tǒng)的過(guò)濾式算法，驗(yàn)證本文算法的有效性。結(jié)果表明：MIFS-Boruta算法體現(xiàn)出更廣的特征選擇量，并且平均最低分類(lèi)錯(cuò)誤率最低。

小樣本; MIFS; 算法

隨著互聯(lián)網(wǎng)及信息技術(shù)的發(fā)展，大數(shù)據(jù)應(yīng)用越來(lái)越普遍，但在實(shí)際生活中，小樣本數(shù)據(jù)依然不可或缺。例如基因分析數(shù)據(jù)就是一種典型的小樣本數(shù)據(jù)，主要由微陣列實(shí)驗(yàn)進(jìn)行獲取，而實(shí)驗(yàn)成本一般比較昂貴，這對(duì)實(shí)驗(yàn)次數(shù)產(chǎn)生了限制。整個(gè)基因分析數(shù)據(jù)規(guī)模較小，但數(shù)據(jù)維數(shù)很高，若采用傳統(tǒng)型的機(jī)器學(xué)習(xí)算法進(jìn)行處理，容易導(dǎo)致數(shù)據(jù)失效。而利用特征選擇降低數(shù)據(jù)的維數(shù)，則是一種較為有效的解決辦法。特征選擇有利于去除數(shù)據(jù)的不相關(guān)性和冗余性，提升數(shù)據(jù)本身的質(zhì)量，減少數(shù)據(jù)集計(jì)算的代價(jià)，進(jìn)而使數(shù)據(jù)挖掘變得更快[1]。常用的特征選擇方法有過(guò)濾法、封裝法和嵌入法[2]。過(guò)濾法是直接進(jìn)行數(shù)據(jù)訓(xùn)練并評(píng)估數(shù)據(jù)性能的方法，根據(jù)評(píng)估結(jié)果去除相關(guān)性小、冗余度高的數(shù)據(jù)，與分類(lèi)算法沒(méi)有關(guān)聯(lián)。封裝法和嵌入法都需要進(jìn)行后續(xù)的分類(lèi)計(jì)算，數(shù)據(jù)的維數(shù)越高，計(jì)算成本就會(huì)越大，不太適合小樣本數(shù)據(jù)特征的選擇。過(guò)濾法的評(píng)估函數(shù)是獨(dú)立的，在其評(píng)估標(biāo)準(zhǔn)中不會(huì)納入任何分類(lèi)器，選出的特征子集與特定的分類(lèi)算法無(wú)關(guān)，因此計(jì)算成本較低[3]。過(guò)濾法與另外兩種方法相比，計(jì)算也更加的高效。Kamatchi等對(duì)小樣本數(shù)據(jù)特征冗余性進(jìn)行考慮，同時(shí)結(jié)合特征類(lèi)型的區(qū)分能力，給出一致性度量的標(biāo)準(zhǔn)，若給定樣本之間的特征值相同，類(lèi)別也相同，則可以判斷樣本是一致的，以此為基礎(chǔ)進(jìn)行數(shù)據(jù)過(guò)濾[4]。Bernick等研究了過(guò)濾式特征選擇法，認(rèn)為過(guò)濾法可以對(duì)特征之間的關(guān)系、特征和類(lèi)型之間的關(guān)系進(jìn)行很好的度量，進(jìn)而使特征選擇變得更加有效[5]。本文研究了MIFS過(guò)濾式特征選擇算法，并結(jié)合Boruta算法進(jìn)一步拓展，實(shí)驗(yàn)證明本算法有效性較高。

1 MIFS特征選擇算法的基本步驟與拓展

1.1 MIFS特征選擇算法的基本步驟

對(duì)于小樣本數(shù)據(jù)來(lái)說(shuō)，特征選擇不僅要對(duì)特征和類(lèi)型之間的關(guān)聯(lián)性進(jìn)行考慮，還要考慮不同特征可能產(chǎn)生的冗余性，當(dāng)特征和類(lèi)型關(guān)聯(lián)度有較大差別時(shí)，需要進(jìn)一步避免冗余度的計(jì)算。根據(jù)以上問(wèn)題的考慮，本文采用MIFS（MI-haled feature selection）算法，根據(jù)小樣本數(shù)據(jù)度量特征和類(lèi)型的關(guān)系，首先按照兩者的關(guān)聯(lián)性進(jìn)行特征排序，然后在一定標(biāo)準(zhǔn)下將特征分組，從中找出所需的特征組成特征子集。

設(shè)特征子集的數(shù)據(jù)集所擁有的樣本數(shù)量為，特征維度的數(shù)量為，而特征則用1,2,…,a

表示，類(lèi)型用表示，用V表示a的值域，用V表示的值域。通過(guò)以上假設(shè)，a和的特征選擇指數(shù)(a,)計(jì)算公式如下：

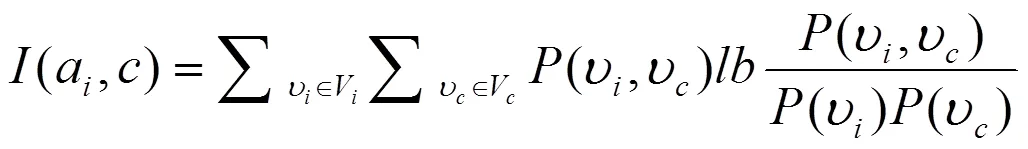
在上式中，(?,?)代表a取值?且取值?的概率，特征選擇指數(shù)(a,)值越大，特征與類(lèi)型之間的關(guān)聯(lián)程度就越高。根據(jù)式（1）依次計(jì)算每一個(gè)特征和類(lèi)型的特征選擇指數(shù)，然后按照特征選擇指數(shù)的大小，從高到低排序，并進(jìn)一步分組特征子集，依據(jù)的標(biāo)準(zhǔn)為，該值用以下公式計(jì)算：

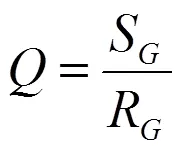
在上式中，代表一個(gè)特征組，S是和類(lèi)型的關(guān)聯(lián)度，R是里面全部特征的相似性。進(jìn)一步計(jì)算S和R：

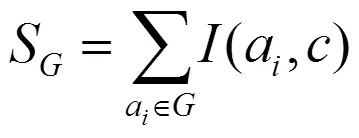
在上式中，里面的特征為a，a，(a,a)則是a和a的特征選擇指數(shù)，用以下公式計(jì)算：

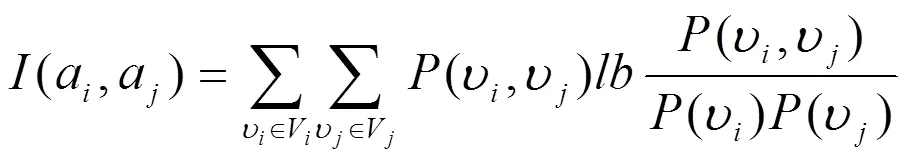
在上式中，(?,?)代表a取值?且a取值?的概率，特征選擇指數(shù)(a,a)值越大，說(shuō)明a與a越相似。同樣道理，的值越高，該特征組的特征和類(lèi)型關(guān)聯(lián)度就越大，而組內(nèi)各特征的冗余度就越小。反之亦然。為計(jì)算的初始值，需要在分組中放入2個(gè)通過(guò)選擇的特征：第一個(gè)特征是排在首位的1；第二個(gè)特征需要計(jì)算1和另外各特征a的特征選擇指數(shù)，得出特征選擇指數(shù)值最大的特征，該特征與1最為相似。最后根據(jù)式（2）對(duì)標(biāo)準(zhǔn)值進(jìn)行計(jì)算，記成0。

相對(duì)于另外的特征來(lái)說(shuō)，將排在首位的特征在分組中添加并計(jì)算值，若≤0，則說(shuō)明這個(gè)特征與其它特征有著較高的冗余度，這時(shí)需要進(jìn)一步添加下一個(gè)特征，對(duì)新值進(jìn)行計(jì)算并迭代，一直到>0為止，才停止添加特征。這時(shí)得到的特征組是第一個(gè)分組，沒(méi)有進(jìn)入該特征組的其它特征可以重復(fù)上面的步驟，產(chǎn)生新的一個(gè)特征組，最后目標(biāo)是全部特征都分配到相應(yīng)特征組內(nèi)。候選特征子集則由每一個(gè)特征組首個(gè)特征所組成。根據(jù)以上分析，MIFS算法的基本步驟如下：

輸入數(shù)據(jù)：特征子集的數(shù)據(jù)集、候選特征數(shù)。

輸出數(shù)據(jù)：候選特征子集S。

第1步：根據(jù)式（1）計(jì)算特征子集的數(shù)據(jù)集內(nèi)每一個(gè)特征和類(lèi)型的特征選擇指數(shù)(a,)；

第2步：根據(jù)特征選擇指數(shù)的大小，從高到底進(jìn)行排序，得出目標(biāo)特征集；

第3步：使=1，從特征集內(nèi)取出排首位的特征1，放進(jìn)特征組G；

第4步：根據(jù)式（3）對(duì)1和另外每一個(gè)特征a的特征選擇指數(shù)(a,a)進(jìn)行計(jì)算，取最大值特征放進(jìn)特征組G；

第5步：根據(jù)式（2）對(duì)G的值進(jìn)行計(jì)算，記成0。

第6步：從目標(biāo)特征集的剩余特征里，取排在首位的特征放進(jìn)特征組G，根據(jù)式（2）對(duì)G的值進(jìn)行計(jì)算，若≤0，重復(fù)第5步，若>0，當(dāng)前的特征組G即可作為首個(gè)分組；

第7步：使=+1，從目標(biāo)特征集的剩余特征里，繼續(xù)重復(fù)第3步到第6步，得出新特征組G，一直到=為止，或者目標(biāo)特征集的剩余特征全部被分配到特征組；

第8步：取每一個(gè)特征組的首個(gè)特征，放進(jìn)候選特征子集S；

第9不：返回候選特征子集S。

1.2 MIFS特征選擇算法的拓展

MIFS特征選擇算法雖然能夠利用特征分組逐步去除冗余特征，但與許多傳統(tǒng)型的過(guò)濾算法一樣，很難確定出最佳特征，這就需要進(jìn)一步拓展該算法，即將MIFS算法與其它能夠有效確定最佳特征的算法相結(jié)合。本文選取了Boruta算法進(jìn)行結(jié)合，形成一種新的MIFS-Boruta算法。Boruta屬于一種全覆蓋型的特征選擇算法，其優(yōu)勢(shì)在于信息預(yù)測(cè)，而不考慮關(guān)聯(lián)度的高低，能夠根據(jù)信息預(yù)測(cè)找出全部的相關(guān)特征，因此比較適合最佳特征的確定。

在MIFS-Boruta算法中，可以對(duì)過(guò)濾后的結(jié)果進(jìn)行充分利用，不斷提高算法的運(yùn)行效率，同時(shí)強(qiáng)化特征子集的分類(lèi)性能。MIFS-Boruta算法還能確定特征子集內(nèi)的特征數(shù)量，與過(guò)濾算法形成良好的互補(bǔ)。該算法的主要目標(biāo)是提升特征選擇算法的效果，能夠自動(dòng)選擇冗余度及維數(shù)更小的特征，以確定最佳特征，基本計(jì)算步驟如下：

輸入數(shù)據(jù)：特征子集的數(shù)據(jù)集、候選特征數(shù)、迭代數(shù)。

輸出數(shù)據(jù)：特征子集。

第1步：在中進(jìn)行MIFS計(jì)算，得出含有個(gè)候選特征的S；

第2步：從中取出S相對(duì)應(yīng)的數(shù)據(jù)組成新數(shù)據(jù)集D；

第3步：在D中進(jìn)行Boruta計(jì)算，迭代數(shù)為；

第4步：返回特征子集。

在MIFS特征選擇算法初始階段，會(huì)選擇與特征選擇指數(shù)最接近的特征放入最新特征組中，并作為各特征組的代表，被選為最優(yōu)特征子集中的候選特征。這時(shí)需要通過(guò)Boruta算法從這些候選特征里面除去一些次要的特征，但是特征選擇指數(shù)值最高的特征有著很強(qiáng)的分類(lèi)效果，這樣的特征不會(huì)被除去，而會(huì)在最優(yōu)特征子集中得到保留。

2 結(jié)果與分析

2.1 實(shí)驗(yàn)數(shù)據(jù)

為驗(yàn)證本文算法在高緯度小樣本數(shù)據(jù)中的有效性，選擇了9個(gè)公開(kāi)的數(shù)據(jù)集，所有特征的維數(shù)在1024~18847之間，平均維度為7297，有5個(gè)數(shù)據(jù)集的維數(shù)大于5000，有2個(gè)數(shù)據(jù)集的維數(shù)大于10000，主要類(lèi)型是圖像數(shù)據(jù)和生物學(xué)數(shù)據(jù)，如表1所示。

2.2 各算法特征選擇的結(jié)果對(duì)比

為驗(yàn)證本文算法能否得到更好的特征選擇結(jié)果，引入ICAP、CMIM、CIFE三種較為典型的特征選擇算法，都屬于傳統(tǒng)的過(guò)濾式算法。為了使對(duì)比公平，在實(shí)驗(yàn)里分別將這三種算法結(jié)合Boruta算法，在每一個(gè)樣本集中設(shè)定好候選特征數(shù)量，各算法最終選擇出來(lái)的特征個(gè)數(shù)如表2所示。實(shí)驗(yàn)結(jié)果表明，任何一種算法的特征選擇數(shù)都低于原始特征的維度，而在9個(gè)數(shù)據(jù)集中，MIFS-Boruta算法有6個(gè)數(shù)據(jù)集的特征數(shù)最多，體現(xiàn)了更廣的特征選擇量。

表 1 實(shí)驗(yàn)數(shù)據(jù)統(tǒng)計(jì)

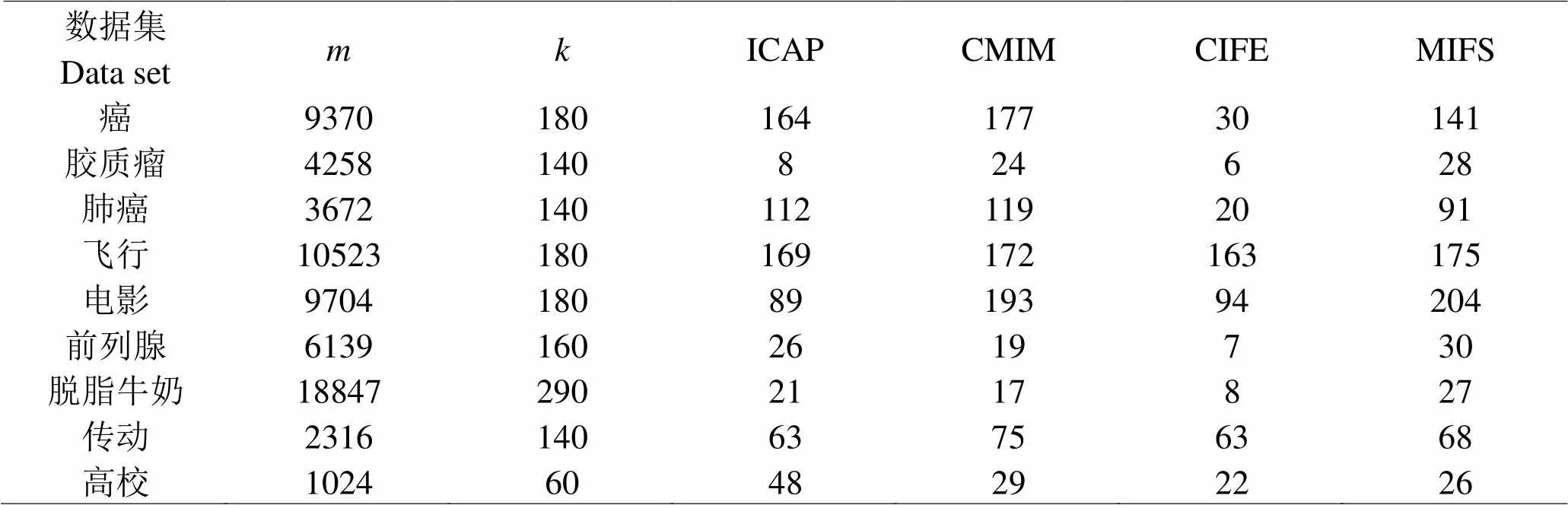
表 2 不同算法組合Boruta得出的特征選擇結(jié)果

2.3 各算法特征子集的分類(lèi)性能對(duì)比

為驗(yàn)證本文算法對(duì)于特征選擇的有效性，依然以ICAP、CMIM、CIFE三種較為典型的特征選擇算法作對(duì)比，分別在支持向量機(jī)監(jiān)督學(xué)習(xí)模型上進(jìn)行計(jì)算，實(shí)驗(yàn)采用以下2個(gè)指標(biāo)驗(yàn)證性能：（1）最低分類(lèi)錯(cuò)誤率；（2）平均最低分類(lèi)錯(cuò)誤率。對(duì)比結(jié)果如表3所示。MIFS算法共有7個(gè)數(shù)據(jù)集的最低分類(lèi)錯(cuò)誤率最低，而且平均最低分類(lèi)錯(cuò)誤率也是最低，相對(duì)于其它算法來(lái)說(shuō)有著良好的表現(xiàn)。

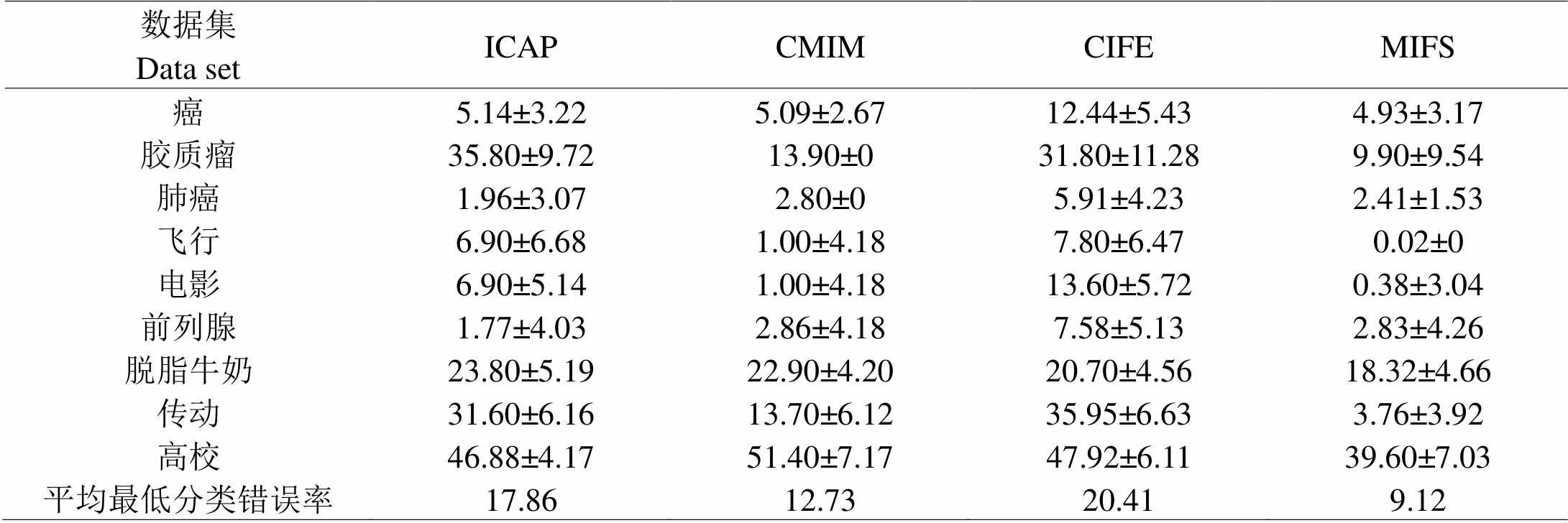
表 3 不同算法在支持向量機(jī)上的分類(lèi)錯(cuò)誤率統(tǒng)計(jì)（%）

3 討論

小樣本理論創(chuàng)始于十九世紀(jì)初，在區(qū)間估計(jì)和統(tǒng)計(jì)假設(shè)檢驗(yàn)等領(lǐng)域得到廣泛應(yīng)用。小樣本統(tǒng)計(jì)省錢(qián)省力，極大地節(jié)約了計(jì)算的時(shí)間，不僅受到統(tǒng)計(jì)學(xué)家的歡迎，還被工業(yè)、農(nóng)業(yè)、科學(xué)研究等領(lǐng)域的工作者所重視。從此次實(shí)驗(yàn)結(jié)果看，本文提出的算法在高緯度小樣本數(shù)據(jù)中的特征選擇較為有效，能夠取得更好的特征選擇結(jié)果。Ekiz等認(rèn)為小樣本數(shù)據(jù)的特征維數(shù)較多，而且具備冗余特征，可以利用特征選擇的方法降低數(shù)據(jù)維數(shù)[6]。Brewer等提出一種面向高維數(shù)據(jù)的迭代式特征選擇方法，主要是改進(jìn)了Lasso方法，實(shí)驗(yàn)結(jié)果表明，該方法可以較好地選擇高維小樣本數(shù)據(jù)集特征，屬于當(dāng)前比較有效的特征選擇法[7]。Dahl等基于粒計(jì)算角度，提出一種粒化——融合框架下的高維數(shù)據(jù)特征選擇算法，首先將原始數(shù)據(jù)集粒化成小規(guī)模的數(shù)據(jù)子集，并在每一個(gè)粒上建立起若干個(gè)套索模型，從而實(shí)現(xiàn)粒特征的選擇，然后根據(jù)權(quán)重情況融合各粒特征的選擇結(jié)果[8]。

4 結(jié)論

本文針對(duì)小樣本數(shù)據(jù)特征選擇問(wèn)題，采用MIFS算法進(jìn)行特征分組計(jì)算，選出最大相關(guān)性的特征，降低數(shù)據(jù)集維度。為解決最佳特征難以確定的問(wèn)題，拓展了MIFS算法，提出一種MIFS-Boruta算法，在降低數(shù)據(jù)集維度的基礎(chǔ)上，還能確定出最佳特征的子集。通過(guò)實(shí)驗(yàn)分析，驗(yàn)證了該算法的有效性。但是該算法涉及到的候選特征數(shù)量，需要通過(guò)人工方式進(jìn)行設(shè)定，若數(shù)值偏大將會(huì)對(duì)最終的特征選擇效率造成一定影響，若數(shù)值偏小則會(huì)對(duì)選出的特征性能造成影響，所以這方面還有待于進(jìn)一步研究。

[1] Ditlevsen O. Baysian estimation of(>) from a small sample of Gaussian data[J]. Structural safety, 2017,68(4):110-113

[2] Lunardon N, Scharfstein D. Comment on "Small sample GEE estimation of regression parameters for longitudinal data"[J]. Statistics in medicine, 2017,36(22):3596-3600

[3] McNeish DH, Jeffrey R. Correcting Model Fit Criteria for Small Sample Latent Growth Models With Incomplete Data [J]. Educational and Psychological Measurement, 2017,77(6):990-1018

[4] Kamatchi PMK, Kavitha DSN. Data analytics: feature extraction for application with small sample in classification algorithms[J]. International journal of business information systems, 2017,26(3):378-401

[5] Bernick CB, Guogen SS. Sample size determination for a matched-pairs study with incomplete data using exact approach[J]. The British journal of mathematical and statistical psychology, 2018,1(1):60-74

[6] Kirubavathi G, Anitha R. Structural analysis and detection of android botnets using machine learning techniques[J]. International Journal of Information Security, 2018,17(2):153-167

[7] Brewer RP, John HM. A Critical Review of Discrete Soil Sample Data Reliability: Part 2-Implications[J]. Soil & Sediment Contamination, 2017,26(1):23-44

[8] Dahl JB. Mathiesen O, Karlsen APH. Evolution of bias and sample size in postoperative pain management trials after hip and knee arthroplasty[J]. Acta Anaesthesiologica Scandinavica, 2018,62(5):666-676

MIFS Filtering Feature Selection Algorithm for Small Sample Data

WANG Bo, LI Shi-hui, ZHENG Peng-fei

322000

Aiming at the problem of feature selection for small sample data and the difficulty of determining the best feature, a MIFS filtering feature selection algorithm was proposed, which combined Boruta algorithm to reduce the dimension of data set and determine the subset of the best feature. Through the experimental results and analysis, comparing with the other three traditional filtering algorithms, the effectiveness of the proposed algorithm was verified. The results showed that MIFS-Boruta algorithm had broader feature selection and the lowest average classification error rate.

Small sample; NIFS; algorithm

TP301.4

A

1000-2324(2019)01-0145-05

10.3969/j.issn.1000-2324.2019.01.033

2018-03-26

2018-05-04

浙江省自然科學(xué)基金:具有公共自行車(chē)子網(wǎng)的城市公交網(wǎng)絡(luò)建模與優(yōu)化研究(LY17F030016)

王波(1982-),男,博士,副教授,主要研究方向?yàn)樽詣?dòng)化技術(shù)、計(jì)算機(jī)技術(shù). E-mail:52672026@qq.com