基于隱馬爾可夫模型路徑規劃方法

鄧旭 趙連軍 郇靜

摘要：針對復雜迷宮環境的目標體具體位置與路徑規劃問題為對象，提出了一種基于隱馬爾可夫模型的粒子濾波算法。該方法通過隱馬爾可夫模型的概率計算、粒子濾波算法時間流逝、觀察、抽樣策略，推理出目標體可能范圍，通過A·算法將目標捕獲。仿真結果表明，與普通的概率計算目標體位置，粒子濾波算法計算的目標體位置，大大減少了總步數，形成了最短路徑。

關鍵詞：路徑規劃：隱馬爾可夫模型：粒子濾波

0引言

人工智能在越來越多的領域得到了應用。近幾年人工智能的發展異常迅猛。Hinton等的卷積神級網絡在計算機視覺領域的圖形分類做出了重要貢獻，并且在2015優化成深度學習。

Silver，D等在2016使用深度神經網絡在有監督算法下訓練的AlphaGo戰勝韓國棋手李世石。AlphaGo Zero則實現了更進一步的提升，在不使用人類知識的情況下學習到了一個超人水平的計算機圍棋程序。

人工智能在迷宮搜索方面有著廣泛的應用。但是，自主移動機器人如何在未知的、復雜的環境中自主規劃從起點到終點的路徑，并且躲避障礙，或者通過路徑規劃捕獲具體目標始終是復雜的技術難題。因此，進行移動機器人路徑規劃算法的研究，具有一定的理論意義和工程應用意義。迷宮機器人是移動機器人的典型應用，也是檢驗路徑規劃算法較好的平臺

目前，在迷宮搜索方面，取得了很多有效的進展。但是目前的Agent迷宮搜索都是靜態的單個目標搜索。在多個動態目標搜索方面存在著明顯不足。

隱馬爾可夫模型是統計模型。用來描述含有隱含未知參數的馬爾可夫過程。其難點是從可觀察的參數中確定該過程的隱含參數。利用這些參數作進一步的分析。其在語音技術和手寫字符識別應用中廣泛使用，但在迷宮搜索領域用得較少。

通過隱馬爾可夫模型的應用，可以有效地確認多個動態目標位置，通過A*算法尋找和捕獲目標。

1 研究現狀

李慶中等提出的基于遺傳算法，簡單、有效的移動機器人實時動態避障路徑規劃方法，利用遺傳算法實時、穩定地進行動態路徑規劃。仿真實驗表明：動態路徑規劃方法可實時、穩定地產生移動機器人運動的最佳局部規劃路徑，且具有良好的動態避障性能。

顧新艷等研究移動機器人利用柵格法創建環境地圖時，在其計算資源有限的情況下，比較利用迷宮八方向搜索思想，實現最短路徑規劃的Dijkstra算法，提出采用基于柵格劃歸地圖的A*算法，能更快實現移動機器人的無碰最短路徑規劃。

溫如春等對傳統蟻群算法收斂性較慢的問題進行了改進。通過計算機仿真和電腦鼠機器人實際行走實驗表明，在場地復雜的情況下，該算法可以有效地規劃出全局最優路徑。

李道新等研究移動機器人的歷史與現狀基礎上，重點在移動機器人避障與路徑選擇規劃中常用的算法中選取柵格法、勢場法、遺傳算法等方法進行分析比較：并以自行設計的一款微型機器人為例，探討了基于紅外感知的未知環境特征提取方法和安全避障距離選取的原則，給出了一種深廣結合算法的移動機器人避障策略：描述了深廣結合算法在機器人迷宮地圖中最優路徑規劃實現中的應用。

Shazhaev Ilman（伊勒曼）基于多NAO機器人搭建實驗平臺，研究了機器人的定位模型、路徑規劃和走迷宮尋徑問題。根據所建立的圖像處理方法和定位模型得到了相應的圖形信息，利用圖像處理技術，完成了位置特征和環境特征的識別。基于NAO機器人坐標系，獲取環境特征的定位信息，通過定位實驗，驗證了定位模型和路徑規劃的可行性。基于建立的典型迷宮結構圖，進行了多機器人協同迷宮尋徑的研究。實驗完成了多機器人之間的信息交換，并可實時分享周圍的環境信息。建立了相應的算法，根據編制的程序，利用分享的信息，機器人可以決定如何在迷宮中進行下一步行動。由于決策信息的實時共享，多個機器人比單個機器人更高效快捷地走出迷宮。

2 實驗方法

本實驗通過隱馬爾可夫模型的粒子濾波算法和A*算法在復雜迷宮環境下找到動態目標。

2.1 馬爾科夫鏈

馬爾科夫鏈為狀態空間中。經過從一個狀態到另一個狀態的轉換的隨機過程。該過程要求具備“無記憶”的性質：下一狀態的概率分布只能由當前狀態決定，在時間序列中與前面的事件均無關。這種特定類型的“無記憶性”稱作馬爾可夫性質。在馬爾可夫鏈的每一步，系統根據概率分布，可以從一個狀態變到另一個狀態，也可以保持當前狀態。狀態的改變叫做轉移，與不同的狀態改變相關的概率叫做轉移概率，如隨機漫步就是馬爾可夫鏈的例子。隨機漫步中每一步的狀態是在圖形中的點。可以移動到任何一個相鄰的點。在這里移動到每一個點的概率都是相同的（無論之前漫步的路徑如何）。

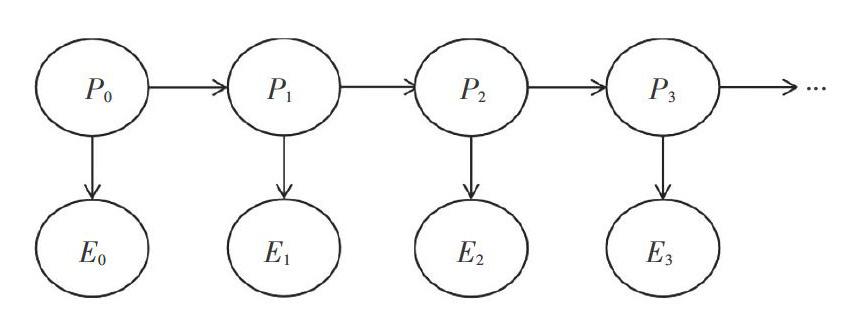
實驗為了追蹤所考慮的粒子隨時間的變化。需要了解馬爾科夫鏈的含義。其是在時間t=0的初始分布，以及某種過渡模型，用于描述在時間步長之間從一種狀態遷移到另一種狀態的可能性。如圖l所示馬爾可夫模型的初始分布，由Pr（P₀）給出的概率，從狀態i到i+1的轉變模型由Pr（P_i+1|P_i）給出。此過渡模型暗示的值是有條件的，其僅取決于P_i的值。換句話說，在時間t=i+1時的粒子位置滿足馬爾可夫性質或無記憶性，并且與除t=i以外的所有其它時間步長的粒子位置無關。如果用以下方法重建p₀，p₁，p₂之間的聯合，使用馬爾可夫模型鏈式規則如下：

Pr（P₀，P₁，P₂）=Pr（P₀）Pr（P₁|P₀）Pr（P₂|P₁，P₀），（1）

假設Markov屬性為true，并且W0W2| W1成立，則聯合簡化為：

Pr（P₀，P₁，P₂）=Pr（P_n）Pr（P₁|P₀）Pr（P₂|P₁）。（2）

馬爾科夫模型中，通常做出的最后一個假設是過渡模型是固定的。換句話說，對于所有i值，Pr（P_i+1|P_i）是相同的。在此可以用兩個表來表示馬爾可夫模型：一個用于Pr（P_n），一個用于Pr（P_i+1|P_i）。

通過馬爾可夫模型，看到了如何通過一系列隨機變量，將隨著時間的變化納入其中。例如，若想知道第1步的位置，可以從初始分布Pr（P₀）開始，并在過渡模型中使用小前向算法計算Pr（P₁₀）。但在時間t=0和t=10之間，可能會收集新的位置信息，這些證據可能會影響對任何給定位置概率分布的看法。

2.2 隱馬爾可夫模型

與馬爾科夫鏈不同。隱馬爾可夫模型有兩種不同類型的節點。為了區別起見，將每個pi稱為狀態變量，并將每個E_i稱為證據變量。由于pi是第i步的位置概率分布，自然得出第i步的具體位置，有條件地依賴于這一概率。馬爾科夫鏈如圖1所示。正如馬爾可夫模型一樣。隱馬爾可夫模型假設過渡模型是平穩的，具體模型如圖2所示。隱馬爾可夫模型對傳感器模型做出了Pr（P_i+1|P_i）額外的簡化，假設Pr（E_i+1|P_i）也是固定的。因此，任何隱馬爾可夫模型都可以用3個概率表來緊湊地表示：初始分布、過渡模型和傳感器模型。作為符號的最后一點，將定義時間i的概率分布，并給出所有證據E_i，…，E_i，且觀察至B（P_i）=Pr（P_i|E₁，…，E_i）。

同樣，將B₀（P_i）定義為在時間i處的概率分布，并觀察到證據E₁，…E_i，B（P_i）=Pr（P_i|E₁，…，E_i）將E_i定義為在時間步i觀察到的證據，有時會用以下形式重新表達時間步1≤i≤t的證據匯總：E_1：t=E₁，…E_t，在這種表示法下，Pr（P_i|E₁，…E_i）。經過時間的更新，將新的證據迭代地納入粒子模型中。

2.3粒子濾波算法

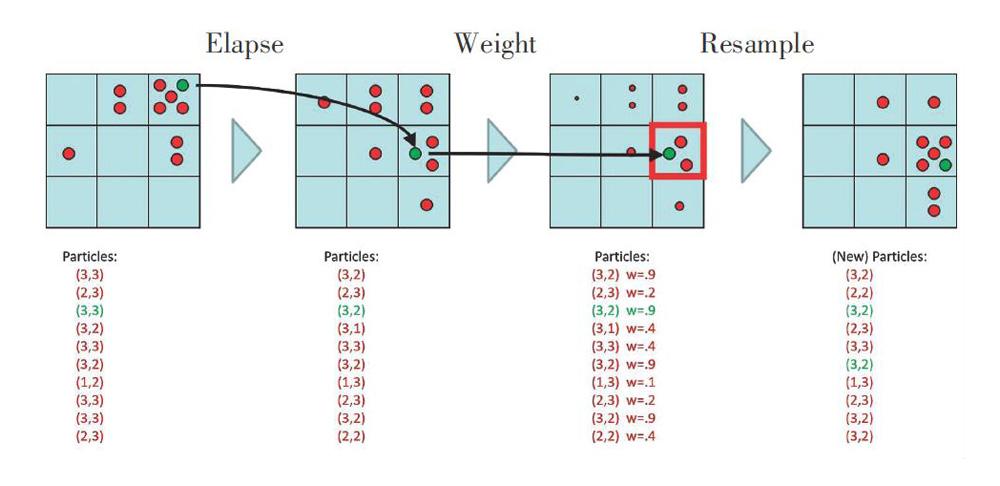
對于貝葉斯網絡，使用一種采樣技術是有效估算所需概率分布的可行選擇。隱藏的馬爾可夫模型具有相同的缺點一運行需要時間。貝葉斯凈采樣的過程稱為粒子濾波，其涉及模擬一組粒子的運動，通過狀態圖來近似表述隨機變量的概率（信度）分布。

粒子過濾模擬始于粒子初始化，可以隨機地、均勻地或從一些初始分布中采樣粒子。一旦對初始粒子列表進行了采樣，在每個時間步進行觀察更新，更新是根據過渡模型，更新每個粒子的值。處于狀態P_i的粒子，可從Pr（P_i+1|P_i）給出的概率分布中采樣，得到更新后的值。更新與使用貝葉斯網絡進行采樣的相似性，因為任何給定的粒子的頻率反映了轉移概率。

使用傳感器模型Pr（E_i|P_i），根據觀察到的證據所指示的概率和粒子的狀態對每個粒子進行加權。對于狀態為P_i且傳感器讀數為E_i顆粒，分配Pr（E_i| P_i）的權重。觀測更新的算法如下：

（1）如上所述計算所有顆粒的權重。

（2）計算每種狀態的總權重。

（3）如果所有狀態的所有權重之和為0，重新初始化所有粒子。

（4）否則，標準化總權重分布，并從該分布重新采樣粒子列表。注意觀察更新與似然加權的相似性，在此根據證據再次降低樣本的權重。具體過程如圖3所示。

3 實驗結果與分析

3.1實驗設置

為了驗證實驗的有效性，文本為Agent的路徑規劃設置了虛擬環境。本文制造了不同大小阻礙環境，其中障礙物和目標點都是隨機生成的。如圖4所示，實驗設置了7個障礙，1個Agent，2個不可見目標點的7×7大小的原始環境地圖。

由于實驗的目標體是不可見的，通過粒子來代替一個具體個體，通過隱馬爾可夫模型的粒子濾波算法找到不可見點的具體位置，如圖5所示。

如圖6所示，當粒子向不可見的點合攏時，智能體能找到具體目標，通過A*算法直接找到最近不可見的點，再找到另外一個不可見的點。

3.2 實驗結果

為了使實驗結果具有更好的準確性，將實驗分成3組，分別在小迷宮、中迷宮、大迷宮的環境下尋找2個不可見目標點，通過10次實驗，取其均值，其結果見表1.

通過實驗結果可見，基于粒子濾波算法的路徑規劃比概率計算的路徑規劃，效率大幅度提升。

4 結束語

通過對復雜迷宮環境下的Agent尋找不可見目標的研究，提出了一種基于隱馬爾可夫模型的粒子濾波算法，Agent通過粒子濾波算法確認不可見目標，通過A*算法最短路徑找到最近目標。本實驗使用粒子濾波結合A*算法，比普通的概率計算結合A*算法效率更高。下一步將研究多個智能體協同合作，實現多智能體在復雜環境下合作路徑規劃。