基于SPSS加權回歸的回歸分析條件適用性研究

曹玉茹

（上海對外經貿大學 統計與信息學院，上海 201620）

0 引言

在統計學中，線性回歸是利用最小平方函數對一個或多個自變量和因變量之間關系進行建模的一種回歸分析。這種函數是一個或多個稱為回歸系數的模型參數的線性組合。只有一個自變量的情況稱為簡單回歸,大于一個自變量情況的叫做多元回歸。

線性回歸模型經常用最小二乘逼近來擬合，但線性回歸的前提條件無法滿足時，也可能用別的方法來擬合。線性回歸雖然有廣泛的使用，但其適用條件也非常嚴格，很多時候大家在使用線性回歸時并未過多考慮其條件是否滿足，因此估計量不具備最佳線性無偏特性，從而可能造成預測準確度不夠，甚至于出現錯誤的預測，尤其在多元回歸中，隨著自變量的數量增加，擬合優度調整的R2也會增大[1]，但很有可能是由于自變量的自相關性造成的偽回歸導致的結果，而并非就說明模型擬合程度好。且如果殘差為異方差序列，則在不同的X取值處，Y的實際分散程度不同，則回歸線的預測在不同的X點準確度不同，回歸預測效果不穩定，或者說此時在不同的X水平，其與Y的關系是有很大差別的，無法用單一的回歸方程去預測Y。此時的回歸分析可能失效，從而無法進行準確的預測問題。如何得到相對準確的、穩定的預測模型是學者們一直致力研究的問題。然而最基本的問題當然是必須要滿足以下的回歸分析的基本條件：（1）自變量與因變量間存在線性關系。（2）殘差序列獨立。（3）殘差分布是均值為0的正態分布。（4）殘差序列是方差齊性的。本文通過具體的示例主要圍繞著回歸分析條件檢驗方法及其相關的處理方法展開研究，著重研究異方差的檢驗方法及其應對措施。

1 異方差檢驗

由文獻[2]可知，無論自變量x取怎樣的值，對應殘差的方差都應該相等，他不應隨解釋變量或被解釋變量的取值的變化而變化，否則就出現了異方差現象。當存在異方差時，參數的最小二乘估計不再是最小方差的無偏估計，不再是有效性估計；容易導致回歸系數顯著性檢驗的t值偏高，從而容易拒絕原假設，使那些不該保留的變量保留下來了，使得最終模型的預測偏差較大。下面通過具體的示例來說明異方差的檢驗方法。

本文利用SPSS自帶的數據polishing.sav為例分析說明產品半徑能否預測產品拋光時間問題。首先用線性回歸做散點圖及簡單線性回歸，并對殘差做進一步檢驗得到結果見圖1、圖2所示。

圖1 加擬合線的散點圖

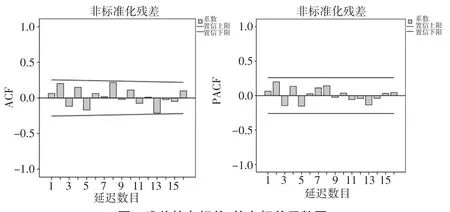
圖2 殘差的自相關、偏自相關函數圖

表1 模型匯總表b

表2 方差分析表b

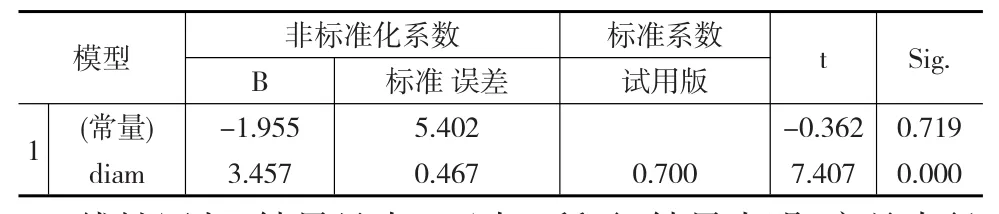
表3 系數a（回歸統計表）

線性回歸，結果見表1至表3所示，結果表明：產品半徑確實對拋光時間產生影響顯著影響，雖然擬合優度不高，但回歸方程及回歸系數的顯著性都通過檢驗；而且通過散點圖可知單個產品對象的擬合效果很不錯，甚至R2達到0.876，因此有理由進一步具體分析變量半徑和拋光時間之間存在的關系。由簡單線性回歸得到產品半徑與拋光時間的回歸方程為：

從前面的分類散點圖可以看出，這個方程預測準確度可能有問題，而且總體的擬合優度0.49也不是很高。因此本文考慮做進一步的分析。

鑒于前面提到的回歸模型的適用條件要求殘差具備正態性、獨立性和方差齊性的特點。考慮到可能是回歸的適用性條件不滿足造成的回歸方程有問題。一方面通過SPSS回歸分析自帶的DW參數（本例中為1.858）初步判斷殘差獨立，進一步利用時間序列分析工具[3]得到殘差的自相關函數圖（見圖2）基本可以認為殘差是獨立的；再通過非參數檢驗單樣本K-S檢驗，K-S統計量對應的伴隨概率明顯大于0.05基本斷定殘差是正態分布的，結果如表4所示。

表4 單樣本K-S檢驗

至此，回歸分析的前三個條件是得到滿足了，但為什么回歸分析的結果不滿意呢，很可能第四個條件出問題了。根據預測值的殘差分布圖發現殘差可能存在異方差現象，進一步根據殘差和預測變量的等級相關檢驗結果[4]說明確實存在異方差現象，等級相關檢驗的具體方法是先求出殘差和預測變量，將殘差求絕對值后和預測變量一起轉成秩變量，再利用SPSS相關分析求出Speaman等級相關系數。

結果表明：由伴隨概率值sig=.001＜0.05得出，殘差的秩和預測值的秩之間存在顯著的相關性,也即進一步證明殘差確實存在顯著異方差現象，檢驗見圖3所示。

圖3 殘差的異方差檢驗

其中圖3表示回歸的標準化預測值與標準化殘差的散點圖，表5為等級相關分析的分析結果。

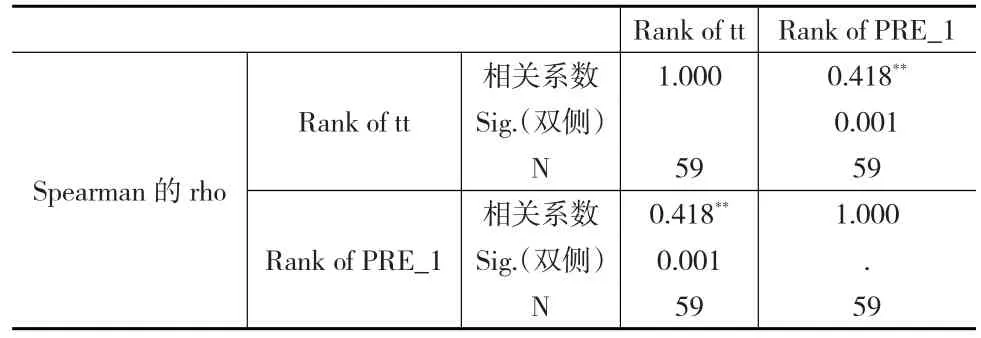
表5 等級相關分析結果

至此得到上面的回歸模型違背了基本的適用條件，原來的回歸方程（公式1）可能無法準確的預測結果，需要重新構建回歸模型。

2 加權線性回歸分析

上面的回歸模型的失效原因是異方差造成的，進一步如何去除回歸中的異方差現象呢？利用SPSS軟件中的加權最小二乘法估計法得到回歸加權變量，再利用加權變量完成回歸分析的方法，可以大大緩解殘差的異方差現象，從而得到較為精確的回歸模型。根據文獻[5]，可以先對解釋變量實施方差穩定變換后再進行回歸參數的估計，本文嘗試利用Spss中的加權回歸得到加權變量，再利用加權變量作為回歸分析中的加權最小二乘變量得到新的加權回歸模型（公式2）及其對應的檢驗結果如下：

Time=0.691+3.208*diam （2）

經過加權回歸分析，結果見表6至表8所示。結果表明：雖然擬合優度有些許降低，但估計的標準誤差降低非常明顯；且回歸方程及回歸系數的顯著性均通過檢驗；殘差的自相關函數圖（見圖4）基本可以認為殘差是獨立的；通過非參數檢驗單樣本K-S檢驗，K-S統計量對應的伴隨概率明顯大于0.05基本斷定殘差是正態分布的，結果如表9所示。

表6 模型匯總表

表7 方差分析表

表8 回歸統計表

利用加權變量得到新的殘差和新的預測變量，將殘差求絕對值后和預測變量一起轉成秩變量，再利用相關分析求出Speaman等級相關系數，由伴隨概率值sig＞0.05得出，相關性不顯著,即殘差的異方差現象確實消除，檢驗見圖5、表10所示。

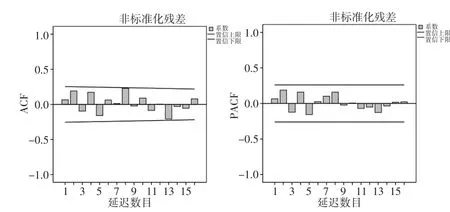
圖4 新模型殘差的自相關、偏自相關函數圖

表9 單樣本Kolmogorov-Smirnov檢驗

圖5 異方差檢驗

表10 異方差檢驗（等級相關分析）表

表示加權后的標準化預測值和標準化殘差。

鑒于以上分析，新的模型通過了回歸分析的異方差條件檢驗，且估計誤差大大縮小，新的模型可能相比原先的模型更適合進行預測分析使用。

又通過SPSS的探索性分析得到time變量的樣本數據分布非正態，見表11所示。

表11 正態性檢驗結果

因此可以先進行正態化處理[6]后再進行回歸分析，結果見下頁表12、表13所示。

其他過程如上面的加權處理過程，此處省略，結果發現：模型估計誤差進一步縮小，擬合優度也有所改善，效果可以更好。

表12 正態化之后的回歸結果（模型匯總b,c）

表13 三種模型估計指標匯總對比

雖然估計誤差得到改善，而且回歸條件也都通過檢驗，但是擬合優度還是不盡如人意，究其原因，可以發現在本文開頭的散點圖中可能不同類別的產品拋光時間的變化是不相同的，因此，本文考慮分別討論不同種類對象的回歸情況。SPSS中可以通過拆分文件再分析的方法得到分析結果，結果如表14。

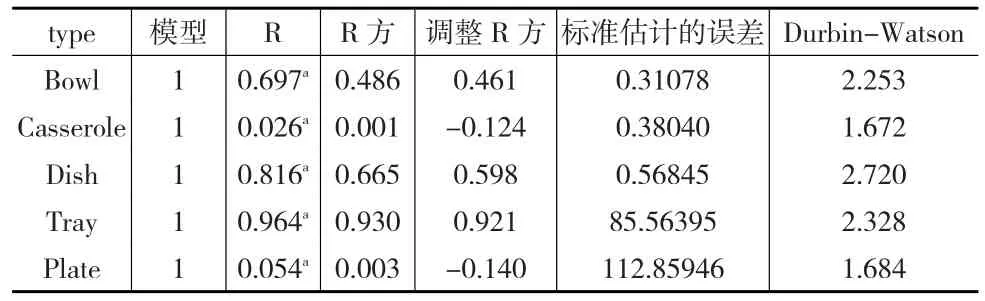
表14 模型摘要表

顯然，不同類別的對象其回歸結果差異很大，對于產品Casserole和Plate非常不適合使用半徑來預測其拋光時間，而Tray卻效果非常好，相應的檢驗也都能通過，此處不再贅述。

3 結論

回歸分析廣泛應用于計量經濟和金融數據分析領域，主要用來對各種經濟現象和金融現象進行預測，雖然對于回歸模型的檢驗有很多指標和方法，但回歸模型的前提條件是否滿足可能會直接導致模型的準確性，因此為了得到更加優化、合理的回歸模型進行預測，本文從回歸模型的適用性條件是否滿足入手，借助于各種常規檢驗方法并結合時間序列中的自相關和偏自相關函數圖示對實際案例中的回歸適用性條件給出了新的檢驗方法，并利用SPSS軟件中的加權最小二乘工具得到回歸中的權重變量，消除了回歸模型中的異方差，進一步修正了原來的回歸模型，并結合SPSS中的分類散點圖技術為原來的分析尋求到一個更加合適的回歸模型。