基于幾何距離準則的彈道外推方法
, ,
(1.中國電子科技集團公司第三十八研究所, 安徽合肥 230088;2.孔徑陣列與空間探測安徽省重點實驗室, 安徽合肥 230088)
0 引 言
彈道導彈自問世以來,以其射程遠、威力大、精度高、機動性好和生存能力強等優越性,成為戰爭中極具價值的武器系統,尤其海灣戰爭以后,受到世界各國高度重視[1]。應運而生的導彈防御成為各國軍事研究不可規避的任務。
關機后,彈道導彈所受空氣阻力很小,主要依靠慣性飛行,因此其飛行軌道在理論上是完全確定的。對一組雷達量測數據作平滑優化,選取合適的初值,從而外推出彈道導彈的軌道,是預警、制導等雷達軟件系統的關鍵技術之一。
當前使用較多的彈道外推算法,一類是基于彈道導彈的動力學方程,使用數值法一步一步進行外推[2];另一類是采用解析法[3],求出一組軌道參數,從而求解整個彈道。從理論上,在選取合適步長的情況下,數值法可以達到很高的外推精度,而軌道解析法的精度相對較低,但計算速度較數值法要快。無論是數值法還是解析法,它們的外推精度都極大地依賴于初始點的位置和速度信息的準確性。初始點的選取方法應用比較廣的有兩種:一種是直接濾波[4-5],取濾波的最后一點為初始點;另一種是用最小二乘法分別在X,Y,Z三個維度上對量測數據進行平滑,取平滑后的中點為初始點[6]。此外,還有一些方法是在這兩種方法的基礎上作一些調整和組合[7-9]。濾波方法使用了彈道導彈動力學方程,最小二乘法是對彈道作數學近似。然而,彈道導彈作為一種特殊的雷達觀測目標,其運行軌道理論上是可完全確定的。但是,上述方法都沒有利用到彈道的這種獨特特性。
針對上述情況,本文在充分研究彈道導彈軌道特性的基礎上,設計并實現了一種基于三維空間幾何距離準則的彈道外推方法,對初始點的位置和速度信息進行優化。該方法基于在地球慣性坐標系中,標準彈道為位于過地球質心的一個三維平面內的橢圓這一事實,先確定橢圓平面,使所有量測點到該平面的幾何距離平方和最小,然后用各量測點在平面內的投影點代替原始點跡進行最小二乘法平滑,取所有平滑點中點為初始點,進行彈道外推。應用STK軟件進行彈道仿真試驗,分別使用最小二乘法和基于幾何距離準則的方法對量測數據作平滑,選取合適的初始點進行彈道外推,結果表明,該方法的外推精度有顯著提高。
1 基于幾何距離準則的彈道外推方法
彈道導彈由于飛行時間短,可以忽略其軌道攝動,將其彈道看作是繞地球質心的二維橢圓軌道運動。在以地球質心為原點的慣性坐標系(Earth-Centered Inertial,ECI)下,彈道導彈的運動規律滿足開普勒定律[10]:1)彈道目標的運行軌道是一個橢圓,地球質心與橢圓的一個焦點重合;2)在相同時間內,彈道目標與地球質心的連線掃過的面積相等;3)彈道目標運行周期的平方與其運行軌道的橢圓長半軸的三次方成正比,比值為地心引力常數的倒數。
根據開普勒定律,可以推導出彈道目標的運行軌道為位于一個過地球質心的平面內的橢圓[7-8]。根據幾何知識,彈道目標的橢圓軌道可由以下兩步來確定:1)計算軌道所在的平面,使得地球質心位于平面內;2)確定彈道軌道所在的三維橢球體,橢球體的兩個焦點都位于第1)步確定的平面內。計算所得的平面和橢球體的交線即為彈道目標的軌道。軌道確定后,彈道目標在任一時刻的位置和速度都可以計算出來。反過來,知道彈道目標在某一時刻的位置和速度,就可以外推出整條軌道。因此,用來計算的這一時刻的位置和速度信息的準確性十分重要。
基于幾何距離準則的彈道外推方法分為兩步:
1) 通過雷達的一組量測值估算出彈道目標的軌道;
2) 取軌道中點為初始點,用數值法進行彈道外推。
1.1 軌道計算
軌道計算的方法是先確定彈道平面,再在平面內計算橢圓的方程。計算中,采用J2000地心慣性坐標系。
1.1.1 計算彈道平面
考慮t1,t2,…,tn時刻的量測數據Xn={Xi},Xi=[xiyizi]′,i=1,2,…,n。由于彈道目標軌道所在的平面經過坐標系原點(地球質心),可設該平面的方程為a1x+a2y+a3z=0,其中a1,a2,a3為待求參數。
由于隨機誤差的存在,雷達量測點不會嚴格在一個平面內,但偏離理論彈道平面不會太遠,因此需要擬合一個平面,使所有量測點到擬合平面的距離平方和最小。擬合平面即為待求的彈道平面[11]。
量測點Xi到擬合平面的距離為
(1)
對上式作變換,令
(2)

(3)
則式(1)化為
(4)
擬合平面方程化為
(5)
t1,t2,…,tn時刻的量測點到擬合平面的距離平方和為
(6)
(7)
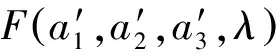
(8)
將式(7)代入,化簡得
(9)
定義系數矩陣A:
(10)
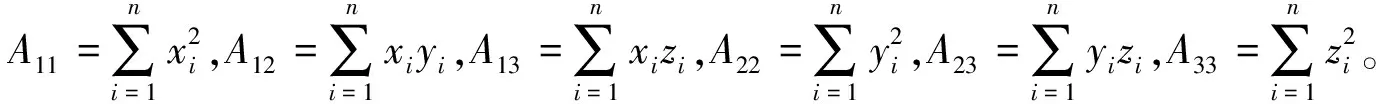
式(9)中方程組的前3個方程可表示為
(11)
1.1.2 野值判定準則
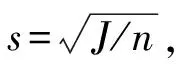
|di|<δs
(12)
對每個量測點進行判別,如果上式成立,則判定該量測點為正確值,反之,則判定為野值。δ的取值根據實際情況來選取,經驗表明3或者4是不錯的選擇。
1.1.3 理論彈道計算
(13)
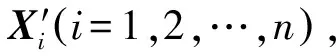
綜上所述,彈道目標理論軌道的算法可表示如下:

2) 計算量測點到平面的距離的標準差s;
3) 選取合適的δ值,計算每個量測點Xi到擬合平面的距離di,若判別式(12)成立,則判該點為正確值,反之,則判定為野值;
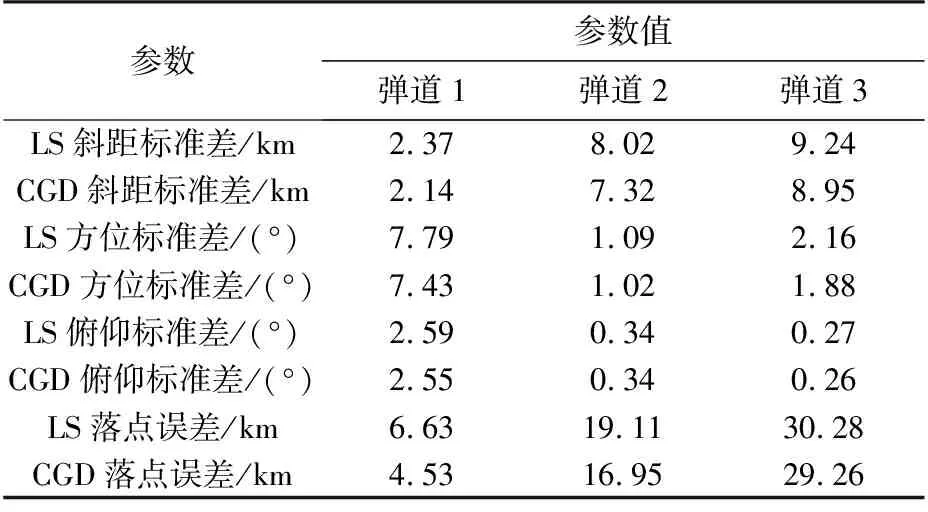
4) 由所有判定為正確值的量測點組成新的量測點集Xm(m≤n),令X=Xm,如果m 6) 對X′,在X,Y,Z三個方向上,分別對時間t作二項式最小二乘法擬合。 研究表明,通常情況下,數值法彈道外推的精度要高于解析法。得到地心慣性坐標系下的理論彈道后,轉換到地心地固坐標系,取彈道數據的中點作為彈道外推的初始點,建立彈道導彈動力學方程,采用數值法進行彈道外推。 本文采用STK軟件[13-14],仿真了3條標準彈道,分別為近、中、遠程導彈,發射時刻均為2018年1月1日0時0分0秒,彈道生成函數為Ballistic,發射地點為同一地點,其他參數如表1所示。 表1 STK模擬導彈參數 雷達站址緯度為33.843°,經度為136.452°,高度為500 m,數據率為1 Hz。雷達測量誤差滿足高斯分布,測量精度為:距離標準差為100 m,方位角標準差為0.12°,俯仰角標準差為0.12°。試驗中,對每組理論彈道進行了100次加噪模擬計算,取100次計算的平均值為最終結果。計算中,分別采用最小二乘法(LS)和基于幾何距離準則(CGD)的彈道外推方法進行外推,取中點為初始點。 在量測數據點數分別為50, 100和150的情況下,外推彈道和理論彈道在斜距、方位、俯仰三個緯度上的100次模擬的平均標準差和落點誤差分別如表2~表4所示。 表2 50個測量點情況下的試驗結果 表3 100個測量點情況下的試驗結果 表4 150個測量點情況下的試驗結果 從表2~表4中的數據可以看出,對于3種彈道,在量測數據點數分別為50,100和150的情況下,基于幾何距離準則的彈道外推方法的外推精度相比傳統的最小二乘擬合方法均有所提高,其中,用50組量測數據進行外推時,3種彈道在斜距、方位、俯仰三個緯度上的標準差平均減小2.38%,56.98%和3.03%,落點誤差平均減小29.03%;用100組量測數據進行外推時,3個維度的標準差平均減小5.07%,48.82%和0.31%,落點誤差平均減小20.08%;用150組量測數據進行外推時,3個維度的標準差平均減小7.19%,8.00%和1.75%,落點誤差平均減小15.45%。對比發現,基于幾何距離準則的彈道外推方法可以極大提高落點和方位角的預測精度,斜距和俯仰角預測精度提高不明顯。這一結果與上文中的算法原理符合。因為在3次仿真試驗中,導彈均朝著同一個方向發射,彈道平面基本重合,而雷達正好位于彈道平面內,量測誤差表現為對彈道平面的偏離。基于幾何距離準則的彈道外推方法首先擬合彈道平面,將偏離彈道平面的量測映射到平面內,因此可以極大提高方位角的外推精度,而斜距和俯仰角的誤差表現為平面內的偏移,該方法對二者外推精度的提高有限。可以預計,雷達量測初始值偏離彈道平面越大,該方法對彈道外推精度的提高越明顯。 另一方面,仿真試驗中,無論是初始量測數據點數為50,100或150,射程為1 000 km和4 000 km的導彈(彈道1和2)外推精度提高的百分比均大于射程為7 000 km的導彈。導致這一結果的原因是,隨著導彈射程的增長,導彈飛行時間隨之增長,彈道也會隨之逐漸偏離同一個平面;同時,現有的彈道外推的數值法都是基于理想的導彈動力學方程,當外推時間增長時誤差也不可避免地增大。因此,對于遠程導彈,基于幾何距離準則的彈道外推方法精度提高不大,但是,對于近、中程導彈,該方法外推精度的提高還是十分明顯的。 總的來說,對于近、中程導彈,基于幾何距離準則的彈道外推方法可以極大提高彈道外推的精度,對于遠程導彈,外推精度也有所提高,但提高幅度較小。特別是在偏離彈道平面的方向,該方法精度提高尤為顯著。 本文在充分研究彈道導彈軌道特性的基礎上,設計并實現了一種基于三維空間幾何距離準則的彈道外推方法。該方法首先在地球慣性坐標系中,確定彈道導彈軌道橢圓所在的平面,使所有量測點到該平面的幾何距離平方和最小,然后用各量測點在平面內的投影點代替原始點跡進行最小二乘法平滑,取其中點為初始點進行彈道外推。應用STK軟件進行彈道模擬仿真,分別使用傳統的最小二乘法和基于幾何距離準則的方法進行彈道外推,100次仿真試驗結果表明,無論是從雷達量測斜距、方位和俯仰標準差還是預測落點誤差進行比較,該方法的外推精度都有所提高,特別是對于近、中程導彈,外推精度提高很大。特別是在偏離彈道平面的方向,該方法精度提高尤為顯著。 該方法的核心在于充分利用彈道導彈的特性,從整體上確定彈道平面。如果將該方法與濾波結合起來,也許可以進一步提高彈道外推的精度。此外,該方法也可以應用到空間目標的軌道外推上。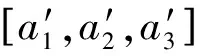
1.2 彈道外推
2 仿真結果
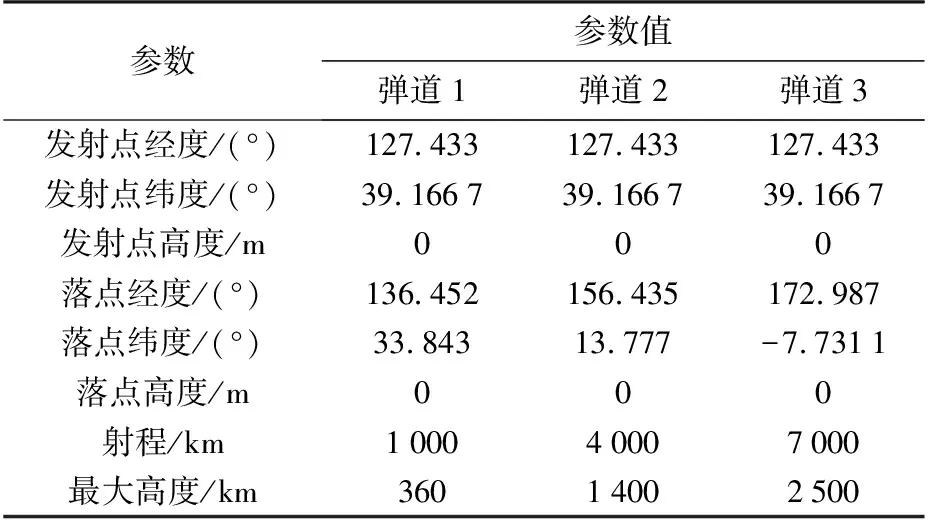
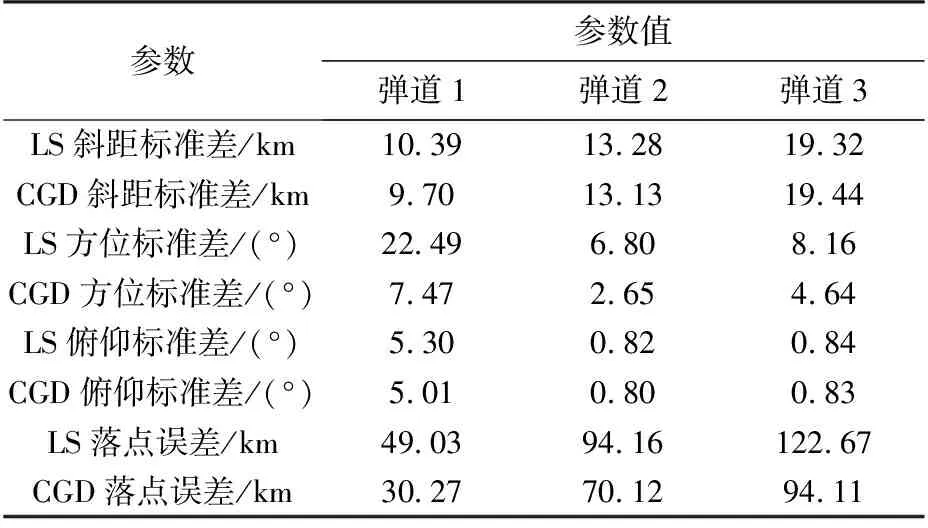
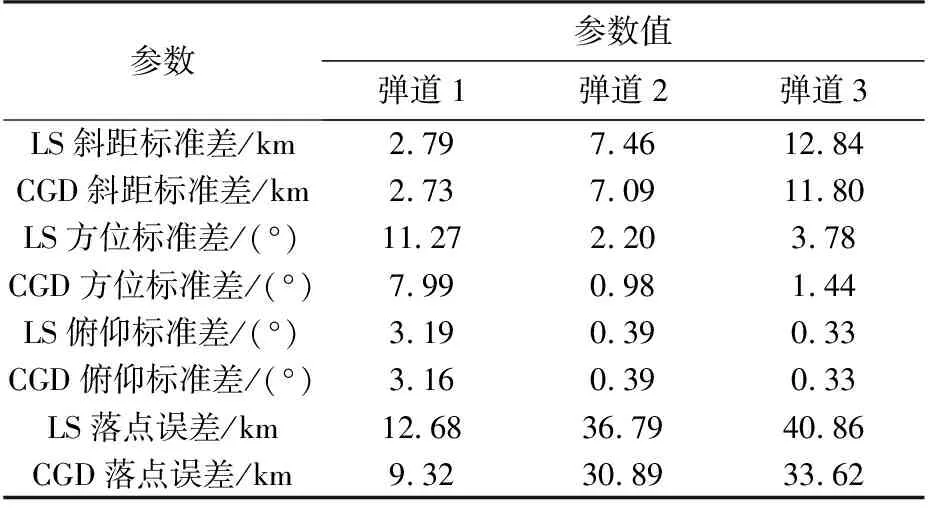
3 結束語

