表面織構動壓滑動軸承界面滑移研究*

(1.河南科技大學機電工程學院 河南洛陽 471003;2.洛陽鐵路信息工程學校 河南洛陽 471000；3.洛陽LYC軸承有限公司 河南洛陽 471000)

傳統流體力學與摩擦學普遍認為流體黏在流-固結合處，流體運動的速度和固體運動速度相同，即兩者之間不存在界面滑移現象。隨著近些年的研究深入，流-固之間的界面滑移現象越來越受到國內外學者的關注。1984年，CHURAEV等[1]進行水與水銀流動實驗時發現了界面滑移現象。ZHU和GRAUICK[2]在云母表面形成的流體膜中發現了界面滑移現象。CHO等[3]研究發現，界面滑移的距離同流體的黏性、接觸角以及極性等因素有關。陳暉和沈明[4]研究發現，固體表面的親/疏液性會導致界面滑移現象的發生，界面滑移速度受疏液型壁面的影響較小。OU等[5]研究發現，通過改變親疏水性結構后，界面滑移之間的摩擦力降低了40%。高誠輝等[6]研究發現，流體黏度的大小影響著固-液界面間滑移現象的產生。SPIKES[7-8]研究發現，界面滑移剪切力等于0時，軸承界面滑移的承載力僅為無界面滑移的1/2，且摩擦力降低了若干個數量級。

表面織構是一種提高承載和降低磨損的有效手段，已得到眾多學者的廣泛關注[9-11]。“人工表面織構”這一概念由HAMILTON等[12]提出，并通過試驗驗證“人工表面織構”能夠改善摩擦副之間的摩擦學特性。ETSION[13]研究表明，部分表面織構能夠在減摩方面起到更好的作用，通過加工部分表面織構的活塞環，使內燃機能耗降低了40%。

表面織構因具有減摩和潤滑作用[14]，在軸承上得到了廣泛應用。TALA-IGHIL等[15-16]分析了表面織構位置與軸承摩擦學性能的關系，驗證了表面織構可以增加油膜厚度，減小軸承的摩擦。

以上研究表明，表面織構與界面滑移會對軸承的摩擦學性能產生影響。然而，目前界面滑移和表面織構摩擦力二者之間的關系缺乏一個詳細而又具體的描述，且二者共同作用下動壓軸承摩擦學性能的有關理論與數學模型研究缺乏。本文作者結合力學平衡方程和流體力學方程，推導了產生界面滑移的油膜速度與剪切應力的函數；結合表面織構楔形油膜模型得到摩擦力表達式，通過建立其有限元模型，探究了表面織構動壓軸承界面滑移規律，并闡述其產生機制。

1 界面滑移理論模型

1.1 油膜表面剪切力模型

假設：油液是牛頓流體且不可壓縮；油液為層流，不考慮重力、慣性力以及壓力引起的油液黏度變化；油膜壓力在厚度方向不發生任何變化。建立動壓軸承簡化模型如圖1所示，動壓滑動軸承油膜壓力示意圖如圖2所示。

任取圖1所示油液中一個微元體，如圖3所示。根據二力平衡公理，則：

(1)

經過化簡和整理：

(2)

根據牛頓流體模型，則黏滯剪切力如下：

(3)

對式(3)求導，聯立式(2)經整理后：

(4)

對經整理后的式(4)進行二次積分，則：

(5)

其中，C1和C2是待定常數。聯立式(5)和式(2)，則剪切力為

(6)

文中以τ1和τ2分別表示油膜上表面和下表面的剪切力。

圖1 動壓軸承簡化模型

圖2 動壓滑動軸承油膜壓力示意圖

圖3 微元體受力平衡示意圖

1.2 無界面滑移的油膜剪切力

無界面滑移時的邊界條件如下，令h表示油膜厚度，則：

(7)

聯立式(5)和式(7)，可得到油液速度分布函數表達式如下：

(8)

由式(8)可知，油液速度u包括2部分：一部分是以油液方向z為自變量的線性單調函數；一部分是非線性函數，呈拋物線狀，表示油液在x方向壓力變化導致的速度變化。界面滑移的產生不僅可以在收斂區域(升壓區)，還可以在發散區域(降壓區)。油液速度出現凹形和凸形變化規律主要由?p/?x所引起的。位于收斂區域內時，則?p/?x>0，那么油液速度分布呈現出非線性的凹形曲線變化；當?p/?x=0時，此時油液速度分布呈現一種線性變化；位于發散區域內時，則?p/?x<0，那么油液速度分布呈現出非線性的凸形曲線變化。無界面滑移油液xOz坐標系下的速度分布，如圖4所示。

結合式(8)和式(6)，油膜剪切力τ表達式如下：

(9)

此時，油膜剪切力τ1和τ2表達式為

(10)

油膜剪切力中ηv1/h表示正值，當?p/?x>0時，h值越大，τ值越大；油液由發散區域(降壓區)向收斂區域(升壓區)流動時，τmax產生于油液的上表面處。故，軸徑同油液接觸層率先引起界面滑移。當?p/?x<0時，h值越大，τ值越小；當油液由收斂區域向發散區域流動時，τmax產生于油液的下表面處。故，軸承同油液接觸層率先引起界面滑移。當?p/?x=0時，τ值表示定值；當且僅當|τ1|=|τ2|=τ0(τ0表示界面滑移時的油膜剪切力)時，軸承與軸徑同油液接觸層同時產生界面滑移現象。無界面滑移油液xOz坐標下剪切力分布，如圖5所示。

圖5 無界面滑移油液xOz坐標系下的剪切力分布

1.3 油液上表面滑移的剪切力

油液上表面產生界面滑移時，?p/?x>0，u1≠v1但是u2=v2=0。此時，存在一個速度差Δu1=v1-u1。定義軸承產生界面滑移時的滑移比：

(11)

則滑移比k1≥0。在此情形下油液的邊界條件如下：

(12)

聯立式(12)和式(5)，得到油液速度分布函數表達式如下：

(13)

因為?p/?x>0，由式(13)可知，界面滑移只能產生在收斂區域(升壓區)。故，油液速度分布呈現出非線性的凹形曲線變化，如圖6所示。

圖6 上表面滑移油液xOz坐標系下的速度分布

則油液產生界面滑移時的剪切力表達式為

(14)

根據式(14)，產生滑移油液xOz坐標系下的剪切力分布如圖7所示。此時，明顯τmax產生于油液的上表面處。

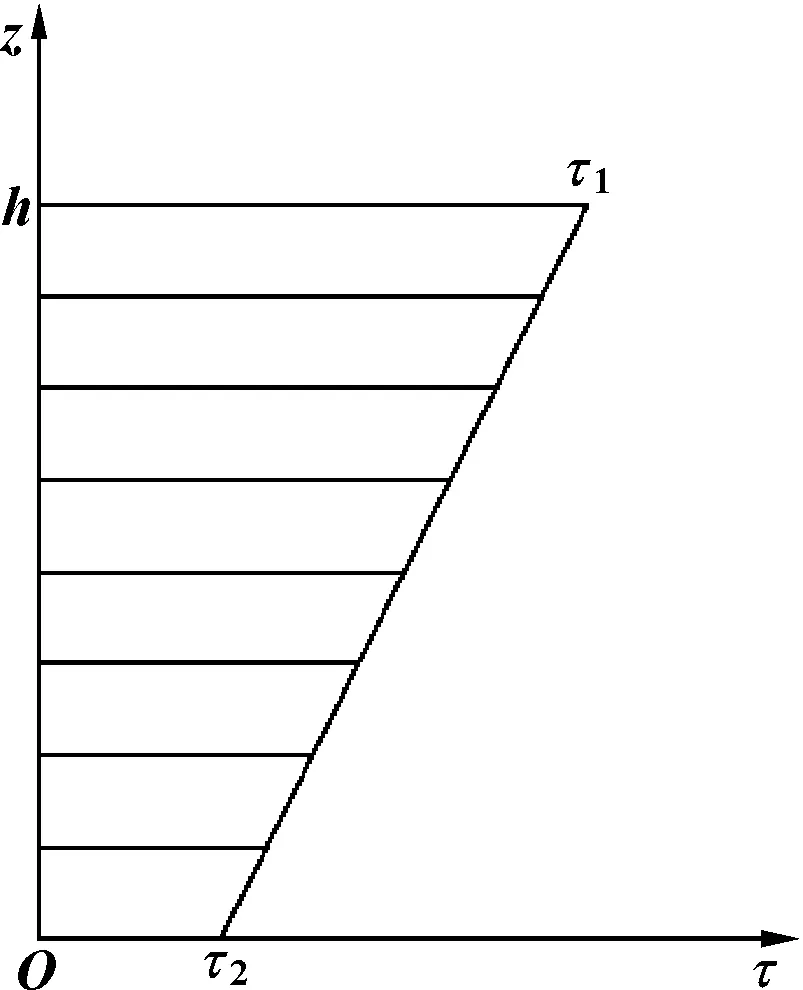
圖7 上表面滑移油液xOz坐標系下的剪切力分布

1.4 油液下表面滑移的剪切力

油液下表面產生界面滑移時，?p/?x<0，u1=v1但是u2≠v2且u2=0。此時，存在一個速度差Δu2=v2-u2。定義軸承產生界面滑移時的滑移比：

(15)

則滑移比k2≤0。在此情形下油液的邊界條件如下：

(16)

聯立式(16)和式(5)，得到油液速度分布函數表達式如下：

(17)

因為?p/?x<0，由式(17)可知，界面滑移只能產生在發散區域(降壓區)。故，油液速度分布呈現出非線性的凸形曲線變化，如圖8所示。

圖8 下表面滑移油液xOz坐標系下的速度分布

則油液產生界面滑移時的剪切力表達式為

(18)

根據式(18)，產生滑移油液xOz坐標系下的剪切力分布如圖9所示。此時，明顯τmax產生于油液的下表面處。

圖9 下表面滑移油液xOz坐標下的剪切力分布

1.5 油液上/下表面同時滑移的剪切力

上/下表面均產生界面滑移時，|τ1|=|τ2|，此時u1≠v1，u2≠v2。存在的速度差分別是Δu1=v1-u1和Δu2=v2-u2。定義產生界面滑移時的滑移比：

(19)

其中，0≤k1≤1。油液的邊界條件如下：

(20)

聯立式(19)和式(5)，得到油液速度分布函數表達式如下：

(21)

則油液兩表面產生界面滑移時的剪切力表達式為

(22)

油液剪切力|τ1|=|τ2|存在2種可能性，下面分別予以討論。

(1)當τ1=τ2時，由式(22)可得：

(23)

式(23)表明，在油液上/下表面同時發生滑移的情況下，界面滑移發生于油液壓力極值點位置處。

聯立式(23)和式(21)，可得：

(24)

上/下表面均滑移時油液的速度與剪切力分布，如圖10所示。

然而，當?p/?x=0時，此種狀況可以不予考慮，原因在于存在承載力和摩擦力在軸承中起到的作用有限。因此，下文中對此不再贅述。

圖10 上/下表面均滑移時油液的速度和剪切力分布 (τ1=τ2)

(2)當τ1=-τ2時，由式(22)可得：

(25)

收斂區域(升壓區)和發散區域(降壓區)油液xOz坐標系下速度和剪切力分布，如圖11所示。

圖11 上/下表面滑移xOz坐標下速度和剪切力分布(τ1=τ2)

2 表面織構動壓軸承摩擦力計算模型

2.1 表面織構動壓滑動軸承模型建立

楔形油膜模型作為動壓滑動軸承的簡化模型，常常被認為是研究動壓軸承的基礎。選擇表面織構的楔形油膜模型進行研究，該模型的入口油液厚度、出口油液厚度以及長度分別是h1、h2和g。如圖12所示，將不同位置的表面織構按順序命名1#，2#和3#，其底邊長和深度分別為d1、d2、d3以及h3、h4、h5。

圖12 表面織構楔形油膜模型示意圖

為方便對比表面織構摩擦力的變化，選擇無織構無滑移的軸承摩擦力作為基準。定義相對摩擦力為表面織構軸承摩擦力同基準二者之比。為了描述表面織構油膜厚度在不同位置處的變化，因變量油膜厚度h是一個關于自變量x的線性函數：將坐標點a、b、c、d、e、f的左右兩邊，分別用a+、a-，b+、b-，c+、c-，d+、d-，e+、e-，f+、f-表示。因此，表面織構油膜厚度h表達式如下：

(26)

表面織構楔形油液模型摩擦力公式為

(27)

聯立式(26)與(27)，則表面織構軸承不同界面滑移下的摩擦力為

(28)

式中：p1、p2表示沿x軸在0與g位置的壓力。

由式(28)可知，表面織構摩擦力包括3部分：第一部分是由滑移比與軸頸速度二者共同決定的同油液速度相關的摩擦力，其值大小與壓力無關；第二部分為同進/出口壓力相關的摩擦力，其值大小同進/出口油液壓力以及油液厚度大小相關；第三部分的

2.2 數值模擬與分析

為了避免其他因素對摩擦力的干擾，分別建立3種不同的單一織構分布模型，詳細的結構參數如表1所示，即建立的模型分別將織構分布于1/6、1/2與5/6的長度位置上。

表1 表面織構結構參數

對不同位置的表面織構軸承進行有限元模擬分析，研究織構在不同位置下的界面滑移情況。有限元模擬時有關參數的設置，如表2所示。

表2 數值模擬參數設置

動壓滑動軸承界面滑移比與相對摩擦力關系如圖13所示。

由圖13(a)可知：當油液上表面發生界面滑移時，其相對摩擦力與界面滑移比的關系同光滑軸承變化趨勢相同，表現線性分布變化，且發生界面滑移的油液上表面相對摩擦力隨界面滑移比的增加而逐漸減小。油液上表面界面滑移比的增加，使得油液速度變慢，進而引起油液速度變化率減小。由式(3)可知油液剪切力同速度變化率成正比，因此隨界面滑移比增加而相對摩擦力減小。由式(28)可知，摩擦力對不同參數的敏感程度是不同的，對速度比較敏感，但對載荷和油膜壓力的變化比較遲鈍。

由圖13(b)可知：當油液下表面發生界面滑移時，其相對摩擦力與界面滑移比也呈現線性關系，且滑移比越大摩擦力越小；此時表面織構軸承的下表面界面滑移速度對相對摩擦力影響起主要作用。表面織構軸承界面滑移速度越大，減摩作用越佳。圖13(a)、(b)所示的4種模型中，摩擦力表現最佳的是模型3，該模型的摩擦力最小。

圖13 不同界面滑移的相對摩擦力與滑移比關系

由圖13(c)、(d)可知：上/下表面界面均滑移時不同模型的相對摩擦力變化趨勢基本一致；滑移比k≤0.5時，相對摩擦力隨界面滑移比基本呈線性變化，且滑移比越大，相對摩擦力越小；滑移比k≥0.5時，相對摩擦力隨著滑移比增加而逐漸增加。4種模型中，表面織構模型的摩擦力相比光滑模型均明顯減小。可見，表面織構具有優異的減摩作用，其中模型3的減摩效果最佳。

滑移比k=0.4時不同界面滑移的油膜表面壓力分布如圖14所示。由圖14(a)可見：織構布置在出口附近時，引起的動壓作用最明顯，而布置在入口附近時，對周邊的動壓作用不明顯；模型1和2的油膜壓力與摩擦力略高于光滑模型，模型3的油膜壓力同無織構近似一致，但摩擦力最小，表明合適的織構分布在減摩和承載方面能夠起到較好的作用。由圖14(b)可見：模型的動壓效應受到織構的影響且周圍的油膜壓力產生明顯波動，此時，高于圖14(a)中發生界面滑移時的油膜壓力。

由圖14(c)、(d)可見：不同模型上/下界面均滑移時，織構模型動壓效應比較突出，織構的存在形成的油膜壓力峰值均高于光滑模型的油膜壓力峰值；織構模型的周圍油膜壓力出現顯著的變化。位于減壓區的織構模型3，油膜壓力相較光滑模型提高了30.9%，而摩擦力僅為光滑模型的22.4%(如圖13(d)所示)，展示出優良的減摩和承載性能。因此，恰當的織構排布不僅能提高油膜壓力，還可以降低摩擦。

圖14 不同界面滑移的油膜表面壓力分布(k=0.4)

綜上，承載和減摩最佳的織構位置分布為模型3。圖15示出了模型3界面滑移下的速度云圖。

文中選擇滑移比k=0.4且發生界面滑移的有限元模擬速度云圖如圖15(a)、(b)所示。由圖15(a)、(b)可看出：發生界面滑移的上表面速度受到表面織構影響不大，原因是存貯在織構中的潤滑油依然保持靜止；但是發生界面滑移的下表面對周圍油液速度的影響卻變大，然而存貯在織構中的潤滑油仍然未能充分流動，油膜表面的速度場也未發生明顯的變化，表明軸承速度仍然是影響模型表面界面滑移的主要因素。

比較圖15(c)、(d)與圖15(a)、(b)可知，織構的存在對其周圍的油液速度產生了較為明顯的影響。因為織構的存在增大了油膜厚度，引起油液周圍的平均速度減小，使得發生向下凹陷的速度曲線，油液表面速度變化率減小，造成油液剪切力減小，進而起到減摩的作用。

3 結論

(1)油膜發生界面滑移時，在升壓區和降壓區油膜速度分別表現為非線性的凹形和凸形變化規律；油膜在上表面和下表面發生滑移時的最大剪切力分別位于油膜上表面和下表面處；而上/下表面均滑移時的最大剪切應力位于上/下表面且二者相同。

(2)油膜界面滑移狀態的表面織構動壓滑動軸承的摩擦力受到織構位置分布的影響，分布在中部與入口處的表面織構減摩與承載性能不如分布在出口處的表面織構；上/下表面均發生界面滑移時，位于出口處的表面織構呈現出優異的減摩與承載作用，且摩擦力約為無滑移時的4%～17%。

(3)不同模型的界面滑移摩擦力隨滑移比增大而減小；排布不同的表面織構模型呈現了不同的承載和減摩性能，模型3在不同滑移下的摩擦力最小，而油膜壓力同無織構近似一致，該模型的織構分布在減摩和承載方面能夠起到較好的作用。

(4)表面織構軸承界面滑移產生的機制主要是潤滑油具有牛頓流體的黏滯特性。文中表面織構軸承的作用規律和界面滑移機制的研究，對動壓滑動軸承的減摩和優化設計奠定了理論基礎。