基于結構方程與蒙特卡洛方法的鉆井現場作業風險評價

趙春蘭 殷慧敏 王 兵 范翔宇 吳 昊

1.西南石油大學理學院 2.西南石油大學計算機科學學院3.“油氣藏地質及開發工程”國家重點實驗室·西南石油大學 4.中國石油西南油氣田公司勘探事業部

0 引言

油氣鉆井作業是一個隱蔽性強、有較大的不確定性和高風險的系統工程[1]。隨著油氣勘探開發的不斷發展[2]，鉆井作業變得日益頻繁，鉆井條件和地質條件也越來越復雜，致使鉆井作業處于危險的境地，鉆井事故也就時有發生[3]。

目前，對于鉆井風險的評估方法已有相當多的學者進行研究[4-8]。李環等[4]基于HAZOP定性分析法評估鉆井作業風險的大小。李海宏[5]通過層次分析法建立多因素多層次鉆井風險定量評價模型，定量分析法因其考慮鉆井作業數據來分析問題得以廣泛應用。上述都是常規確定性方法，并未考慮評價數據的不確定性，因此，提出了一些不確定性分析方法來解決這些問題。金業權等[6]提出了基于三角模糊數的鉆井井控風險定量評價模型；李琪等[3]采用AHP與模糊綜合評價相結合的方法建立了鉆井風險綜合評價模型；以及確定指標權重結合模糊綜合評價法評估鉆井風險等級的其他方法。因子與指標間的關系存在主觀干擾，使得結果出現誤差，最終可能導致所確定的權重與實際不符，而常規的權重計算法無法確定各因子之間的直接或間接關系。結構方程模型（SEM）不僅可以很好地解決這個問題[7]，并且可找到關鍵風險因子。錢志雷等[7]利用SEM構建了石油企業國際石油工程項目的風險評價方法。

但SEM的數據收集困難，其數據往往要求服從正態分布，為了得到更方便的數據樣本，基于現場數據各因子的分布特征，借助蒙特卡洛方法（MC）生成一系列服從正態分布的風險因子樣本數據。同時由于模糊綜合評價法是以專家打分的方式得到評判結果缺乏一定的客觀性，而MC是一種利用隨機數來解決問題的技術，不但考慮了風險因素變動的幅度，還考慮了這種變動幅度發生的可能性大小及對考察指標的影響程度，使得評價結果更加客觀合理。

為了更好地處理數據結構中的不確定性問題，找到關鍵因子和指標之間的關系，進而得到客觀的評價結果，筆者結合上述兩種方法建立以危險度（R）來衡量風險程度的SEM—MC新模型，并應用于四川盆地某油氣田現場。

1 方法原理

1.1 結構方程模型

SEM是一種基于變量協方差矩陣來分析變量之間關系的多元統計分析方法學[9-11]。它把因子分析與路徑分析相結合，對于一些不能直接測量的研究變量用可觀測的變量作為潛在變量（以下簡稱潛變量）的“標志”，利用因子分析的方法將觀測變量與潛變量聯系起來，結合路徑分析找到潛變量之間的結構關系[12]。

SEM分為測量模型和結構模型兩部分，如圖1所示。

測量模型主要用來描述外源（內生）觀測變量與外源（內生）潛變量之間的關系，由兩個典型的因子模型組成，即

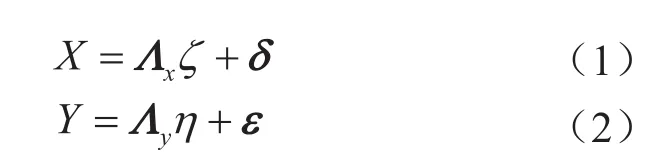
結構模型主要是描述潛變量之間的關系，包括外源潛變量對內生潛變量的影響，以及內生潛變量之間的影響，是一種因果模型[12-13]，即

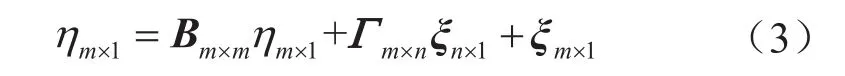
式中δ表示外源觀測變量X的測量誤差向量；ε表示內生觀測變量Y的測量誤差向量；Λx表示外源觀測變量關于外源潛變量的負載矩陣；Λy表示內生觀測變量關于內生潛變量的負載矩陣；Гm×n表示外源潛變量對內生潛變量的影響系數矩陣；Bm×m表示內生潛變量之間的影響系數矩陣；ξ表示結構誤差向量[9,12-13]。

式（1）規定了外源潛變量（ζ）和外源觀測變量（X）之間的聯系，式（2）規定了內生潛變量（η）和內生觀測變量（Y）之間的關系，式（3）規定了外源潛變量與內生潛變量、內生潛變量與自身之間的關系。

1.2 蒙特卡洛方法

MC屬于試驗數學的一個分支，它利用隨機數進行統計試驗，能夠隨機模擬各變量間的動態關系[14]，得到大量模擬測量結果并分析，進而解決某些復雜的不確定性或風險性問題。

筆者基本研究思路如下：

假設隨機變量X的數學期望E（X）是需要計算的變量，X1, X2, …, XN是一系列隨機數重復采樣N次得到的。本系列的平均值計算如下[15]：

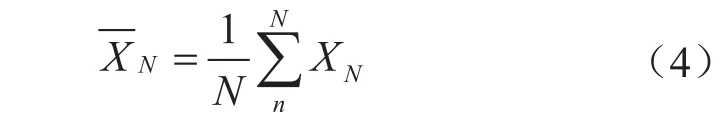
根據大數定律，當N的采樣次數足夠多時，即為

通過使用MC方法來評估鉆井風險等級，可以根據每個變量的分布生成一系列樣本數據，確定事故后果與風險因素之間的關系。

對于多維隨機變量的MC模擬問題，往往假定各隨機變量是相互獨立的，而在某些實際應用中，多維隨機變量卻具有一定的相關性。一般多維相關正態分布隨機變量序列可以通過協方差矩陣的Cholesky因子對獨立正態分布隨機變量序列進行線性變換來產生[16]。基于研究目的，筆者運用SEM中得到的變量間的線性模型來求得事故后果與各風險因素關系進行MC模擬，并利用@Risk7.5軟件來執行。

1.3 SEM—MC新評估模型的構建

對于相同的危險度數值，一般模型只考慮了其事故后果分值與事故可能性指標分值的簡單累積，這不能真實反映客觀風險水平[17]。為此，筆者提出了SEM—MC的鉆井風險新評估模型。

針對鉆井現場作業風險因素具有的不確定性，首先構建鉆井現場作業風險因子，利用SEM求出各風險因子的相關性，并求得指標權重確定關鍵風險因子，再由各因子的數據分布特征，利用MC進行模擬，求得潛變量的模擬值，結合事故后果值及其指標權重建立SEM—MC的鉆井風險新評估模型（圖2）。

其構思的3個步驟：①通過收集鉆井風險數據，刪除不顯著因子，確定風險指標體系；②結合SEM求得風險因子權重，以識別影響鉆井現場作業安全的關鍵風險因子，同時利用風險后果權重以確定事故后果的程度；③根據風險因子的數據特征結合步驟2的測量模型，利用MC模擬出潛變量的模擬值（即事故可能性因素分值）；④最后利用MC模擬事故可能性因素分值與事故后果嚴重程度累積的風險評估新模型，即

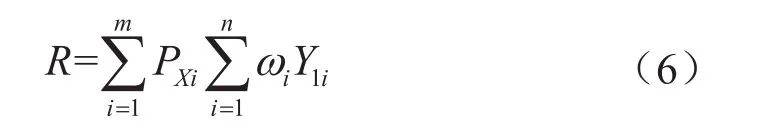
式中R表示危險度；PXi表示事故可能性因素分值，ωi表示事故后果影響權重；Y1i表示事故后果分值；ωiY1i表示事故后果程度。

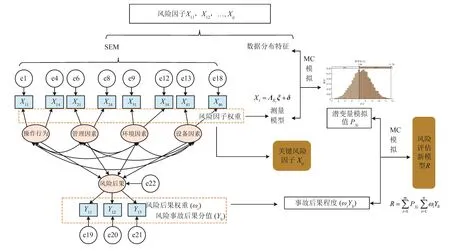
圖2 SEM—MC風險評估新模型構思圖

2 鉆井作業風險評價指標的確定

2.1 數據收集

油氣鉆井作業的風險指標體系具有復雜性、多層次的特點[7]，其現場作業風險因素較多，通過收集現場數據、咨詢鉆井作業專家并結合因子分析[18]，確定操作行為、管理因素等4個方面的因素，違章作業、生產管理缺陷等18個鉆井作業風險指標以及涉及人員、設備事故[19-21]和環境污染這3種事故后果。對四川盆地某油氣田鉆井現場數據進行收集，主要收集2011年365 天內各風險指標每天發生的次數以及所造成事故的情況。各指標部分數據如表1所示。

2.2 數據處理

2.2.1 異常值處理

異常值是指樣本中的個別數值明顯偏離其所屬樣本的其他觀測值，因其會對結果造成一定的影響。筆者利用iForest算法對數據進行異常值處理，尋找出與大部分數據不一樣的異常數據，將其中與研究規律不符合，干擾結果的數據從中剔除，最后共剔除包含日期（月/日）為3/23、3/26、4/5、4/12等19個異常樣本值。

2.2.2 數據的正態性檢驗

考慮到結構方程模型一般是問卷調查獲得的數據，且要求數據服從正態分布。基于本文所用的是真實觀測數據，無法直接進行AMOS分析。因此需要先進行正態性檢驗和等級變換分析。

通過累積頻率來了解各個指標值的分布情況，首先利用Matlab軟件計算2011年各個指標的頻率，先將數據通過快速排序方法進行排序，再按數組下標進行掃描，記錄頻數，最后計算得到如場所不符合要求（圖3-a）和井控設備缺陷（圖3-b）等指標的累積頻率。

2.2.3 等級程度的劃分

利用正態分布數據的特性，根據風險因子每天發生次數的頻率劃分等級，發生次數越少導致事故發生的可能性越小，反之越大。按正態分布函數，以置信區間概率 [0 20%）、[20% 40%）、[40% 60%）、[60%80%）、[80% 100%） 作為風險等級劃分的基本區間，分別記為安全，較安全，一般，較危險，很危險等5個等級程度，且按照1～5分進行打分，將每個風險因子導致事故的可能性分值記為PXij（Xij表示風險因子）。按照上述方法對風險指標進行處理，以作業場所不符合和井控設備缺陷為例（圖4），最后各風險指標導致事故的可能性分值部分數據如表2所示。

從圖4可以看出，井控設備缺陷的累積頻率在 0處接近10%，在10以上不到10%，由此說明大部分值處于（0, 10）。因正態分布與伽馬分布均具有這樣的特征，即圖3中指標與正態分布和伽馬分布的累積頻率圖像類似，所以鉆井風險的各指標值大致服從正態分布。

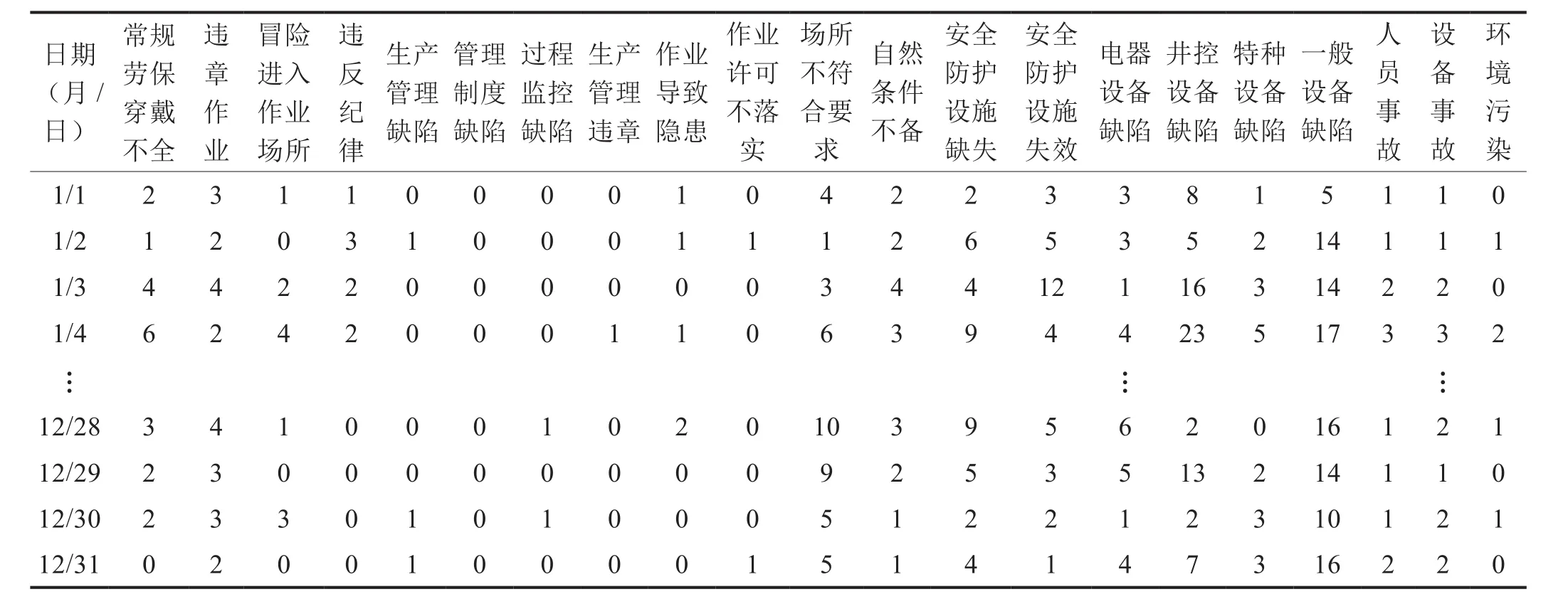
表1 四川盆地某油氣田鉆井現場作業2011年各風險指標及事故后果發生次數表

3 實例分析

3.1 模型的構建

3.1.1 鉆井現場作業風險結構方程模型的設定

根據鉆井現場作業風險的理論知識與相關經驗，操作行為、管理因素、環境因素和設備因素直接影響到鉆井作業的安全問題，同時這些因素之間也存在著一定的內在聯系，基于此構建如圖5所示的結構方程模型。

圖3 部分指標的頻率累積圖

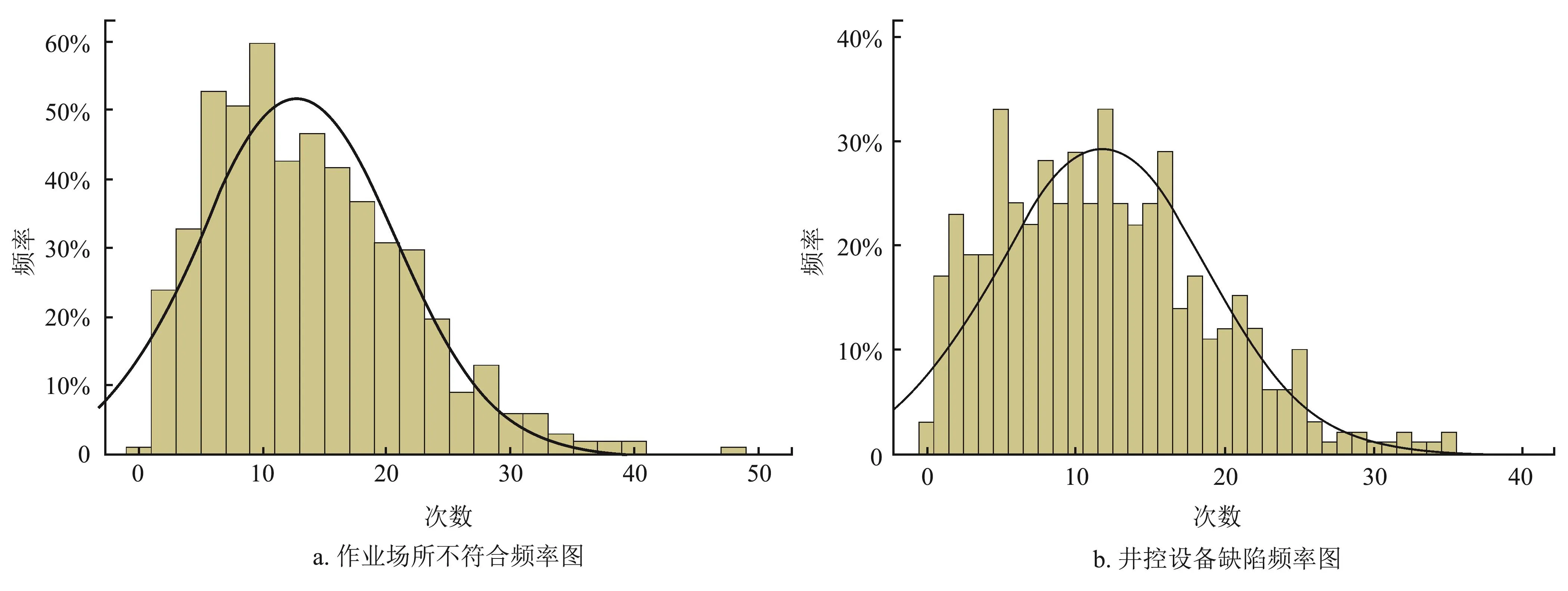
圖4 部分指標的正態分布頻率圖

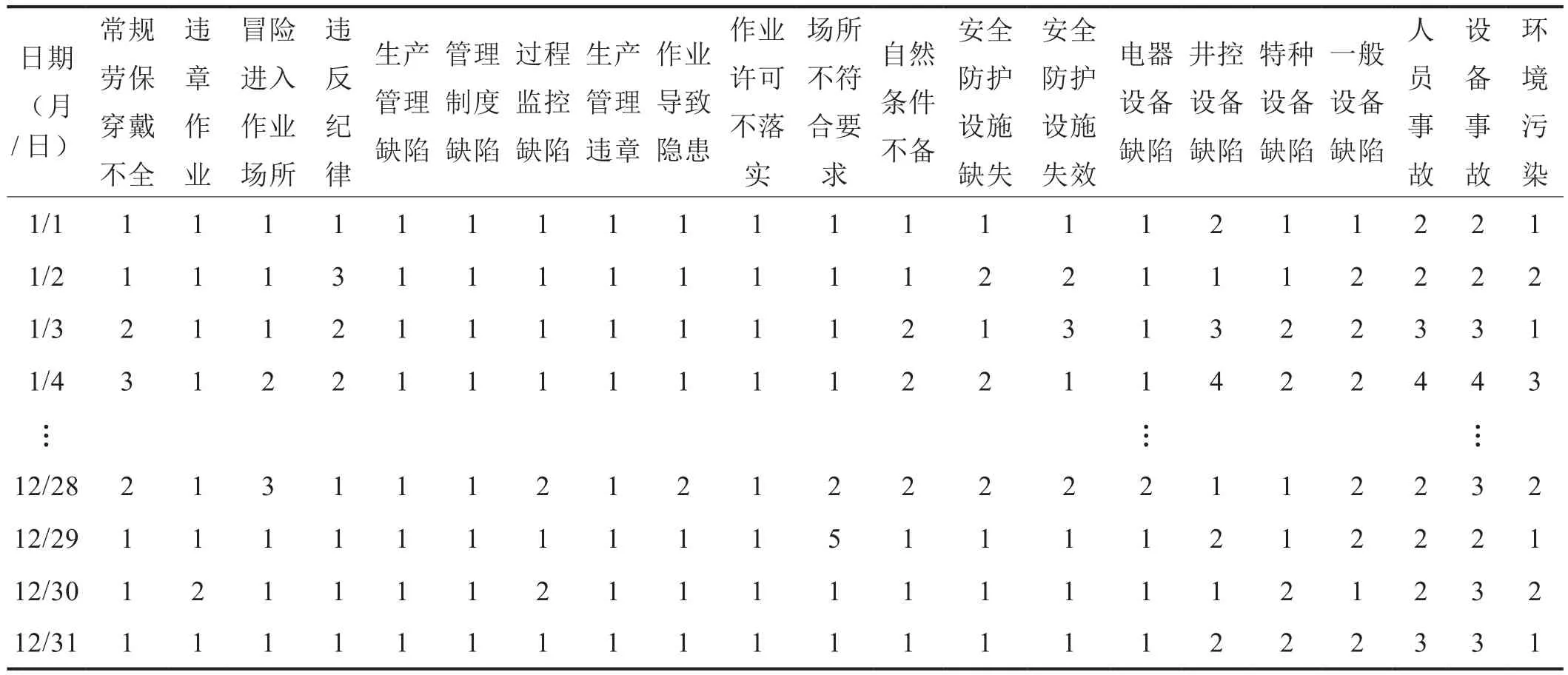
表2 四川盆地某油氣田鉆井現場作業2011年各指標導致事故的可能性及事故后果分值部分數據表

利用SPSS 20.0對處理后的數據進行因子分析，提取公因子并設定其為潛變量，分為作業人員的操作行為X1、管理層的管理因素X2以及環境因素X3、設備因素X4和鉆井風險Y，其下對應為各自的觀測變量，所以確立測量模型及結構模型如圖5所示。

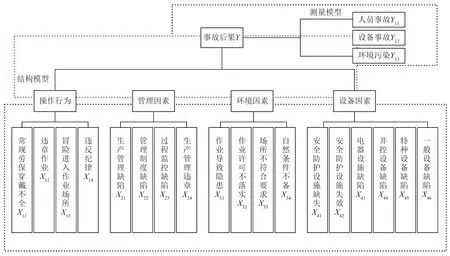
圖5 鉆井風險結構方程模型

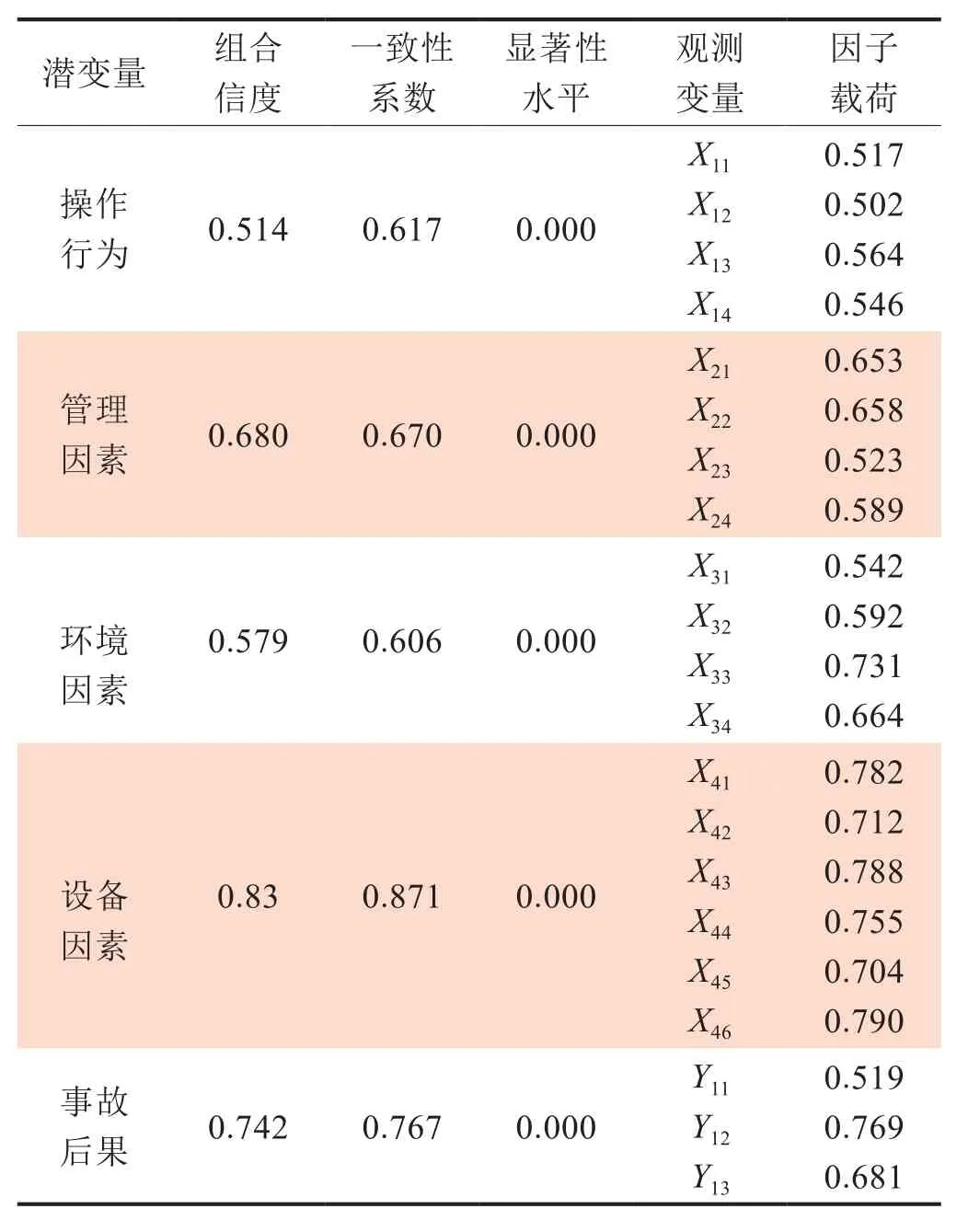
表3 信度與效度檢驗表

3.1.2 模型檢驗

測量模型主要根據可信度和效度進行判定，可信度的參數由潛變量的組合信度和一致性系數組成[22]，運用SPSS 20.0進行因子分析計算的結果如表3所示。由表3可知，所有潛變量的組合信度和一致性系數都大于0.5，顯著性檢驗指標為0.000明顯小于顯著性水平，表明了測量模型具有較好的可信度。同時，各觀測變量的因子載荷都接近0.5，說明潛變量的結構效度較好。

3.1.3 模型的擬合及評價

通過對模型進行反復的修正和擬合，依據AMOS軟件輸出的擬合指數進行判斷，建立的SEM的各項適配度指標檢驗結果如表4所示。檢驗結果顯示，模型的多項擬合指數均符合要求，擬合效果較好，模型是合理的，且修正后的模型比原模型擬合優度更高，故采納修正后的模型[23]。

將處理后的數據導入AMOS軟件中，得到標準化估計結果，如表5和圖6所示。

3.1.4 模型分析

由圖6和表5可知[23]，根據SEM結構模型得到可觀測潛變量因素之間關系，潛變量如操作行為、管理因素、環境因素、設備因素分別與鉆井事故后果的相關系數依次為0.32、0.50、0.31、0.42；而管理因素與設備因素的關系為0.93，與環境因素的關系為0.92，設備因素和環境因素關系為0.94。由此可見，管理因素對事故后果影響最大，其次是設備因素，環境因素影響最小。同樣，根據測量模型可得各風險因子間關系，風險因子如作業場所不符合與一般設備缺陷的關系0.57為最大，其次是場所不符合與安全防范設施缺失，電器設施缺陷關系為0.56，違章作業和管理制度缺陷關系0.06為最小。

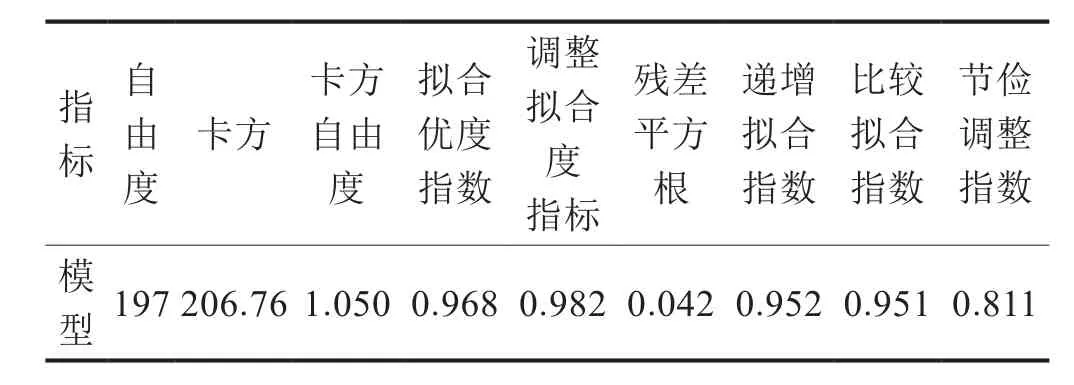
表4 SEM模型擬合效果檢驗表

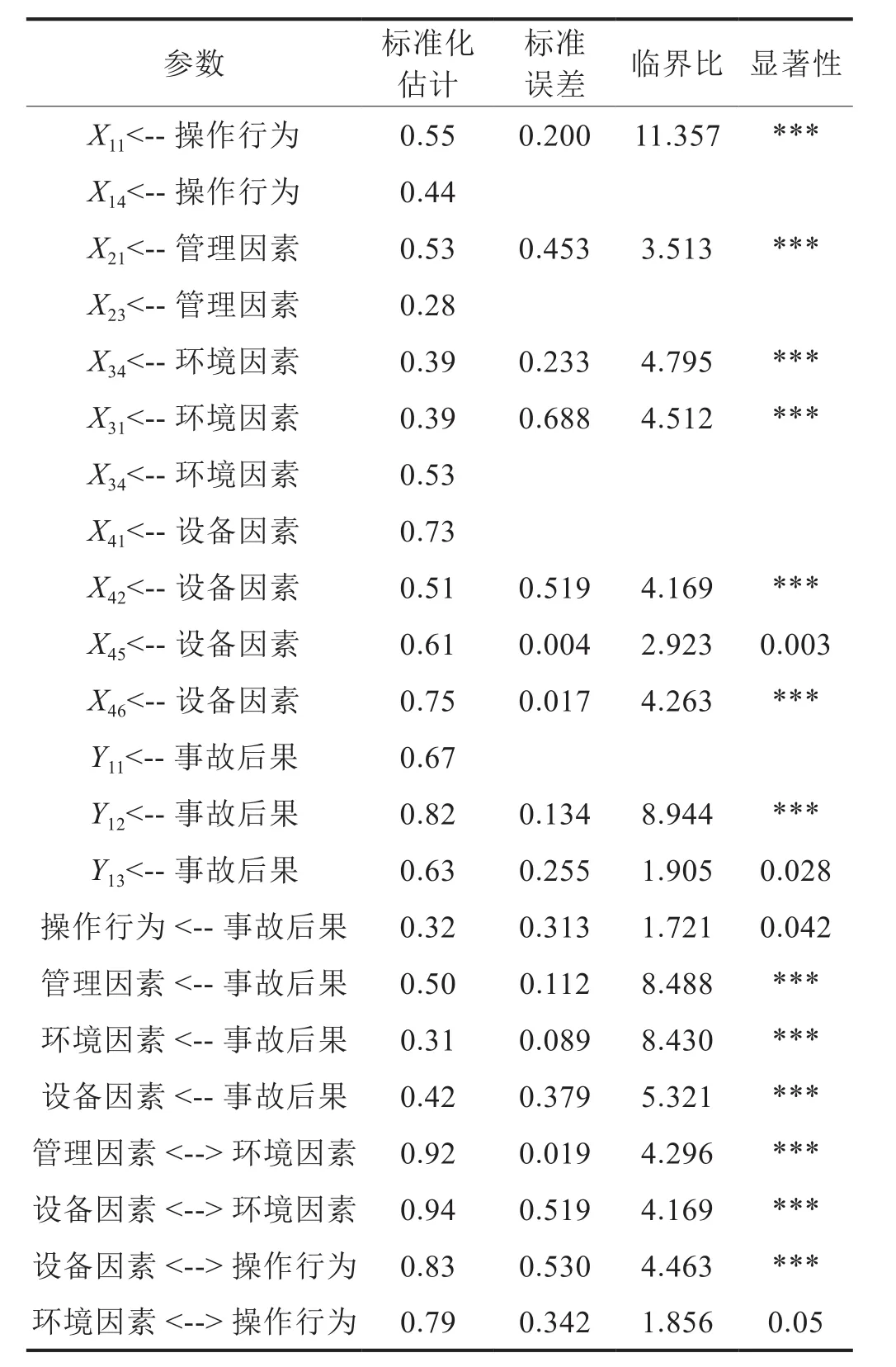
表5 部分參數估計及其檢驗表

圖6 鉆井現場作業風險模型標準化估計結果圖

根據路徑分析求得各風險因子的標準化系數作為權重大小，找到關鍵因子。潛變量在操作行為中的關鍵風險因子為常規勞保穿戴不齊（X13），管理因素的關鍵風險因子是生產管理缺陷（X21），環境因素中是作業場所不符合（X33），設備因素中是一般設備缺陷（X46）。

在結構方程模型中，由于內生潛變量事故后果受操作行為等4個外源潛變量的影響，以及人員事故等3個觀測潛變量的共同作用，且通過觀測潛變量來表現。

由式（1）～（3），可得

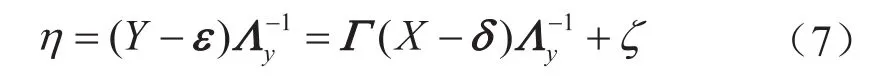
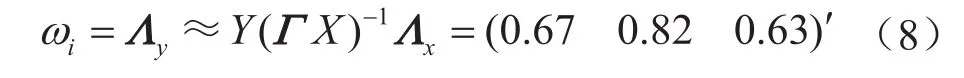
3.2 建立SEM—MC的鉆井現場作業風險評價

3.2.1 風險等級的確定[24]

由前面對本文數據的分析可知，基于結構方程模型的正態性檢驗，確定各風險因子的分布范圍及其峰值。利用MC隨機模擬程序對給定的各個因素區間內隨機地獲取5 000個數值[14]，根據表3確定的風險因子導致事故的可能性分值（PXij），通過SEM測量模型式（1）可以確定PXi（即外源潛變量的可能性分值），基于MC中對各風險因子的模擬數可得潛變量的模擬值變動范圍以及變動范圍發生的可能性大小，如表6和圖7所示（以潛變量X1為例）。

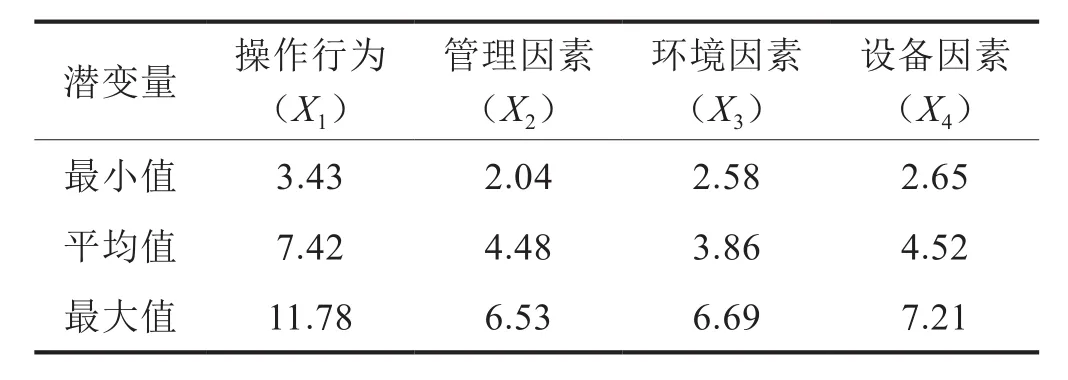
表6 潛變量的模擬值表

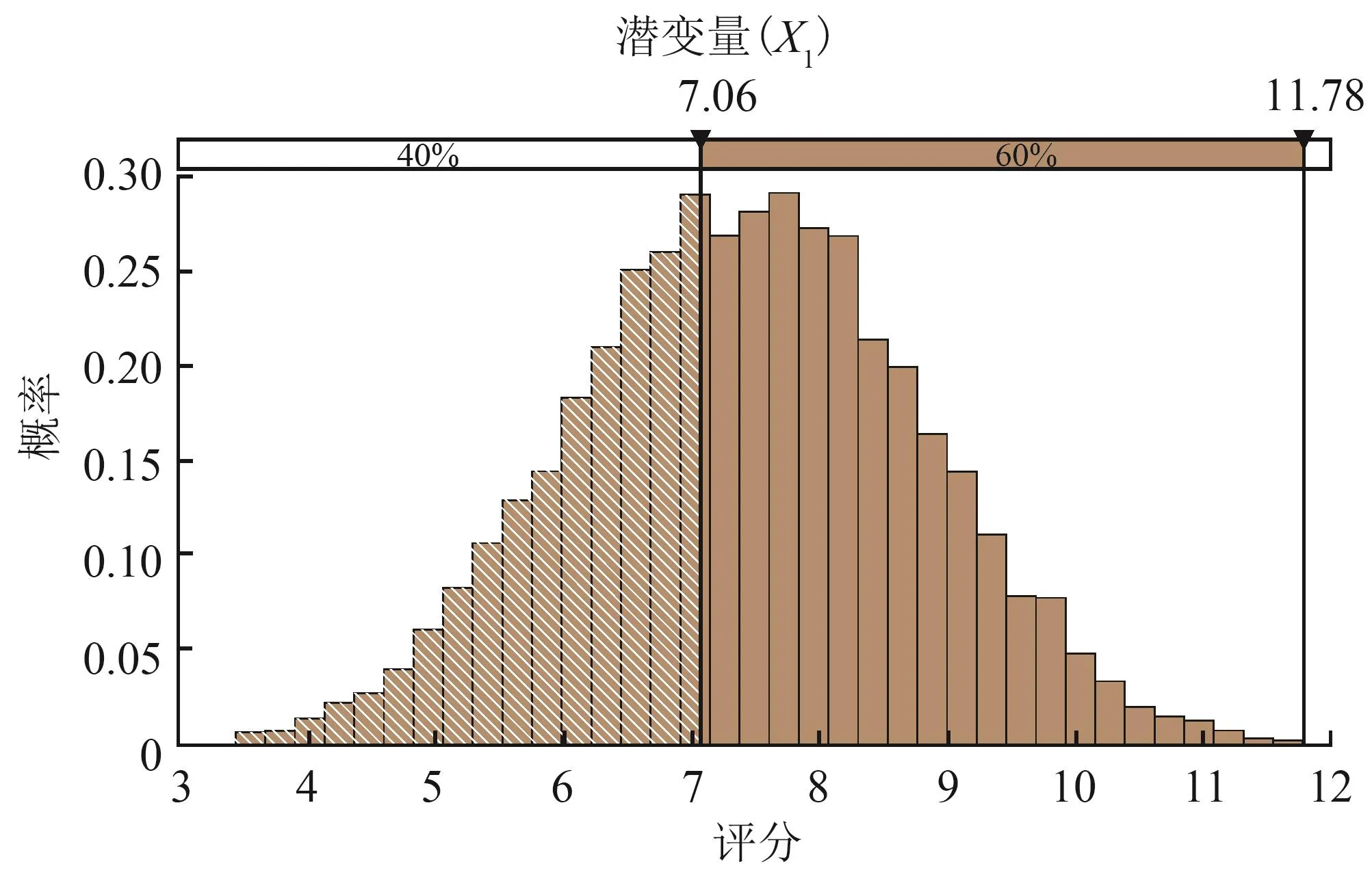
圖7 潛變量X1的模擬值隨機概率分布圖

由表6所示，結合事故后果程度得到風險評估新模型，最后生成該鉆井現場作業危險度的隨機概率分布和累積概率圖如圖8所示。由此可以知道鉆井風險的可能性結果以及每個結果出現的可能性，還可以得到一定置信水平下的現場作業風險范圍。根據正態分布函數，以風險置信區間[0 20%）、[20%40%）、[40% 60%）、[60% 100%）、[80% 100%）來劃分風險等級[17]，由正態分布函數數值表，可確定各風險等級的閾值區間于表7中。當置信度取40%時，計算得到的風險值范圍為[95 101]，故此范圍內的風險值是屬于安全范圍的。

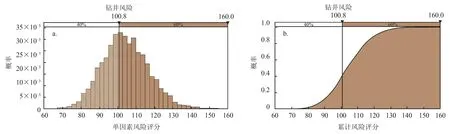
圖8 危險度隨機概率分布圖和累積概率圖

表7 SEM—MC的風險等級閾值表

利用MC模擬進行5 000次迭代計算后，得到模擬結果R = 108.9，結合表7，可知該鉆井現場作業風險處于一般等級，與實際情況相符。

3.2.2 與其他方法的對比

通過風險因子導致事故的可能性分值與事故后果指標分值的累積[17]，可以對鉆井現場作業進行評判，建立危險度模型由此確定的風險等級如表8所示。該鉆井現場作業的風險等級閾值與SEM—MC的方法存在不同，其風險等級閾值范圍比風險評估新模型更大，這可能是由于SEM—MC方法考慮了各風險因子之間的關系，使得彼此之間的可能性分值不存在疊加效應，避免了重復信息。此外，基于SEM的測量模型，MC模擬出潛變量的可能性分值，并結合危險度確定風險等級，使得評估結果更符合實際情況。

表8 R*[17]與SEM—MC風險等級閾值比較表

4 結論與建議

筆者首次提出了結構方程模型和蒙特卡洛模擬相結合的鉆井現場作業風險評價新方法，其評價結果可對鉆井作業現場作業安全風險管理具有重要參考作用。

1）通過結構方程模型確定了鉆井現場作業風險體系的指標權重，克服了無法確定各因子間的相關性以及權重的主觀性，此結構模型結合蒙特卡洛模擬求得危險度用以衡量風險等級，為鉆井現場作業風險評價提供一種新的評價方法。

2）根據結構模型可知，操作行為和環境因素對鉆井風險影響較小，而整個鉆井作業風險體系中管理因素占有最大的比例，說明管理層人員應該加強標準安全管理知識，要有超前的風險意識，讓操作人員有更好的保障，才能有效地減少人員安全事故的發生。

3）利用測量模型求得各風險因子的權重大小并找到關鍵風險因子。場所不符合要求和一般設備缺陷是兩個主要關鍵因子，其相關系數為0.57。操作行為的關鍵因子是常規勞保穿戴不齊，其與場所不符合要求的相關系數為0.35。說明對于員工在施工前進行安全教育是很有必要的，可以增強員工的安全意識。同時管理人員應注重與施工人員的溝通，對注意事項進行重點講解，防止不規范不安全行為發生。

4）基于蒙特卡洛模擬鉆井風險因子，根據每個風險變量的分布特征生成一系列符合要求的樣本數據，最終得到鉆井風險值的概率分布，使得評價結果更加貼切于實際情況。