渦軸發動機高速兩支點轉子不平衡識別

廖三豐

（1. 中國航發湖南動力機械研究所，湖南 株洲 412002；2. 航空發動機振動技術航空科技重點實驗室，湖南 株洲 412002）

高轉速是渦軸發動機轉子最典型特征之一，渦軸發動機燃氣發生器轉子采用的是高速兩支點轉子，即采用1-0-1支承結構，其工作轉速一般超過40000r/min，往往在二階臨界轉速以上。轉子不平衡微弱變化將產生較大的不平衡激振力，所以前后彈性支承采用的是擠壓油膜阻尼結構（SFD）。SFD的阻尼剛度表現出明顯的非線性特征，在轉子不平衡量識別過程中如何處理支承參數的非線性一直是一個較大的難題。

上個世紀70年代以來，發展了許多基于線性理論的無試重動平衡的方法[1-4]，無論是振型平衡法還是影響系數法都是建立在線性理論基礎之上的，動平衡技術通常需要多次啟動施加配重，此類方法都以降低轉子響應為目標，不關注轉子實際工作中不平衡量惡化規律，無法達到轉子全工作轉速內不平衡量的識別。在旋轉機械故障診斷方面，也無法準確考慮到支撐結構非線性因素的影響，轉子不平衡過大的情況只停留定性的層面上[5-7]。國內外已有大量關于轉子不平衡在線識別的研究，饒柱石[8]等基于參數識別、子結構模態分析及阻抗匹配原理，通過建立轉子——軸承系統頻響函數實現對轉子不平衡量在線識別，該方法在識別過程中因計算規模小而具有快速的特征。畢士華等[9]提出了一種考慮了油膜力的轉子不平衡量時域方法，該方法通過求解線性矩陣方程組，無法給出不平衡量具體分布及相位關系。張召翠[10]等基于遺傳算法開展非線性軸承參數及不平衡量參數識別。劉淑蓮等[11]采用全息譜技術提取轉子共頻分量，從而識別非線性系統的不平衡量。以上識別方法計算復雜、識別變量多，在渦軸發動機實際工程應用中難以推廣。

目前，在發動機整機動力學仿真分析研究中和轉子不平衡惡化的在線監控的工程應用中，缺乏一套高效的不平衡量識別都方法[12-13]。本文以彈性支承應力為目標函數，開展非線性支承參數下高速轉子不平衡量參數識別方法研究，實現了全工作轉速下轉子不平衡的“可視化”。整機試車中轉子振動測點布局受到發動機結構緊湊的制約，彈性支承應力值大小是為數不多較準確表征整機環境下高速轉不平衡響應狀況的振動信號。

1 渦軸發動機高速轉子不平衡特征

1.1 轉子非線性因素

渦軸發動機燃氣發生器轉子為典型的高速兩支點轉子，見圖1。在裝配中，中心拉桿上的一、二級壓緊螺母給整個轉子施加軸向預緊力，但在工作過程中會產生損失，主要表現在兩方面原因：一是發動機轉子在工作過程中，軸流壓氣機部分主要受到逆氣流方向的軸向力，渦輪部分受到氣流方向的軸向力，抵消了一部分預緊力；二是高速轉子的超高工作轉速，巨大的離心力會引起轉子變形，由于Poisson效應會造成零部件發生軸向收縮。變小的端齒壓緊力造成“壓不住”的情況發生，連接結構的不穩定，轉子不平衡量隨之發生非線性變化。

高速轉子前、后支承一般是帶有鼠籠式彈性支承的定心擠壓油膜阻尼器結構，其中結構形式見圖2，滑油通過供油孔進入供油槽，滑油在彈性支承與阻尼器之間的間隙中形成一圈油膜，轉子運轉產生偏心量，受擾動油膜產生的油膜力阻礙轉子發生偏心，流動的滑油把它 “吸收”的轉子振動動能“帶”出去。擠壓油膜阻尼器剛度阻尼參數理論推導方法常采用“短”“長”軸承假設，阻尼器長度與直徑之比小于0.25，兩端不封嚴時，采用短軸承假設，密封較好則采用長軸承假設，具體推導過程及計算公式在相關設計手冊已有推導，本文不再贅述。

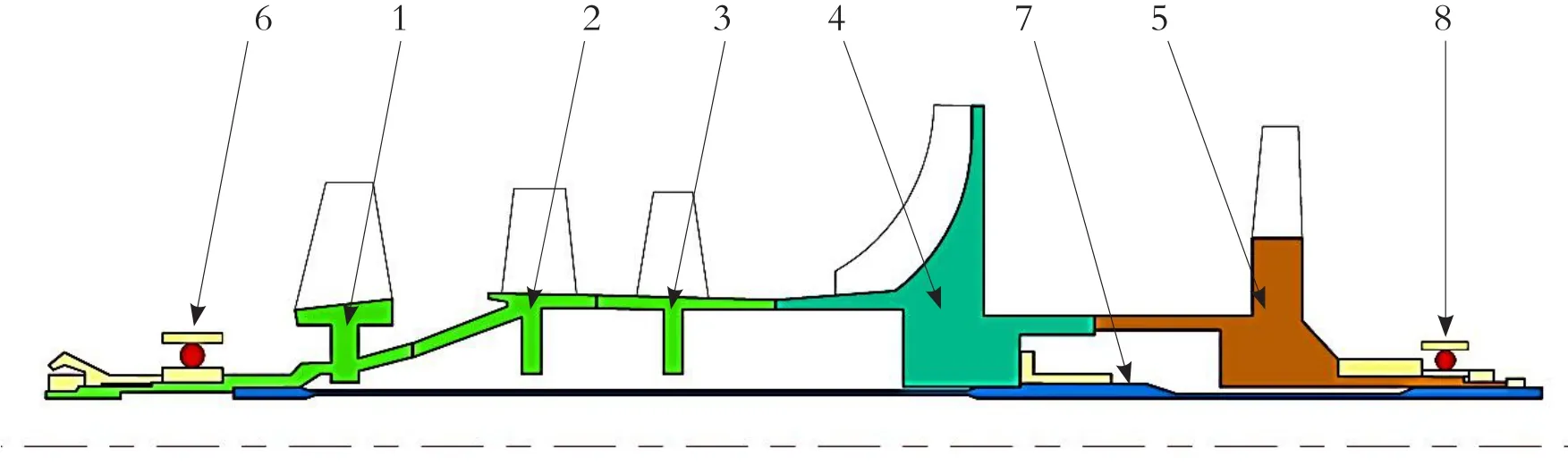
圖1 燃發轉子結構簡圖

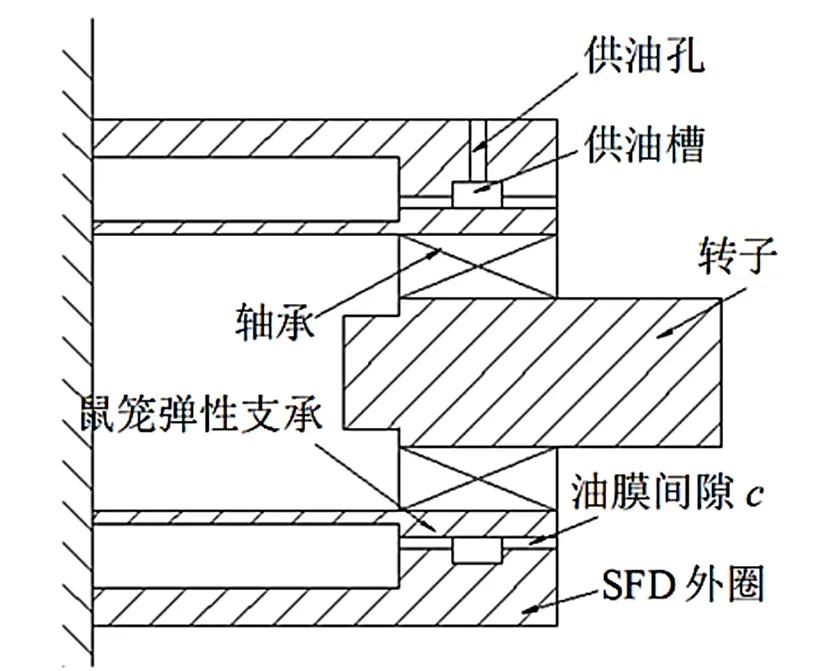
圖2 擠壓油膜阻尼器結構圖

帶有擠壓油膜阻尼器的高速轉子模型見圖3，K1、K2分別是前后支承剛度，Cs和Ks分別是擠壓油膜阻尼器阻尼與剛度。基于轉子試驗臺中振動數據的不平衡量識別過程中K1、K2采用彈性支承剛度，而基于整機試車中振動數據的轉子不平衡量識別中的K1、K2應包含機匣的剛度，是一個隨工頻變化的動剛度。剛度、阻尼的非線性會直接影響發動機轉子不平衡量識別的準確性。

圖3 轉子支承剛度阻尼模型

1.2 不平衡量識別中參數描述

考慮動剛度及非線性油膜剛度阻尼的轉子運動方程可以寫成以下形式

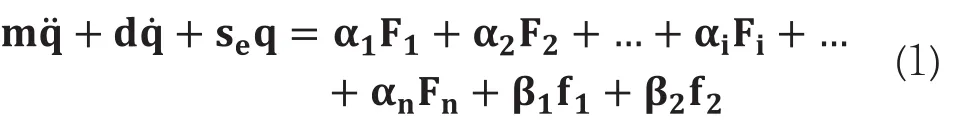
式中，q為轉子廣義坐標系矩陣，m為高速轉子系統質量矩陣，d為包含系統內阻尼和陀螺力矩矩陣，se為包含系統動剛度的矩陣。為減小篇幅，以下參數介紹不帶下標，α為待識別不平衡量位置矩陣（一般選取轉子動平衡去材料界面位置），F表示不平衡力，β為擠壓油膜阻尼器位置矩陣，f為油膜力。為減少參數識別變量，se通過前期的計算得到，而擠壓油膜阻尼器剛度阻尼通過試驗實測或理論公式計算得到，至此方程中待識別參數為F。轉子工作狀態下的不平衡力主要表現為工頻激勵。將不平衡力Fi沿水平和豎直方向分解，所得到的不平衡力表達式為

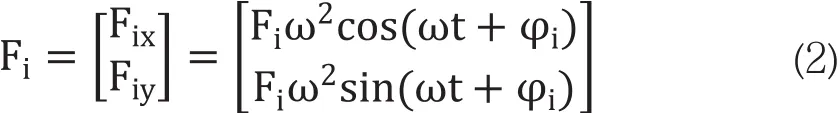
其中，Fi為不平衡量大小，ω為轉子工作轉速，φi表示不平衡量角度。本文轉子不平衡識別主要用于整機動力學研究的變量輸入，不涉及動平衡試驗，則各位置等效不平衡量周向角度關系以相對角度表示。則(1)式可描述為

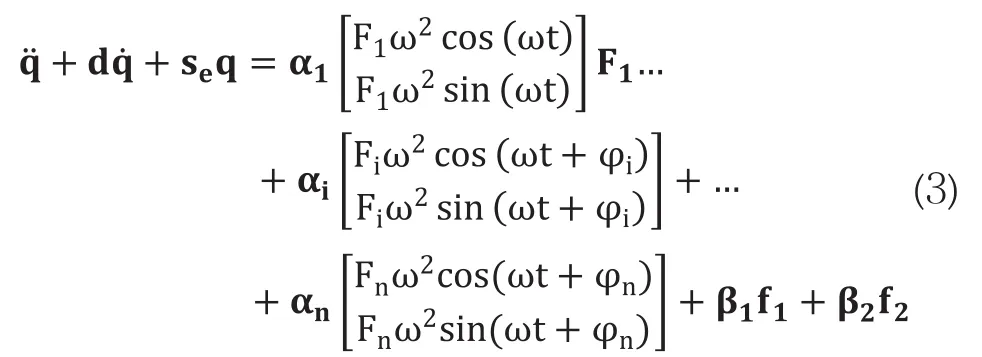
(3)式中待識別不平衡待識別參數為Fi與φi，共計 2n-1 個。

渦軸發動機整機環境中的鼠籠彈性支承肋條應力水平是最能直接表征轉子不平衡狀態的試驗值。圖4為典型渦軸發動機鼠籠彈性支承結構，軸承旋轉載荷作用下，肋條應力σ矩陣是轉子軸承位置位移響應q矩陣及位移角度ψ的函數，描述為

圖4 彈性支承結構

求解在一個轉子旋轉周期內彈性支承應力矩陣的有效值得到σeq，同樣提取軸承位置位移響應矩陣有效值qeq，則式(4)式可變為一個與位移角度無關的函數表達式

矩陣σeq為參數識別的目標函數變量。

至此，參數識別中的自變量及目標函數已經明確。

2 轉子系統參數識別

采用建立起的高速轉子ANSYS有限元模型，基于ANSYS開展支承參數識別，并以ISIGHT為平臺，開展發動機轉子不平衡量識別參數識別。

2.1 支承參數識別

當擠壓油膜阻尼器結構確定后，其Cs和Ks是供油壓力、滑油粘度、轉子工作轉速、和偏心率函數。一般情況下，供油壓力和滑油粘度是確定的，工作狀態下的Cs和Ks僅是轉子工作轉速及偏心率的函數。基于ANSYS非線性支承參數轉子不平衡響應計算流程見圖5，通過不斷“修正”支承剛度、阻尼使轉子不平衡響應達到一個穩定值。由于試驗數據的離散性，識別過程中基于實測擠壓油膜阻尼器Cs和Ks數據采用線性插值獲取。每次迭代得到的擠壓油膜阻尼器剛度阻尼帶入到動力學有限元模型中即可計算得到支撐位置的油膜力，代入到（1）式即可實現對動力學方程的求解。

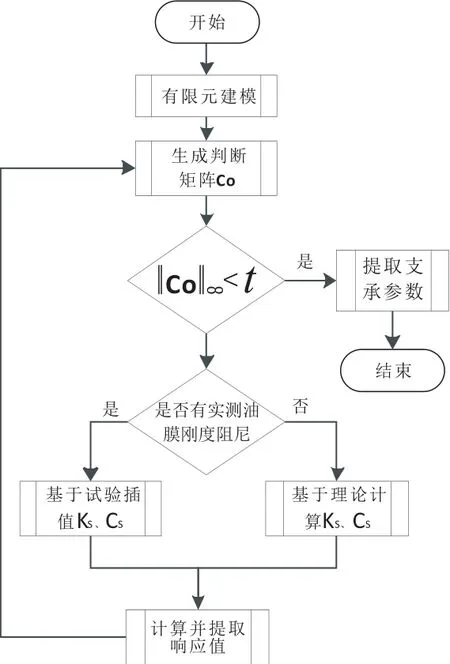
圖5 支承參數識別流程

2.2 不平衡量識別

轉子不平衡量識別過程可歸結為優化問題。基于公式（4），獲取支承位置位移響應有效值，化彈支應力實驗數據為支承位置位移響應數據。參數識別過程的數學模型可描述為

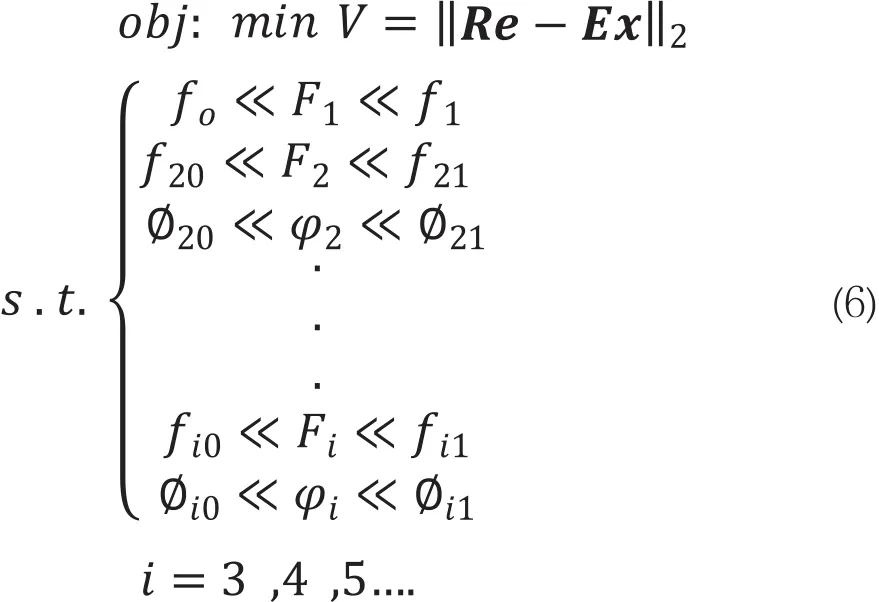
數學模型中：Re表示仿真獲取的彈性支承位移響應有效值向量；Ex表示試驗中支承位置位移響應有效值向量；V表示仿真值向量與計算值向量之差的2范數；F表示待識別的不平衡量；f表示變量上下邊界；φ為不平衡量相對相角；?表示相對相角上下邊界，一般情況下取0～2π。

由于轉子支承參數的高度非線性，本文選用Pointer優化器，該求解器能夠高度非線性和非連續性設計空間問題，通過自動捕捉設計空間的信息，然后靈活的組合算法形成一個參數識別策略。Pointer優化器包括的算法有：是線性單純形法（linear simplex），序列二次規劃法（sequential quadratic programming），最速下降法（downhill simple）和遺傳算法（genetic algorithms）。

3 算例研究

以某渦軸發動機高速轉子為不平衡量識別對象，該轉子為3A+1C壓氣機結構，一級燃氣渦輪，轉子支點跨距為495mm，轉子總質量為20.3030 kg，軸慣性矩Ixc=62848.30 kg·mm2，直徑慣性矩 Iyc=429375.08 kg·mm2，Izc=429375.08 kg ·mm2。基于ANSYS建立該轉子梁單元有限元模型，見圖6。

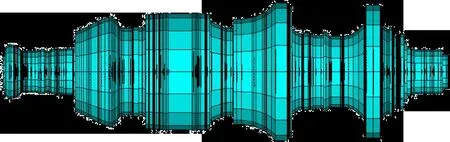
圖6 高速轉子梁單元模型

通過仿真分析發現，工作過程中，彈性支承處于彈性變形階段，其應力有效值σeq和軸承位置位移響應qeq呈線性關系。建立起前后支承彈性支承有限元分析，計算得到σeq=h(qeq)函數關系

高速轉子前后彈性支承剛度分別為1.72×107N/m和2.15×107N/m，擠壓油膜阻尼器參數見表1，其中滑油滑油密度ρ=904 kg/m3，運動粘度υ=4.2×10-6m2/s。

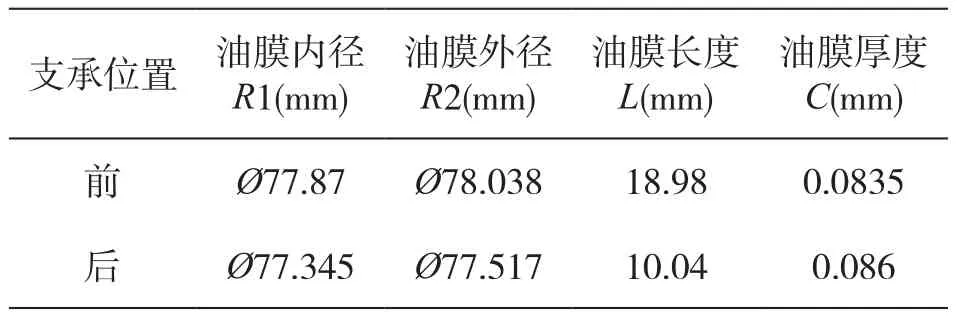
表1 轉子前后支承參數

以轉子一級壓氣機盤及渦輪盤為等效不平衡量識別位置，式（2）中轉子基頻分量，前后平衡截面等效不平衡力分別為：。本算例中待識別參數為一級壓氣機盤處等效不平衡量渦輪盤處等效不平衡量和相對相角

以該轉子在轉子試驗臺上試驗數據為目標，彈性支承水平與垂直肋條上應力值相當，提取轉速 32900 r/min、36000 r/min、38000 r/min、41600 r/min和42500 r/min轉速下轉子彈性支承水平肋條上應力有效值見表2。基于式（4）轉換得到圖7，該轉子彈性支承應力隨轉速先增加，而后呈減小趨勢。高速轉子為典型的剛性轉子，轉子工作轉速位于二階擺動到三階彎曲轉速之間，轉子工作轉速、不平衡量和油膜力是轉子臺上彈性支承應力發生變化的主要影響因素。

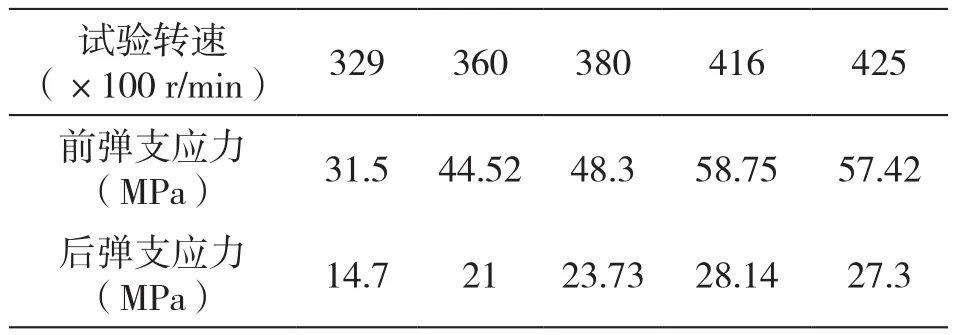
表2 彈性支承水平肋條應力

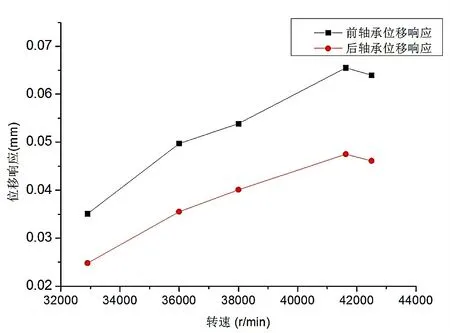
圖7 軸承位移響應有效值

本算例采用的仿真計算機為Intel i5四核處理器，主頻3.4 GHz，8 GB內存容量。

在識別程序中輸入轉速、前后軸承位移響應有效值，以F1、F2和φ為待識別參量，開展不平衡量識別研究。為減小篇幅，本文只列出轉速32900 r/min下轉子不平衡量識別過程，在參數識別程序中分別輸入前、后軸承位移響應。以前、后支承位移響應為目標的識別過程見圖8～圖9，每個迭代步中嵌套有圖5中支承參數識別流程，不同平衡量下識別的油膜阻尼、剛度也存在差異性，整個不平衡量及支承參數識別過程約7 min，其他轉速下識別時間為5～10 min。

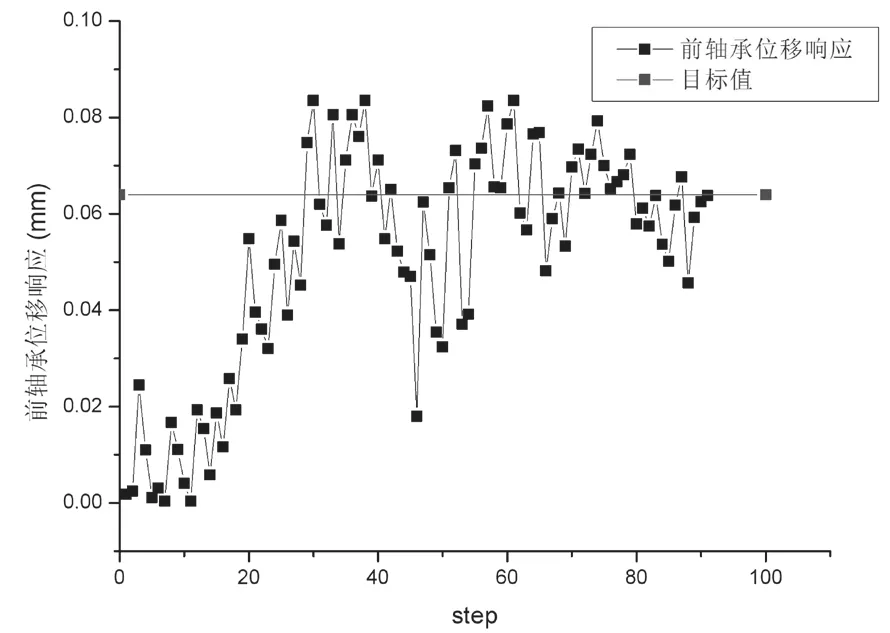
圖8 前支承位移響

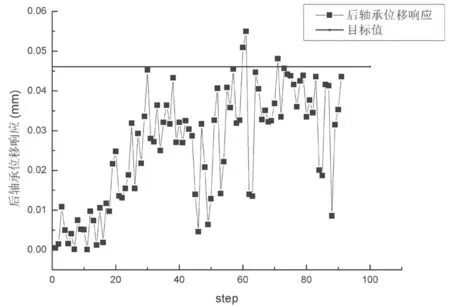
圖9 后支承位移響應

表3 彈不平衡量識別結果

?

輸入其他轉速及對應的目標值，識別結果見表3，繪制工作轉速內轉子不平衡量變化曲線圖，圖10表明，轉子不平衡量隨高速轉子轉速上升呈現放大的趨勢，高速轉子前、后不平衡量相對相角約180度。

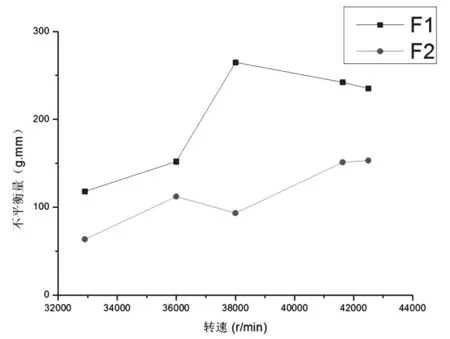
圖10 全工作轉速內不平衡量變化

通常情況下，該類轉子裝機前不平衡量會控制在一定標準范圍內，經過一輪試車之后，對運轉后的轉子做不平衡量測試，不平衡量往往會出現不同程度的放大，根據筆者的工程經驗，轉子不平衡量最大可放大數十倍。通過本算例的研究發現，工作中的轉子不平衡量比裝機前需用不平衡量放大了10倍到20倍左右。

4 結論

本文建立起渦軸發動機高速兩支點轉子有限元動力學模型，選取轉子動平衡位置處等效不平衡量及相對相角為待識別變量，面向轉子彈性支承肋條應力的工頻信號，基于ANSY編寫擠壓油膜阻尼器阻尼、剛度識別程序，基于ISIGHT軟件采用Pointer求優化器完成渦軸發動機高速兩支點轉子不平衡量的識別，研究發現：

1)本文所提出的不平衡量識別方法識別效率較高，在文中的算例中，單個工作轉速下不平衡量識別的時間為5～10min，該方法在工程設計中具有較強的可操作性；

2)識別結果表明工作中的轉子不平衡量會發生不同程度的放大，本文的算例研究發現，該方法識別的結果能反映轉子在工作轉速內不平衡量變化趨勢。

本文所識別得到的結果可作為整機振動仿真分析的輸入條件，為發動機整機不平衡響應研究中的不平衡量的施加提供參考。