木材徑切面內部缺陷的應力波成像算法
鄭澤宇, 馮海林, 杜曉晨, 方益明
(1.浙江農林大學 信息工程學院,浙江 杭州311300;2.浙江農林大學 浙江省林業智能監測與信息技術研究重點實驗室,浙江 杭州311300;3.浙江農林大學林業感知技術與智能裝備國家林業和草原局重點實驗室,浙江 杭州311300)
木材的內部缺陷會嚴重影響木材的質量。由于應力波的木材無損檢測成本低、攜帶方便及對木材無損的特性,使得其越來越受到人們的青睞。國內外已開展了應力波速度與木材內部缺陷之間的相關研究。如WANG[1]通過應力波在缺陷木材中的傳播規律,表明應力波在腐爛或劣化的木材中比在完好的木材中傳播速度慢。徐華東等[2]以校園內的活立木作為樣本,使用應力波檢測儀器對校園樹木進行二維成像,表明在活立木的斷層橫截面上,應力波橫向的波速要小于徑向的波速,且應力波在木材內部的波速受制于木材內部的缺陷情況。國內學者也對應力波無損檢測儀器的可行性進行了研究。楊學春等[3]利用應力波檢測儀器對原木內部腐朽進行了研究,結果表明:應力波測試儀能準確判斷不同樹種原木內部的腐朽程度,并且能夠得到原木內部腐朽基本形狀的二維圖像。LIN等[4]運用應力波斷層成像技術,對不同大小的樟樹Cinnamomum camphora人造空洞進行了研究,表明應力波斷層成像技術可以反映木材的空洞大小及位置,驗證了應力波無損成像技術的可行性。以上研究主要針對應力波傳播規律與成像技術的應用領域,但對應力波成像算法的研究不多。FENG等[5]提出了一種基于插值的圖像重建算法,利用周圍點的值估計未知點的速度情況,進而重建樹木內部缺陷圖像。DU等[6]提出了基于橢圓的空間插值以及速度補償的方法對木材的橫截面進行成像,能夠準確地判定缺陷位置,并得到了良好的成像效果。國內外對于應力波在樹木內部的傳播規律做了大量的研究[8-10],但是對于木材徑切面傳播規律和成像方法研究還比較少。翁翔等[7]利用無損檢測儀器對木材的徑切面進行測量,對應力波橫向速度和徑向速度的比值進行了回歸,得到了應力波在木材徑向上的傳播速度模型,其結果的擬合度較高。但在木材徑切面的缺陷成像方法研究較少。鑒于此,本研究基于應力波在木材徑切面中沿直線上傳播的假設,提出一種木材徑切面內部缺陷的速度修正成像方法。
1 應力波木材徑切面成像原理
1.1 樹木徑切面模型的建立
木材可以用圓柱體來近似的表示,那么木材的徑切面可以被抽象成一個近似的矩形模型,將n個(n一般為12)傳感器放置于被測樹木兩側(傳感器1至n/2位于同一側)。每個傳感器距離地面的高度(或者某一水平高度的距離)分別為(H1,H2,H3, …,Hn);S1~Sn表示應力波傳感器,傳感器按照從右向左,呈U字形進行放置;D表示樹木直徑;θjk為每個傳感器兩兩之間的相對角度。如圖1所示:定義一個坐標系表示樹木徑切面。
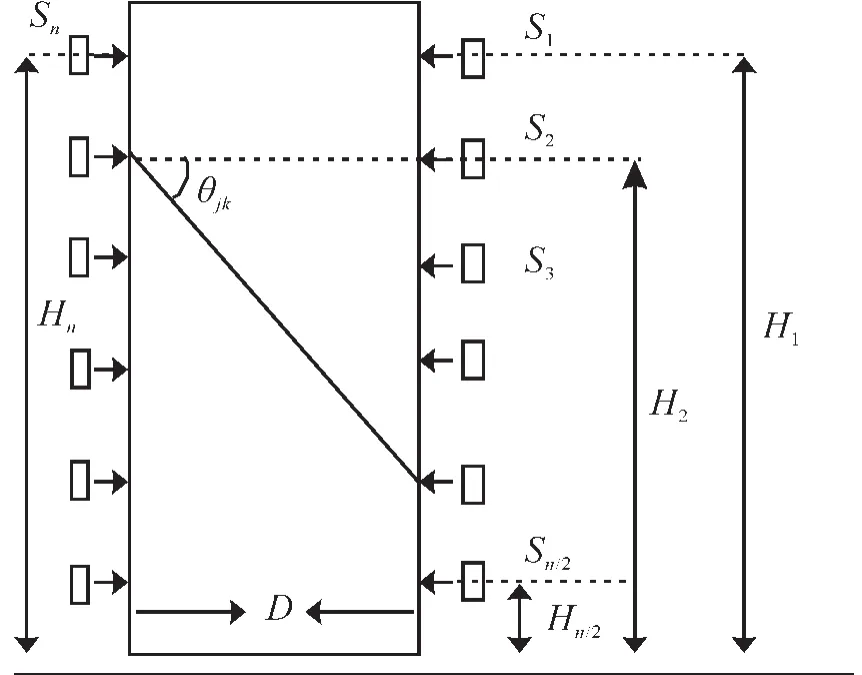
圖1 木材徑切面模型Figure 1 Radial and longitudinal plane model of wood
令Sn/2+1所在的位置為原點坐標,建立傳感器的坐標系。
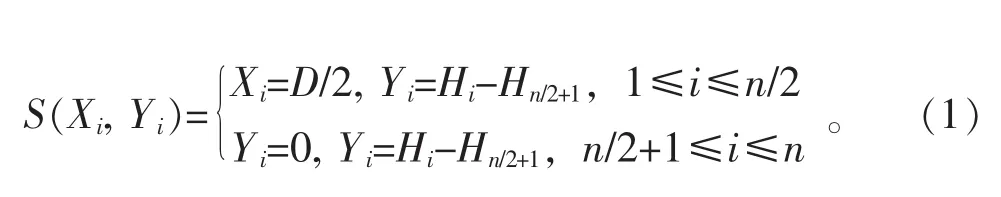
式(1)中:有1≤i≤n,Xi表示傳感器位置橫坐標,Yi表示傳感器位置縱坐標。根據每個傳感器的位置數據,可得到每個傳感器兩兩之間的相對角度θjk為:

式(2)中: 1≤j≤n/2,n/2+1≤k≤n。
假定應力波在木材中是沿著直線傳播的,通過傳感器間的距離和應力波傳播的時間計算出傳感器間應力波的傳播速度[11]。
1.2 速度修正插值方法
為了預測木材離軸的單軸壓縮強度,Hankinson公式[12]給出一種數學模型。當應力波在木材徑切面上傳播時,如果傳播方向與垂直于木材紋理角方向所成的角度為θ,那么根據Hankinson公式可以推出如下公式:

式(3)中:V1表示平行于紋理方向上的應力波傳播速度;Vr表示垂直于紋理方向上的應力波傳播速度;θ表示傳播方向與木材紋理方向所形成的角度;Vθ表示在角度為θ時應力波在木材徑切面上的傳播速度。
翁翔等[7]通過計算得出:


根據式(5),可以得出:


就可以得出速度修正的公式:

式(7)中:Vc(θjk)表示修正后的速度;Vd(θjk)表示為測量得到的應力波傳播速度;k是常數;θjk表示2個傳感器間與垂直于木材方向紋理所成的角度。
因此經過缺陷區域的Vα經過速度修正后,就可以反映出應力波經過缺陷區域速度呈現出降低的現象,有效地減少了由木材的各向異性[13]導致的應力波在木材不同方向上傳播速度不一致現象的影響,為木材內部缺陷成像提供更精確的數據。
將通過傳感器之間的線速度VL轉換成木材徑切面上交點的速度VP:

式(8)中:VL1至VLn分別表示每條經過該交點的應力波傳播路徑上修正后的線速度;(VL1,VL2,…,VLn)∈Vc(θjk)。

圖2 應力波在不同缺陷程度的木材中傳播Figure 2 Stress waves propagate in wood of different defect degree
利用速度修正插值法對木材的徑切面進行成像。每個已知點都對插值點具有一定的影響,即權重[14]。權重隨著已知點和插值點之間距離的增加而減弱,距離插值點越近的已知點的權重越大。而且當已知點在距離插值點一定范圍以外時,權重可以忽略不計。在任一待插值點的值是鄰域內已知點權重之和。可以表示為:

式(9)中:Vqi為待插值點的預估值;V′Ln為每條經過該交點的應力波傳播路徑上未修正的線速度,(V′L1,V′L2,…,V′Ln)∈Vd(θjk);θLn表示每條經過該交點的應力波傳播路徑與水平面的所成的夾角, (θL1,θL2,…,θLn)∈θjk;di為第i個已知點與待插值點的距離;n表示鄰域內參與插值計算的已知點的個數;m為常數。
成像算法步驟:
步驟1:初始化(建立木材徑切面的模型,輸入傳感器的坐標(x,y),計算傳感器間的線速度Vd(θjk);
步驟2: 利用式(7)求出修正后的線速度矩陣Vc(θjk);
步驟3:傳感器兩兩連線的交點坐標(xc,yc),將鄰域內已知屬性值的交點的坐標以及每個交點對應的線速度V′Ln代入式(8)計算Vp的屬性值;
步驟4:通過將已知點的屬性值代入式(9),計算未知點的屬性值;
步驟5:重復步驟4,直到計算出所有徑切面上的每個點的屬性值。
步驟6:將預估點根據屬性值的不同進行不同顏色的賦值,并生成二維圖像。
2 實驗材料與方法
實驗用于采集木材應力波數據的儀器是Fakopp。如圖3所示:將傳感器分別放置在原木徑切面兩邊,每邊6個傳感器,總共12個。實驗過程中使用檢測儀器自帶的重錘以相同的力度,垂直于傳感器方向,對各個傳感器分別敲擊3~5次,采集總共36~60組數據。將數據用于下文的成像中。

圖3 應力波測量裝置與傳感器的布置Figure 3 Stress wave measuring device and sensor arrangement
本實驗樣本編號、樣本種類、樣本周長、樣本測量高度等信息如表1所示。
對樣本的空洞面積測量方法如下:利用卷尺測量樹木空洞的長和寬,假設樣本的長為L,寬為W,則對于長方形的空洞缺陷面積SR計算公式為:

假設梯形的空洞,上底長度為A,下底長度為B,缺陷的高度為H,梯形的空洞的面積ST則用公式可以表示為:


表1 實驗樣本基本信息Table 1 Experimental sample information
假設圓形的缺陷孔洞的直徑為R,那么缺陷的面積SY可以表示為:

3 結果與分析
3.1 速度修正插值法(VCI)與反距離加權插值法(IDW)成像結果對比
從圖4A可以看出:缺陷為人工挖掘并且形狀為長方形。如圖4B所示:未修正的線圖將經過缺陷區域的線段表示為黃色,未正確區分缺陷區域。圖4C表示的是修正后的線圖,將經過缺陷區域的線段(如1號和7號、2號和8號等傳感器之間的連線)錯誤地表示為缺陷顏色紅色。從圖4D可以看出:使用IDW的成像結果,只能粗略反映缺陷位置,對于缺陷大小與形狀都不能進行準確成像。對比VCI的成像結果圖4E,VCI可以較好還原缺陷位置,可以看出缺陷的位置是處于第3號、5號與8號、10號傳感器之間,與圖4A所示的真實缺陷位置基本吻合。但是對于缺陷形狀的成像不夠準確。
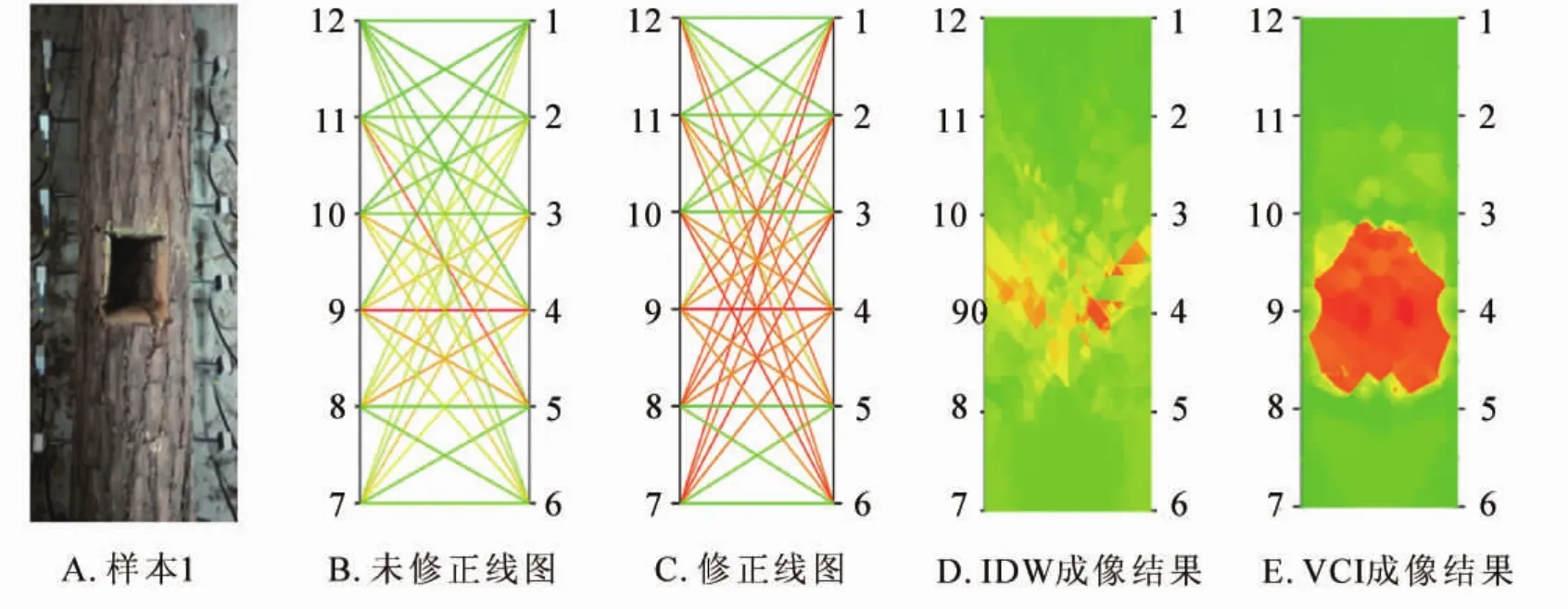
圖4 雪松樣本實驗結果Figure 4 Sample experiment results of Cedrus deodara sample
從圖5A可以看出:樣本缺陷位置處于右邊2號至5號傳感器的下面3 cm,以及左邊11號傳感器至7號傳感器的下面3 cm的位置,形狀為矩形。從未修正線圖(圖5B)可以看到:僅有少部分經過缺陷區域的線段被表示為缺陷的紅色,大部分經過缺陷區域的線段被表示為非缺陷的綠色。修正后的線圖(圖5C)較好地區分缺陷區域,并以不同的顏色進行區分。可以看到IDW的成像結果雖然能夠還原缺陷的位置(圖5D),但對缺陷還原的準確度較低,對缺陷位置和大小的還原參考價值較低。如圖5E所示:VCI的成像結果可以較好地反映缺陷位置,但存在對缺陷區域成像結果比真實結果偏小的情況,以及對缺陷邊緣的重建不夠平整,對于樣本的缺陷輪廓可以較好還原,可以反映樣本的缺陷特征。
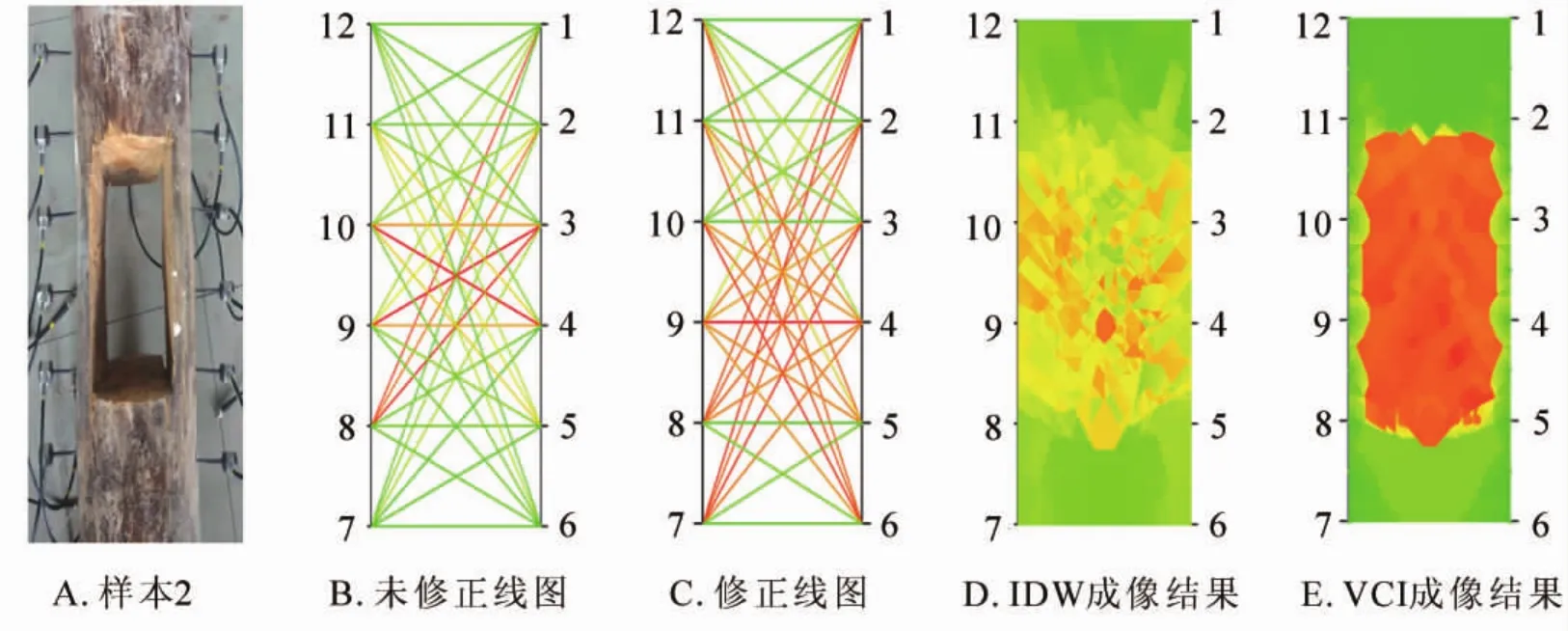
圖5 泡桐樣本實驗結果Figure 5 Sample experiment results of Paulownia fortunei sample
從圖6A可以看出:樹木的缺陷位置位于右邊的3號和4號傳感器之間,以及左邊的9號和10號傳感器之間。對比圖6B與圖6C可以看到:未修正的線圖將經過缺陷區域的線段(如7號、1號傳感器線段以及6號、12號傳感器線段)錯誤地表示為經過正常區域的線段,呈現綠色,與真實情況不符。而修正后的線圖,能夠較好區分缺陷部位。從IDW成像結果(圖6D)反映缺陷所處的低速度區域,但對于缺陷的形狀無法正確成像。缺陷成像結果呈現不規則的塊狀分布,無法反映樣本的缺陷特征。VCI的成像結果(圖6E)顯示:缺陷形狀呈現一個類似圓形的不規則形狀,與真實的缺陷形狀較為接近。成像結果表明缺陷位于3號、4號傳感器與9號、10號傳感器之間,與圖6A的真實缺陷位置也基本相同。

圖6 樟樹樣本實驗結果Figure 6 Sample experiment results of Cinnamomum camphora sample

表2 缺陷與預測的4種組合Table 2 Four combination of real defects and predict defects
3.2 成像結果誤差分析
使用混淆矩陣法對成像效果進行定量的誤差分析,混淆矩陣包含由分類系統完成的實際和預測的分類信息[15]。 FAWCETT[16]描述了真、 假分類系統中 4 種可能組合(表 2)。
從表2的矩陣可以推出的常用度量值[17],如準確率或者正確率(A),精確度(P)和查全率(R)。

式(13)~(15)中:準確率A表示對木材狀態預測正確的百分比;精確度P表示對木材缺陷預測的可靠性水平高低;查全率R表示對木材缺陷的預測能力高低;C,W,E和F所代表含義見表2。
從表3可見:3個樣本的準確率A為72.32%~95.85%。使用VCI方法的3個樣本的平均準確率為93.34%,使用IDW方法的3個樣本平均準確率為82.63%。IDW方法在1號、2號樣本中的準確率均大于85.00%,其原因應該是IDW方法在成像結果中雖然不能很好地反映木材缺陷的特征,但是對木材完好的部位成像結果較好,所以得到較高的準確率。而3號樣本只有72.32%的準確率,對比真實缺陷可以看出:IDW方法將部分正常木材錯誤地成像為缺陷木材,所以導致準確率下降。IDW和VCI的準確度標準差分別為7.38%和2.04%。可見,VCI在準確率上的標準差較小,說明VCI方法在不同樣本中的準確率結果更穩定,準確率相較于IDW方法均有所提高。

表3 不同樣本的準確率Table 3 Accuracy of different samples

表4 不同樣本的精確度Table 4 Precision of different samples
從表4可見:3個樣本的精確度P為65.79%~88.35%。使用VCI方法的3個樣本的平均精確度為82.26%,使用IDW方法的3個樣本平均精確度為70.19%。VCI方法中3號樣本的結果要好于其他樣本,其原因是3號樣本中的預測缺陷大部分與真實缺陷重合,且預測缺陷大部分落在真實缺陷上,所以得到較高的精確度。IDW和VCI方法的精確度標準差分別為5.00%和4.70%。VCI方法在準確度上的標準差較小,VCI方法在精確度的穩定性略高于IDW方法。同時VCI方法在不同樣本上的精確度均好于IDW方法。
從表5可見:3個樣本的查全率R為17.98%~94.03%。使用VCI方法的3個樣本的平均查全率為92.65%,使用IDW方法的3個樣本平均查全率為36.64%。VCI方法中的查全率高于IDW方法。可見,VCI方法可以較好地反映木材的真實缺陷結果,且對木材的缺陷位置成像結果更好。在真實缺陷大小不變的情況下,由于VCI方法可以更好地反映木材的缺陷情況,因此得到了更高的查全率,與真實的成像結果相吻合。IDW和VCI方法的查全率標準差分別為:15.59%和1.93%。說明VCI方法的查全率標準差要遠小于IDW方法,在查全率的穩定性上要好于IDW方法。

表5 不同樣本的查全率Table 5 Recall rate of different samples
4 結論
本研究提出了一種應用于木材無損檢測領域的,基于應力波的木材徑切面成像方法。通過與IDW的成像效果比較發現:不論是在定量還是定性方面,VCI方法對木材徑切面的缺陷成像結果都好于IDW方法。與真實的缺陷進行對比得到較小的誤差,可以準確反映木材內部的真實缺陷情況,具有較高的成像精度。利用傳感器測量得到的不同應力波數據,通過對不同缺陷的樣本進行實驗,驗證了該算法對于木材的徑切面成像效果的可行性。利用混淆矩陣對成像結果進行了定量分析發現:VCI方法的平均準確度為93.34%,平均精確度為82.26%,平均查全率為92.65%,均高于IDW方法,但對于缺陷具體形狀的成像結果,其準確度有待進一步提高。

