基于數形結合思想的初中數學教學策略探究

湖北省南漳縣城關鎮胡營中學 張鴻飛

一、運用數形結合思想的意義

數形結合思想的運用需要注意以學生為主體，以培養學生數學思維為基礎，滿足新課程改革對現代教育提出的要求。數形結合在教學中要結合數學實例向學生講解滲透，加強學生對數學的重視程度，培養學生的數學素養以及能力。數形結合方法體現在數學的各種題型中，考查學生對數學的理解，所以在數學教學中，讓學生深入理解并且掌握數形結合是非常重要的。

數形結合可以培養學生的多方面能力，例如學生在多次運用圖形解題之后，再遇到類似題目時，便會在大腦中形成自己的直覺，較快地反應出題目對應的圖形，省去了一步一步的分析，節約了做題時間。例如很多函數的學習是很抽象的，在加入圖象之后，可以幫助學生理解函數這樣抽象的概念，鍛煉學生的抽象思維。再例如在平面向量的學習中可以加入圖形，讓學生在理解平面向量的基礎上向空間向量延伸，培養學生的發散思維。

二、數形結合思想下的初中數學教學策略

1．集合問題

例題：某班級中有男生共63個人，其中喜歡打網球的有35個人，喜歡打籃球的有27個人，兩項運動都喜歡的有5個人，那么這兩項運動都不喜歡的有幾個人呢？我們運用數形結合解決本道集合問題時，可以利用韋恩圖，如下圖所示，用圖中的小圓形代表喜歡打籃球的27個人，大圓形代表喜歡打網球的35個人，兩個圓形交集的地方代表喜歡這兩項運動的5個人，則除去已知人數的圖形部分，陰影部分就是這兩項運動都不喜歡的人數。計算如下：63-（35+27-5）=6（人）。

在數學集合問題中，如果學生只靠單純地運算是很容易多加（減）、漏加（減）的，但是數形結合的運用能夠將題目中的已知條件直觀地表現出來，這樣就使學生的思路非常清晰，減少運算錯誤，而且運用圖形解答此題，也會降低這類題型的難度，讓學生更容易理解集合問題。

2．函數問題

在初中教材一元二次方程的講解過程中運用數形結合思想，一般地，當a＞0（a＜0）時，則方程y=ax2+bx+c的圖象是一條開口向上（下）的拋物線，此時的圖象具有最低（高）點，當x=-時，方程y=ax2+bx+c具有最小（大）值y=。

例題：根據y=ax2+bx+c(a≠0)的圖象（如下圖），回答下列問題：①寫出方程ax2+bx+c=0的兩個根；②寫出y隨x的增大而減小的自變量x的取值范圍。

根據數形結合思想，圖象可知，①使方程成立的兩個根為x1=1，x2=3；②y隨x的增大而減小的圖象在對稱軸的右側，所以自變量的取值范圍為x＞2。

由此可知，在函數問題中加入數形結合思想是將抽象的函數知識轉化為直觀的圖象，便于學生的記憶與理解，也能在做題時幫助學生簡化問題，讓學生更容易理解函數問題。

3．幾何問題

例題：已知一條直線過點（-3，0），求當這條直線l與單位圓有兩個交點的時候，這條直線l的斜率k的取值范圍。根據題意，我們可以結合數形結合思想畫出這條直線與單位圓相交的圖象，如下圖所示，此時我們可以求出過點（-3，0）的兩條直線的斜率，，所以可得出k的取值范圍為-。

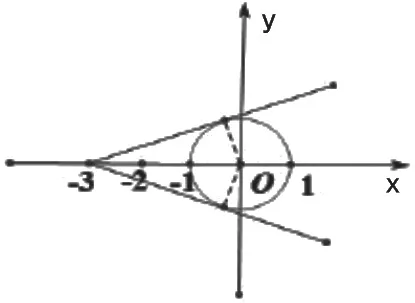
在幾何問題中運用數形結合思想即將抽象的幾何圖案用直觀的圖象表示出來，便于學生理解距離、斜率等問題，也可使復雜的幾何問題簡單化，以此增加學生解決數學問題的信心，也可激發學生學習數學的興趣，培養學生的數學思維。

總之，數形結合思想在初中數學教學中的應用，可以將復雜變簡單、抽象變直觀，在很大程度上幫助學生提升數學思維，所以，老師要加強對數形結合思想的重視，在教學中將數形結合灌輸到學生的大腦中，以此增加學生的信心，提高學生的學習成績與解決數學問題的能力。但是，并不是所有的問題都可以運用數形結合思想，老師一定要注意，不能讓學生將數形結合作為解決一切數學問題的萬能鑰匙，要懂得靈活運用，才能在此基礎上更好地發展。