非差模型與雙差模型的定位精度比較

崔 陽，苗亞哲，辜文杰，杜偉平，魏佼琛

(1.陸軍勤務學院，重慶 401331； 2.信息工程大學，河南 鄭州 450052)

以美國全球定位系統(Global Positioning System, GPS)、中國北斗導航衛星系統(BeiDou Navigation Satellite System，BDS)等為代表的全球導航衛星系統(Global Navigation Satellite System, GNSS)在交通運輸、航空航天等領域得到了廣泛應用。在GNSS精密數據處理中，以雙差模型為基礎的基線網解模式是常用方法之一[1-4]，但隨著多頻多模和測站規模增加，基線網解計算時間呈指數級上升。為了打破雙差網解模式的計算瓶頸，有學者提出了以非差模型為基礎的精密單點定位(Precise Point Positioning, PPP)模式[5-7]，其單站處理模式即可獲得測站絕對坐標，計算效率高，顯著降低了大網數據處理的計算時間。文獻[8]從理論上證明了雙差網解和PPP解的模型等價性，文獻[9]對非差與雙差模型進行了對比，指出非差模型通過精確的誤差改正可實現厘米級甚至毫米級的靜態定位結果。作為高精度GNSS數據處理中常用的兩種數學模型，雖然許多學者在理論上證明了雙差模型和非差模型的等價性，但由于誤差源的改正通常是采用經驗模型，且非差模型直接得到絕對坐標而雙差模型需要引入坐標基準才能獲得絕對坐標，對于精度要求較高的參考框架維持、地殼運動和變形監測等應用領域，非差模型或雙差模型進行數據處理是否精度一致還需進一步研究驗證。本文選取國際地球參考框架(International Terrestrial Reference Frame, ITRF)核心站組建長度不同但相對位置長期不變的基線，數據采取單站模式進行相同的預處理策略，僅在誤差方程建立時分別采用非差模型與雙差模型，對連續一年的數據分別進行非差定位解算和雙差定位解算，以“相對坐標”作為比對值分析兩種模型之間實際定位精度的差異性。

1 模型比較

以無電離層組合值作為觀測值，其消除了載波和測碼偽距上的電離層一階項，電離層組合模型的非差觀測方程為：

(1)

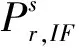
假設衛星軌道和鐘差已知，對流層延遲表示為天頂延遲和投影函數的乘積，即T=zhd×Mh(θ)+zwd×Mw(θ)，其中zhd和zwd分別為天頂流體靜力學延遲和天頂濕延遲，Mh(θ)和Mw(θ)為靜力學映射函數和濕映射函數，天頂濕延遲zwd作為參數估計，則以消電離層組合作為觀測值的非差函數模型：

(2)

雙差觀測模型通常是先在站間單差，然后選取基準星后再進行星間雙差。假設測站r1和r2同時跟蹤GPS衛星，對衛星s1、s2的載波相位和偽距無電離層組合的雙差觀測方程：

(3)

(4)

GNSS精密數據處理流程如圖1所示，包括文件讀取、數據預處理、誤差改正、參數估計與結構輸出等5個模塊。圖1中原始GNSS觀測值中包含各種誤差，只有消除或者改正誤差影響，才能實現靜態厘米級甚至毫米級的定位結果。GNSS數據處理中的誤差改正如衛星鐘差、衛星天線相位中心偏差、相位纏繞效應、衛星鐘相對論效應、接收機天線相位中心改正、天線歸心改正、地球固體潮改正、海洋負荷潮汐改正、極潮改正、地球自轉改正、對流層延遲等，一般采用數學模型或經驗公式進行改正，而接收機鐘差、對流層濕延遲等通常作為待估參數進行平差處理。非差模型與雙差模型從理論上分析是等價的[8]，但實際數據處理中，非差模型中需要詳細而準確的誤差改正方法，而雙差模型利用觀測的同步衛星通過對站、星間組差進行解算，可以消去衛星鐘差、接收機鐘差和硬件延遲小數部分，消弱或消除共性誤差項的影響。

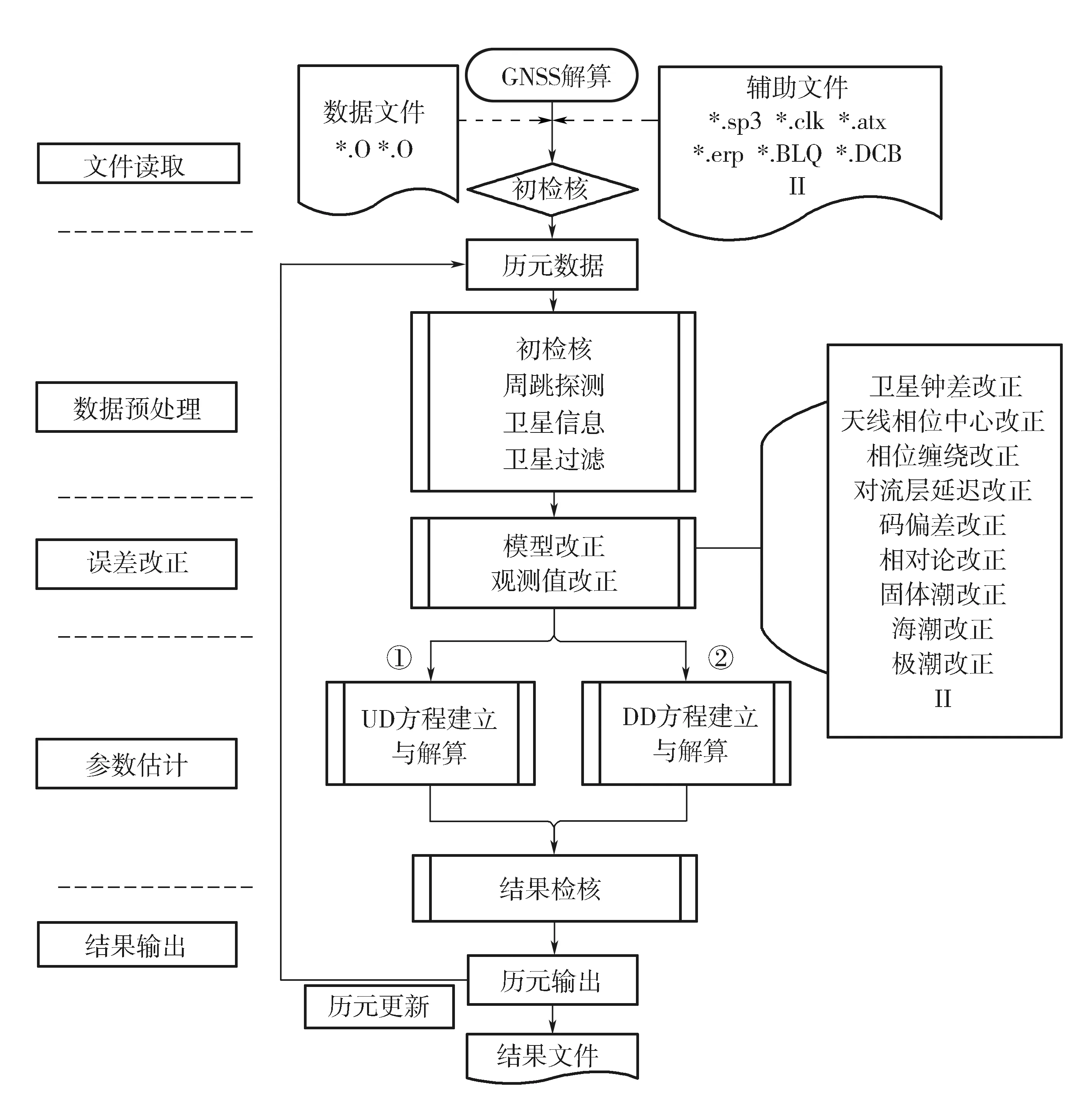
圖1 GNSS數據計算流程圖

為了比較雙差模型與非差模型實際定位結果的差異，在圖1的數據處理流程中，對兩個測站采用雙差模型或非差模型進行定位解算時，在文件讀取、數據預處理和誤差改正環節均逐測站進行，采用完全一致的精密星歷產品、周跳探測算法、誤差改正模型等，僅在參數估計環節中分別建立非差觀測方程和雙差觀測方程。由于非差模型得到的坐標參數直接是絕對坐標，而雙差基線得到的坐標參數是相對坐標，必須引入坐標基準進行基線網平差才能得到絕對坐標。如果比較絕對坐標值，則雙差模型引入基準的精度影響兩者等價性的判斷。因此，本文先對基線的兩個測站采用非差模型逐測站組建非差方程進行定位解算，得到測站坐標后反算得到兩個測站的相對坐標值，將其與雙差模型得到測站間的相對坐標值進行對比，避免基準精度對兩種模型定位精度等價性分析的影響。

2 實驗與分析

選取ITRF核心站組成長度不同但相對位置長期不變的基線，分別是STJO-STJ2、ZIMJ-WAB2、ALGO-NRC1、HERS-WSRT 4條基線(基線長度分別是42 m、5 194 m、198 574 m、487 618 m)，所選測站均是參與ITRF08框架建立的核心站(除了STJO站)，表1是從ITRF網站(itrf.ensg.ign.fr)查詢各站在2013-01-01的ITRF08框架下的坐標值和年運動速度，各基線的測站板塊運動速度基本相同，則基線的相對坐標值可認為始終保持不變，其中STJ2不在ITRF2008中，但由于與STJO站相距42 m，可認為年速率與STJO站相同。對4條基線2013年全年數據進行非差模型和雙差模型定位解算，比較雙差解與非差解的相對坐標結果的差異。由于部分測站某些天觀測數據缺失，如ZIMJ測站前120天沒有數據，本文僅對有效天數的數據進行解算。

表1 在歷元2013/01/01時ITRF2008框架下的測站坐標和速度信息

以無電離層組合值為觀測值，采用IGS發布的15 min精密星歷和5 min鐘差的最終產品改正軌道和衛星鐘差誤差，所有cm級以上的誤差均進行改正，參數與模型設置如下表2。雙差計算策略中數據預處理也是以站為單位進行單站預處理，與非差計算策略中預處理過程完全一致，兩中處理方式僅在矩陣構建和解算過程不同。為避免過度參數化，對于超短基線STJO-STJ2雙差解算時，不估計對流層濕延遲參數。

表2 參數與模型設置

圖2為非差與雙差模型計算得到的各基線在XYZ3個方向的相對坐標值，其中“DD”表示雙差模型，“UD”表示非差模型。進一步對全年的各個方向的相對坐標值序列計算其平均值和標準偏差，如表3所示。

表3 不同基線的非差與雙差解時間序列的平均值和標準差

圖2 非差與雙差解算基線的不同方向的相對坐標值分量序列

分析圖2和表3可知，非差解的全年的相對坐標時間序列標準差的均值是(5.6,4.5,5.4) mm，而雙差解是(3.4,3.1,4.0) mm，雙差模型的解算精度和穩定性整體優于非差模型。隨基線的增長，雙差模型差異呈現累積性，而非差模型差異基本沒變化，如42 m超短基線STJ2-STJO全年數據非差解和雙差解的標準差分別為(6.2,4.8,5.7) mm和(3.0,2.9,3.0) mm，而487 km長基線HERS-WSRT則是(5.7,4.5,5.4) mm和(4.7,2.8,4.7) mm。短基線情況下，雙差模型能夠有效消弱或消除觀測誤差，定位解算比非差模型更加穩定，從圖2中更能直觀看出雙差解算的坐標序列更加集中穩定。隨著基線增長，空間誤差的相關性減弱，雙差模型的偏差累加，其穩定性降低，但依然優于非差模型，如487 km的基線HERS-WSRT全年數據的非差模型的坐標序列標準差為(5.7,4.5,5.4) mm，而雙差的坐標序列標準差為(4.7,2.8,4.7) mm。

圖3 非差與雙差解算基線的相對坐標值在不同方向差值

表4 不同基線非差與雙差解的偏差平均值和標準差

進一步對4條基線的雙差與非差解算得到相對坐標值在X、Y、Z方向分別進行作差，差值如圖3所示，全年差值平均值和標準差如表4所示，非差解與雙差解在XYZ方向全年坐標分量互差的標準差均值是(5.2,4.6,4.4) mm，三維坐標偏差標準差達到8.2 mm，表明非差解與雙差解存在定位偏差，但非差與雙差模型解算結果不存在系統誤差，如STJ2-STJO偏差值的平均值為(-1.2,-2.0,0.2) mm，標準差為(4.2,4.3,3.9) mm。理想狀態下GPS的相位觀測噪聲為2～3 mm，計算的最好精度約為幾個mm，而實際數據處理中，由于誤差改正模型不精細和計算方法不完善等因素，解算結果的誤差會更大。本文所編寫的GNSS數據處理軟件[10-11](www.gnsser.com)中對定位誤差采用表2所列的模型改正方法，但對光壓模型、高階電離層改正等暫未考慮，算例中的精度并不具有普遍代表，但由于非差處理與雙差處理僅是在方程建立與參數解算設置不同，因此，算例可以反映出雙差模型在精度穩定性上比非差模型具有一定優勢，特別是短基線情況下。

3 結 論

非差解和雙差解從理論上是模型等價的GNSS數據處理方式，但實際數據處理中，誤差改正模型目前大多是采用經驗模型，而測站的環境(溫度、濕度、氣壓、板塊運動)等是動態變化的，誤差改正模型不夠精細和計算方式不夠完善等因素，導致實際解算中非差模型與雙差模型存在差異性。通過對長度不同但相對位置不變的基線一年的數據進行非差與雙差定位解算，統計分析相對坐標分量偏差序列得知，非差解與雙差解存在定位偏差，其三維坐標偏差標準差達到8.2 mm；通過對相對坐標時間序列的標準差分析表明，雙差解算的定位精度和穩定性整體優于非差解算；但隨基線的增長，特別是超過2 000 km的超長基線，雙差模型的差異呈現累積性，而非差模型的差異基本沒變化。

隨著全球連續運行參考站網布設密度加大，GNSS基準站數越來越多，即便是全球網中也很少有超長的基線，而且計算機的性能也得到飛速提升。雖然非差模式解算效率快，但需要準確的誤差改正模型，而雙差模型可以有效地削弱或消除同類誤差源。因此，在大網參考框架維持、變形監測等高精度應用領域，可優先考慮采用雙差模型進行數據解算或者以非差模型的結果作為雙差模型的先驗信息，再采用雙差模型進行聯合解算。