集大智慧，做小變式，再成大智慧
——《數列求和》教學設計與反思

湖南華容二中 胡啟軍

一、教學分析

1.教材分析。數列這一章是高中代數的重點內容之一，在歷年高考試題中占有較大的比重，題型有選擇題、填空題和解答題。本節課內容是常見的幾種數列求和方法。此內容常以解答題的形式出現。

2.學情分析。學生已復習了等差等比數列求數列的通項,對于等差等比數列的求和已經有了較好的掌握,本節課主要是針對其他的幾種特殊的數列求和。通過新舊知識的融合,將零散的知識點聯系起來，幫助學生建構數列求和的完善知識體系。

二、教學目標

通過觀察數列的通項式,根據不同數列的特征，靈活選用數列的求和方法,通過典型例題的選講,使學生能達到舉一反三,觸類旁通的目的；通過以練為主的方式,調動學生的學習積極性,樹立學生自信心；通過主動探索,合作交流,感受探索的樂趣和成功的體驗,體會數學的理性和嚴謹。

三、教學方法

通過三個問題、三組變式,滲透數列求和的四種方法；運用變式教學確保學生參與教學活動的持續熱情,培養學生思維的廣闊性、深刻性、創造性。使學生做到每做一道題,解決一種題型,復習一系列知識，掌握一兩個規律。

四、教學過程

（一）知識要點

（2）分組求和法：直接運用公式法求和有困難,若將這類數列適當拆開,可以分成幾個等差、等比或常見的數列,先運用公式法分別求和,然后再合并。

（3）倒序相加法：在數列求和中,若和式中到首尾距離相等的兩項和有其共性或數列的通項與組合數相關聯,則常可考慮選用倒序相加法,發揮其共性的作用求和（這也是等差數列求和公式的推導方法）。

（4）錯位相減法：如果數列的通項是由一個等差數列的通項與一個等比數列的通項相乘構成,那么常選用錯位相減法將其和轉化為一個新的等比數列的和，然后求解。

（5）裂項相消法：如果數列的通項可“拆成兩項差”的形式,且相鄰項分裂后相關聯,那么常選用裂項相消法求和。

（二）方法回顧

例1 （1）等差數列{an}中,an=2n-1,則數列{an}的前n項和為__________；（2）數列的前n項和為________ ；（3）數列的前n項和為______________。

歸納：數列通項an的特點。設計意圖：遇新題,憶舊題,多思考，善聯想，多變換，找規律；既加大課堂容量,又培養學生的應變能力和創造性思維能力。

歸納：數列通項an的特點。

設計意圖：通過例題所提供的結構特點,鼓勵、引導學生大膽地猜想,以培養學生的發散思維。

設計意圖：通過一題多思,一題多變，橫向聯想,不僅提高學生運用所學知識解決數學問題的能力,而且發展學生的求異思維。

歸納推廣：若數列｛an｝為等差數列，公差為d,則=____________________。

設計意圖：有目的、有意識地引導學生從“變”的現象中發現“不變”的本質,從“不變”的本質中探究“變”的規律，可以幫助學生使所學的知識點融會貫通。

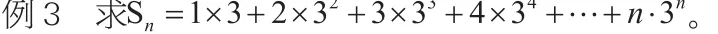
歸納：數列通項an的特點。

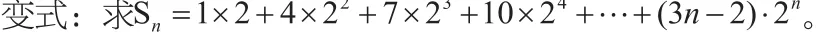
設計意圖：根據學生的實際，適當降低錯位相減法的難度要求,關注學生的數學學習情感,樹立學生自信心,提高學習興趣、激發學習動機。

小結：數列求和的方法包括：（1）公式法；（2）分組求和法；（3）裂項相消法；（4）錯位相減法。

設計意圖：引導學生歸納數列求和的方法及通項特點,使學生明確了本節課的學習目的,又實現了自我反饋。

（三）鞏固演練

1.已知數列{an}是等差數列,且是數列{an}的前n項和。（1）求數列{an}的通項公式an及前n項和Sn；（2）若數列{}滿足，且Tn是數列{}的前n項和，求與 Tn；（3）若，求數列｛Kn｝的前n項和。

2.設數列{an}的前n項和為Sn,且為等差數列,且（1）求數列{an}和{}通項公式；（2）設，求數列{cn}的前n項和Tn。

五、反思與評析

1.反思。變式教學在課堂上展示知識發生、發展、形成的完整認知過程,形成“問題、變式、反思、體驗”教學模式,讓學生在無窮的變化中體會學習數學的快樂,有利于培養學生探索問題的能力。

2.評析。張景中數學家提出“改造數學使之更適宜于教學和學習,是教育數學為自己提出的任務。”本節課教學設計通過一題多思、一題多變、橫向聯想,不僅提高了學生運用所學知識解決數學問題的能力,而且發展了學生的求異思維；有目的、有意識地引導學生從“變”的現象中發現“不變”的本質,從“不變”的本質中探究“變”的規律,可以幫助學生使所學的知識點融會貫通。