邊條件含譜參數有理式的Sturm-Liouville問題的譜不等式

傅守忠，王 忠

（肇慶學院 數學與統計學院，廣東 肇慶 526061）

0 引言

起源于求解熱傳導方程的Sturm-Liouville(以下簡稱S-L)問題是指S-L方程

賦予分離的自伴邊條件

所形成的特征值問題,其中1/p,q,w都是[a,b]上的可積實值函數,且p和w幾乎處處為正,h和H為實數或∞,其中∞代表對應的端點為Dirichlet的邊條件,例如H=∞表示y(b)=0.S-L問題已成為數學物理許多應用領域(如振動力學和量子力學等)的重要理論工具.在由彈簧連接的振動系統中,將一端完全固定,振動方程分離變量后,形成的S-L問題在該端取Dirichlet邊條件y(·)=0.若一端固定在1個彈性支承上(比如該端可在與彈簧振動方向垂直的光滑的桿上滑動),則對應的邊條件為一般邊條件(2).熟知,經過經典的Liouville變換,可將S-L問題(1)～(2)規范化為[0,1]區間上等譜的勢方程S-L問題∶

經典S-L問題(3)～(5)誘導出Hilbert空間L2[0,1]中定義的常微分算子L的譜問題Ly=λy(參見文獻[1-3]),其中算子L及其定義域為

若振動系統中彈簧的一端相對固定,而另一端懸掛1個擺動的物體,則其振動方程分離變量產生的S-L問題的邊條件就與系統的振動頻率(即譜)相關,即h和(或)H依賴于λ.還有很多物理問題的數學模型會轉化為邊條件含譜參數的S-L問題[4].多年來,許多學者致力于這類問題的研究,得到很多有意義的成果.諸如將問題納入一種特定的Hilbert空間后,誘導出的微分算子是自伴的,譜由特征值組成,特征函數系是完備的,等等[5-8].

賦予不同邊條件的S-L問題特征值間的不等式不僅有趣,而且在特征值分布、近似計算及確定給定特征值的序號等問題中有重要的應用價值.例如由方程(3)～(5)組成的S-L問題的特征值遞增序列,與方程(3)賦予邊條件(4)和Dirichlet邊條件y(1)=0生成另一個S-L問題的特征值遞增序列之間,存在交錯不等式,由此及Sturm比較定理和的信息(如所對應的特征函數的零點個數),就可以得到對應于一般S-L問題的特征值的相應信息[9-10].利用Weyl-Titchmarshm-函數及其性質[11-12],文獻[13]和[14]給出端點x=1處的邊條件依賴于aλ+b或其倒數的S-L問題的特征值與間的交錯不等式.

本文中,筆者討論邊條件依賴于特征參數分式線性函數的S-L問題的相應結論,即邊條件(5)變成

的S-L問題,其中a≠0,b,c≠0,d為實數,且滿足ad-bc＞0(這里a=0和c=0的情形可分別化歸成文獻[13]和[14]中的結論).文獻[15]已經證明這類問題誘導出的S-L算子是自伴的,因而其特征值都是實的.

本文將利用由(3),(4)和(6)(簡寫為(3)-(4)-(6))組成的S-L問題的Weyl-Titchmarshm-函數及其性質,給出該問題的廣義特征函數,并得到其特征值遞增序列與序列間的交替不等式,最后得到這2組特征值可以唯一確定勢函數q(x).

1 Weyl-Titchmarshm-函數及其性質

對任意的復數λ,設v(x,λ)是方程(3)滿足初始條件y(0)=1,y′(0)=h的解(對應于h=∞即邊條件y(0)=0,初始條件改為y(0)=0,y′(0)=1),則對任意的λ,函數v(x,λ)都滿足方程(3)和邊條件(4),且由常微分方程的解對其參數的連續依賴性,v(x,λ)及v′(x,λ)都是λ的整函數.

定義Weyl-Titchmarshm-函數[11-12]

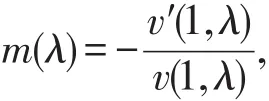
則m(λ)是λ的半純函數,且m(λ)的極點集合恰好是

引理1[13]當時,

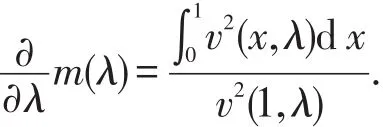
推論1[13]對每個自然數

引理2[12,16]m(λ)有如下漸近式

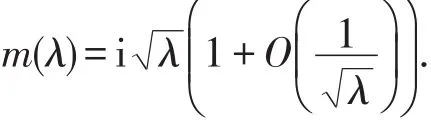
特別地,當λ→-∞ (沿實軸)時

推論2[13]若記則m(λ)在區間內由-∞連續地嚴格遞增到+∞.

引理3λ?是由方程(3),(4)和(6)生成的S-L問題的特征值當且僅當等式包含∞=∞的情形，但不用區分±∞.

證 由v(x,λ)所滿足的條件和m(λ)的定義,經簡單變形可知必要性成立.

在將∞-∞定義為0的意義下,由引理3易見,方程(3),(4)和(6)生成的S-L問題的廣義特征函數為

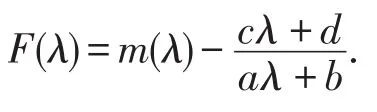
顯然F(λ)的極點恰好是

2 主要結論與證明

定理1設S-L問題(3)-(4)-(6)的特征值遞增序列為

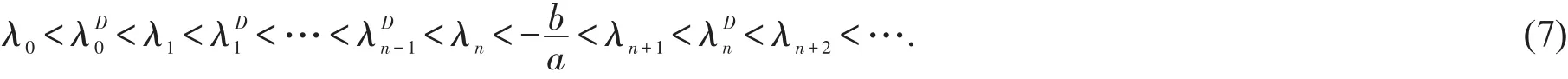
2)若存在非負整數n,使得則

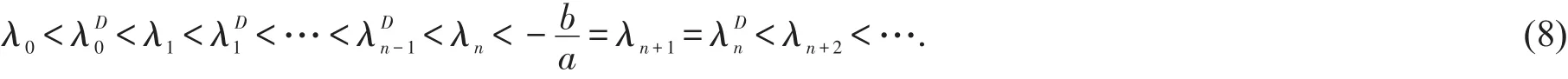
證 1)由推論2,m-函數m(λ)在區間內都連續,故F(λ)在區間

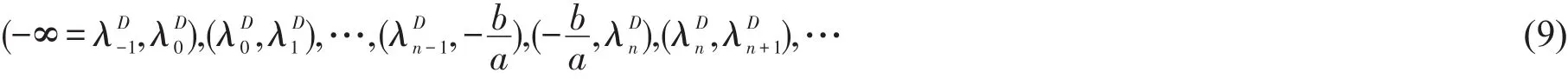
內也都連續.又由于a≠0且ad-bc＞0,故

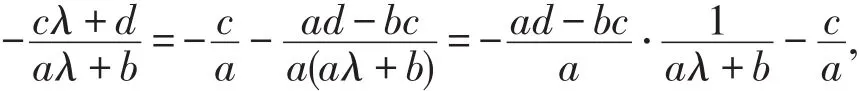
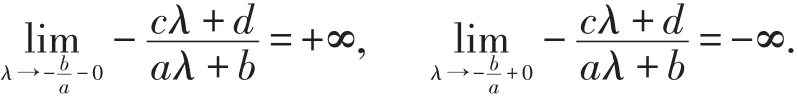
再根據推論2,F(λ)在公式(9)所列的各區間內都由-∞連續地嚴格遞增到+∞,故由連續函數的介值定理知F(λ)在上述每個區間內都有且只有1個零點.結合引理3知F(λ)的零點恰好都是由方程(3)-(4)-(6)生成的S-L問題的特征值,即得不等式(7).

注 事實上,F(λ)的零點就是λ的函數m(λ)與的交點,圖1給出定理1中的不等式的幾何意義.

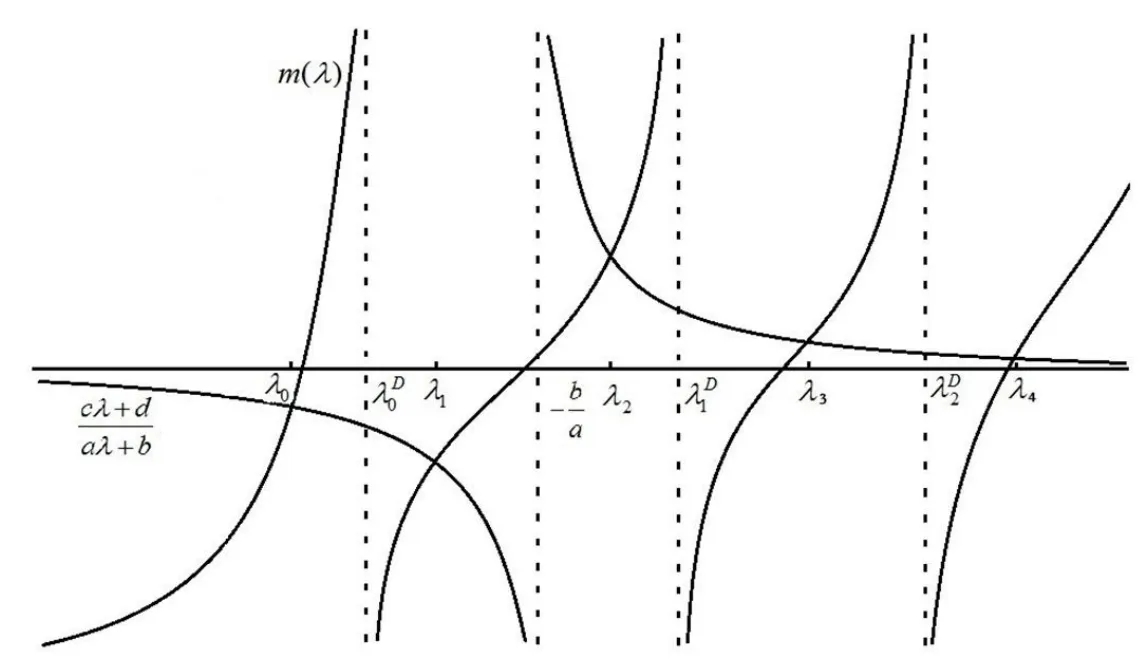
圖1 特征值不等式的幾何意義

定理2 對固定的h及滿足ad-bc＞0及a≠0,c≠0的實數a,b,c,d,S-L問題(3)-(4)-(6)的特征值和將邊條件(6)換成Dirichlet邊條件y(1)=0的S-L問題的特征值可唯一確定q(x).

證明方法類似文獻[13]中定理2的證明.