函數與導數的綜合應用測試題（A 卷）參考答案

一、選擇題

1.C 2.A 3.D 4.B 5.A 6.B

7.B 8.D 9.D 1 0.B 1 1.A 1 2.B

二、填空題

1 3.(—∞，1] 1 4.(—∞，—3]

三、解答題

1 7.f "(x)=3x2+2(1—a)x—a(a+2)。

(2)因為曲線y=f(x)存在兩條垂直于y軸的切線，所以關于x的方程f "(x)=3x2+2(1—a)x—a(a+2)=0有兩個不相等的實數根。所以Δ=4(1—a)2+1 2a(a+2)＞0，即4a2+4a+1＞0，所以a≠—所以a的取值范圍為

1 8.(1)當a=—1時，f(x)=—l nx+x2+3，定義域為 （0 ，+∞），則f "(x)=+x。由得0＜x＜1。所以函數f(x)的單調遞減區間為(0，1)。

(2)因為函數f(x)在區間(0，+∞)上是增函數，所以f "(x)=+x+a+1≥0在(0，+∞)上恒成立，所以x2+(a+1)x+a≥0，即(x+1)(x+a)≥0在(0，+∞)上恒成立。

因為x+1＞0，所以x+a≥0對x∈(0，+∞)恒成立，所以a≥0，故實數a的取值范圍是[0，+∞)。

1 9.(1)因為f(x)是二次函數且關于x的不等式f(x)≤0的解集為{x|—1≤x≤3，x∈R}，所以設f(x)=a(x+1)(x—3)=a x2—2a x—3a(a＞0)。

因為f(x)min=f(1)=—4a=—4，所以a=1，故函數f(x)的解析式為f(x)=x2—2x—3。

(2)因為g(x)=0)，所 以g "(x)=1+

令g "(x)=0得x=1或x=3。

當x變化時，g "(x)，g(x)的取值變化情況如表1：

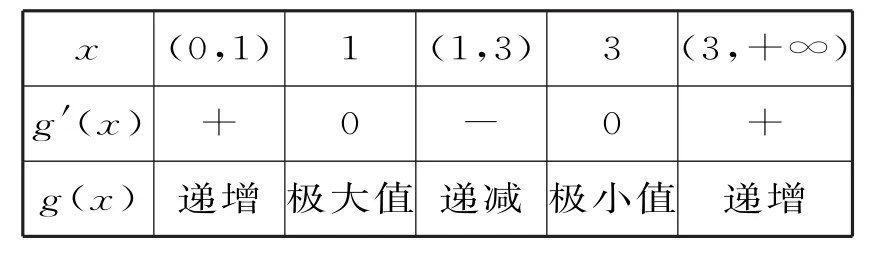
表1

當0＜x≤3時，g(x)≤g(1)=—4＜0。又因為g(x)在(3，+∞)上單調遞增，且—2 0—2＞25—1—2 2=9＞0，其中e5＞3，因而g(x)在(3，+∞)上只有1個零點。故g(x)在(0，+∞)上僅有1個零點。

2 0.(1)由已知得f "(x)=1)，則f "(1)=0。

而f(1)=l n1+所以曲線y=f(x)在x=1處的切線方程為

由f "(x)=0，得0＜x＜或x＞1；

由f "(x)=0，得

所以f(x)的單調遞增區間為和(1，+∞)，f(x)的單調遞減區間為

設h(x)=，則h "(x)=

由h "(x)＞0得，所以h(x)在上單調遞增；

由h "(x)＜0得，所以h(x)在，+∞）上單調遞減。

所以h(x)的最大值為，所以，故

從而實數a的取值范圍為

2 1.(1)函數f(x)的定義域為(—∞，+∞)，且a≤0，f "(x)=2 e2x—aex—a2=(2 ex+a)(ex—a)。

①若a=0，則f(x)=e2x在(—∞，+∞)上單調遞增。

②若a＜0，由f "(x)=0，得x=

故f(x)在上單調遞減，在上單調遞增。

(2)①若a=0，則f(x)=e2x≥0恒成立。

②若a＜0，則由(1)得，當x=時，f(x)取得最小值，最小值為

綜上可知，實數a的取值范圍是

2 2.(1)由f(x)=l nx得f "(x)=，函數f(x)的圖像在點(1，f(1))處的切線的斜率為f "(1)=1，切線方程為y—0=x—1，即y=x—1。由已知得它與g(x)的圖像相切，將y=x—1代入得x—1=x2—b x，即x2—(b+1)x+1=0，所以Δ=(b+1)2—2=0。解得b=±—1，即實數b的值為±—1。

(2)h(x)=f(x)+g(x)=l nx+—b x，所以h "(x)=

根據函數h(x)在定義域(0，+∞)上存在單調減區間，所以?x＞0，使得b＜0，即b＞x+，由于當x＞0時x≥2，所以b＞2。所以實數b的取值范圍(2，+∞)。

(3)對于區間[1，2]上的任意實數x，有［1—b，2—b］。要使得對于區間[1，2]上的任意兩個不相等的實數x1，x2，都有|f(x1)—f(x2)|＞|g(x1)—g(x2)|成立，f(x)是增函數，不妨設x1＞x2，則f(x1)＞f(x2)，問題|f(x1)—f(x2)|＞|g(x1)—g(x2)|，等價于—f(x1)+f(x2)＜g(x1)—g(x2)＜f(x1)—f(x2)，從而f(x1)—g(x1)＞f(x2)—g(x2)，且f(x1)+g(x1)＞f(x2)+g(x2)，即f(x)—g(x)與f(x)+g(x)都是增函數。又導數的幾何意義是切線的斜率，得到|f "(x)|＞|g "(x)|，即＞|b—x|，于是，即，所以≤b≤2，即b的取值范圍為