一種無后坐炮渦輪尾翼彈轉速分析

張陳曦,何 永,吳勝權,周君濤,蔣瀟蓉,郁家耀

(南京理工大學 機械工程學院， 南京 210094)

無后坐炮是一種特殊火炮，利用射擊過程中火藥燃氣經炮尾噴管的反作用來消除炮身的后坐，是一種良好的單兵作戰武器。李春雷等[1]介紹了瑞典古斯塔夫無后坐炮彈藥的結構原理和性能特點；肖劍等[2]對古斯塔夫無后坐炮幾種彈藥引信做了詳細比較；吳勝權等[3]基于混合裝藥建立了無后坐炮的內彈道模型并對內彈道性能進行測試。

本文研究的是某滑膛式無后坐炮的彈丸轉速。在使用如增程破甲彈這種發射速度較高的彈丸時，為滿足彈丸飛行穩定性要求，常使用張開式的尾翼結構[4]。為使折疊的尾翼在出炮口后張開到位，需對彈丸附加一定的轉速。渦輪尾翼彈彈尾處的渦輪可以利用無后坐炮后噴氣體的作用力，賦予彈丸相對膛線炮較低的轉速，既使尾翼受轉動的離心力張開，又增強了彈丸的破甲傷害。故需對彈丸轉速規律進行分析，優化彈丸轉速。

1 無后坐炮內彈道模型

假設火藥燃燒服從幾何燃燒定律；火藥的燃燒速度與壓力成指數函數關系；膛壓采用平均壓力；在射擊起始階段，噴口打開壓力和彈丸的起動壓力相等；在射擊過程中沒有未燃完的火藥隨火藥氣體從噴口噴出；在整個射擊過程，火藥氣體的成分始終保持不變。

基于以上假設，本文研究的無后坐炮內彈道方程組共包括幾何燃燒定律、燃燒速度方程、彈丸運動方程、彈丸行程方程、氣體流量方程、氣體狀態方程和能量平衡方程[5-7]，表達式為：

(1)

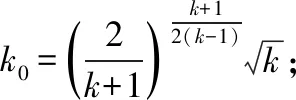
式(1)中：ψ為火藥已燃百分比；χ和ζ為火藥的形狀特征量；z為火藥相對已燃厚度；e1為火藥弧厚的一半；u1為火藥燃速系數；P為內膛的平均壓力；v為彈丸運動速度；m為彈丸質量；S為無后坐炮內膛面積；φ1為彈丸運動的次要功系數；ξ為彈丸行程；η為相對氣體流出量；φ2為消耗系數；Sj為噴管喉部面積；a為裝藥總質量；τ為相對溫度；k為絕熱指數，θ=k-1；σ為火藥力；ξ0為藥室容積縮頸長；Δ為裝填密度；ρ0為火藥密度；Vα為火藥氣體余容。

2 渦輪尾翼彈轉速的推導

2.1 渦輪尾翼彈

滑膛式無后坐炮使用的渦輪張開式尾翼彈由戰斗部、尾桿、尾翼片和渦輪等部件組成(見圖1)。渦輪是有數片(常為4片)斜置葉片的輪狀零件，如圖2所示。彈丸尾桿上的尾翼片平時合攏在尾桿翼槽內，當無后坐炮發射時，膛內的火藥氣體一邊推動彈丸前進，一邊向后噴流。此時，后噴的火藥氣體作用在彈丸尾桿的渦輪上，使彈丸產生旋轉。當彈丸飛出炮口后，尾翼在彈丸自轉的離心力作用下張開[8]，提升了彈丸的飛行穩定性。

圖1 渦輪張開式尾翼彈簡圖

2.2 庫塔-儒可夫斯基公式的運用

本文研究的彈的渦輪轉速問題與汽輪機的葉片工作原理類似，彈尾部的4片渦輪葉片按一定間距排列構成葉柵，受流體作用下產生運動。假設身管內氣體為理想氣體，氣流不可壓縮，且處于一元連續的無旋定常流動，葉片上下表面的膛壓相互抵消對渦輪旋轉運動不起作用。現建立直角坐標系O-xy，葉柵的結構和流動參數等如圖3所示。葉片長度為b；葉片與水平面夾角為β；葉片間距稱為柵距，用L表示。

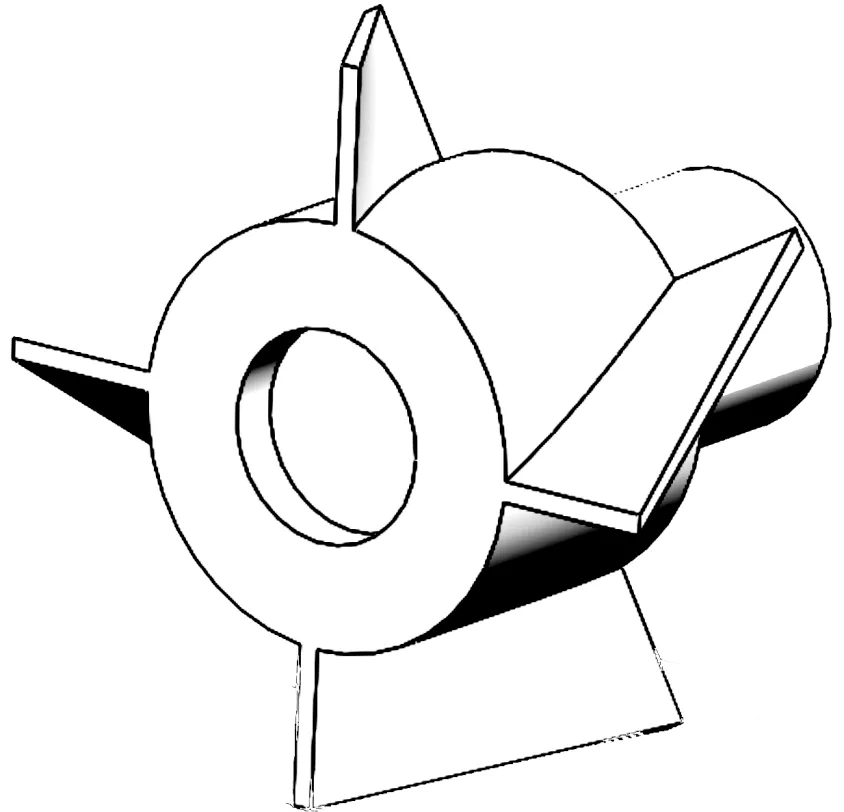
圖2 渦輪結構

圖3中虛線框ABCDA為葉柵的流場控制面，線段AB與CD平行于y軸，其長度為L，且遠離葉柵。取控制體內平均密度為ρ。假設每條線段上流體的速度與壓強都是各自均等的，AB上流體受壓強為P1，其速度為v1、方向水平靠近葉柵；CD上流體受壓強為P2、其速度為v2、方向與葉柵平行遠離葉柵，且v2x=v2cosβ、v2y=v2sinβ。AD、CB為相平行的流線，各對應點上的壓強分布完全相同，故可不考慮其對控制體內流體的影響。設控制體內流體對單位高度葉片的合力為F，其關于坐標軸的投影為Fx、Fy。

圖3 渦輪兩側的流動參數分布

根據葉柵的庫塔-儒可夫斯基公式[9]的推導過程，考慮到流體流動的慣性力比重力大得多，可忽略重力的影響，故由連續性方程可得

v1L=v2xL

(2)

由動量方程可得

(3)

由伯努利方程可得

(4)

聯立式(2)、式(3)、式(4)可求得作用在渦輪上的阻力Fx和作用在渦輪上的升力Fy。

(5)

由式(5)可知，若得到控制體內平均密度ρ與AB上流體的速度v1，即可得到作用在單位高度葉片上的升力Fy，進而可求得作用在渦輪上的總轉矩大小。

2.3 無后坐炮膛內氣流參數分析

無后坐炮彈丸發射過程中，彈后空間可看作是半封閉的。假設在彈道周期內，膛內同時存在的氣、固二相混合流動看成單一的火藥燃氣的流動，且認為火藥燃氣在膛內是均勻分布的。通過運用基于比例膨脹假說的半封閉彈道原理，得出單元火藥氣體沿彈后空間長度向的速度與加速度成直線分布的規律[10]。如圖4所示，沿膛底與彈丸中軸線建立直角坐標系O’-xvx，x為彈后空間內任意具有速度vx的火藥氣體單元坐標；x=0時為膛底，此時膛底火藥氣體單元速度為-vkh；l為半封閉彈后空間的長度，當x=l時彈底火藥氣體單元速度即為彈丸速度v。由此可得到此種在彈后至膛底任意位置處的單元火藥氣體其x向速度vx的表達式：

(6)

圖4 彈后空間內氣體速度分布

為了得到vkh的變化規律，由文獻[10]中列出以下方程組：

(7)

其中：g為當地重力加速度；Skh、Skp為膛底與彈后任意臨界斷面的面積；Pkh、Pkp為膛底與彈后任意臨界斷面的壓力；j為彈后空間內氣體及燃燒藥粒的質量，j=a(1-η)；δ0為彈后空間的平均密度，δ0=j/(STl-VT)，其中ST為彈后空間的截面積，VT為彈后尾桿、尾翼、渦輪的總體積；wkh取彈后空間的平均比容，wkh=1/δ0；

方程組(7)可求出兩個vkh值。由于彈丸速度v在圖4坐標系O’-xvx下始終大于等于0，而膛底火藥氣體的速度矢量在此坐標系下一定小于等于0，故式(6)中默認vkh的值大于等于0，故式(7)的vkh解取非負數，膛底實際氣流速度應為-vkh。將vkh代入式(6)中即可得到符合坐標系O’-xvx的彈后空間內任意位置處的單元火藥氣體x向速度。

2.4 彈丸轉速公式

流經彈后渦輪的氣流速度應由兩部分組成，其一為2.3節中介紹的火藥燃燒在膛內形成的氣流，其二為彈丸運動引起的氣體相對渦輪運動的氣流。設渦輪的前端至膛底距離為x1(如圖4所示)，由式(6)可得到渦輪前端火藥氣流速度為vx1，彈丸運動引起的相對渦輪運動的氣體速度為-v，此時式(5)中應有ρ=δ0，v1=vx1-v，故有

Fy=δ0(vx1-v)2Ltanβ

彈后渦輪可簡化為如圖5所示渦輪結構視圖。葉片單元離渦輪軸心距離為r，葉片底端距軸心r1，葉片頂端距軸心r2。

故單個葉片受總力距為

由圖5知，L=(2πr)/4，由此得渦輪受總力矩為

圖5 由彈底向彈頂的渦輪視圖

由動量距定理，設彈丸關于x軸(如圖4)的轉動慣量為I，彈丸角速度為ω，忽略彈丸定心部與身管轉動接觸的摩擦力矩，則有彈丸受轉動力矩M為

即

(8)

對式(8)左端關于0～ω進行積分、右端關于0～t進行積分，則有

則彈丸每分鐘轉速N可表示為

(9)

由式(1)、式(6)、式(7)可求得v、vx1、δ0的一系列關于時間t的數值解，對式(9)應用數值積分法可最終求解得彈丸轉速N。

3 彈丸轉速的仿真與分析

本研究以某無后坐炮為例，其口徑為82 mm。渦輪尾翼彈的葉片長度b為15 mm，葉片內徑2r1為38 mm，外徑2r2為72 mm。依據第1、2小節列出的公式，并利用軟件Matlab進行數值求解[11]，可得到式(9)中的彈丸每分鐘轉速N。

圖6為渦輪葉片與水平面夾角β為30°與33°時彈丸轉速隨時間變化規律，圖7為兩種葉片角度彈丸的角加速度α，圖8為身管膛內平均壓力值隨時間的變化規律，圖9為未考慮彈丸運動影響的渦輪前火藥氣體單元速度vx1、考慮彈丸運動影響的渦輪前火藥氣體單元速度v1、膛底火藥氣體單元速度vkh。

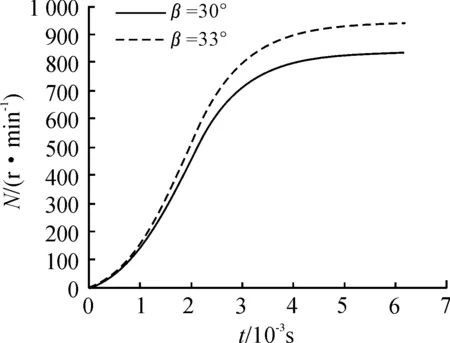
圖6 彈丸在不同葉片角度下的轉速

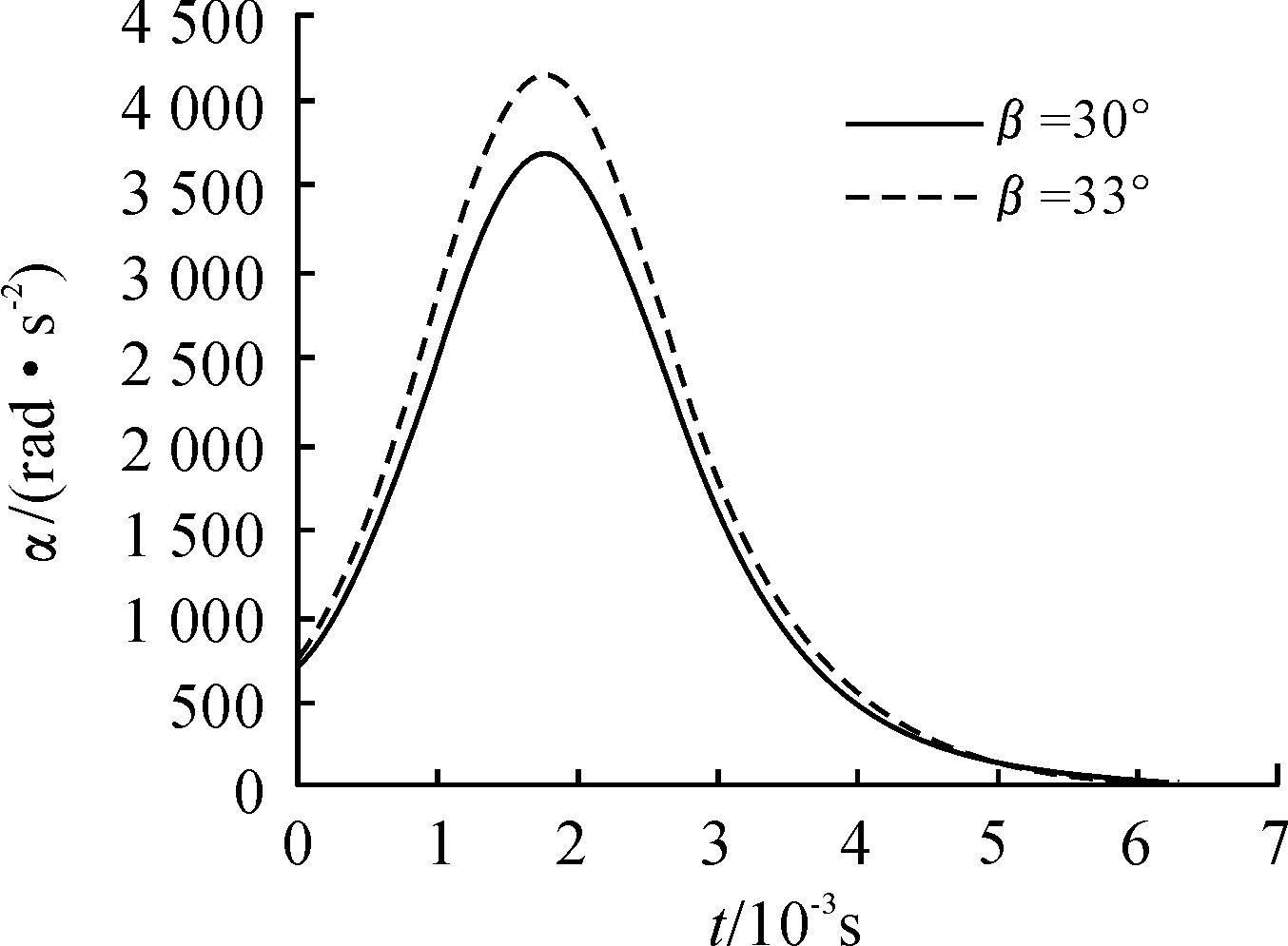
圖7 彈丸在不同葉片角度下的轉速的角加速度

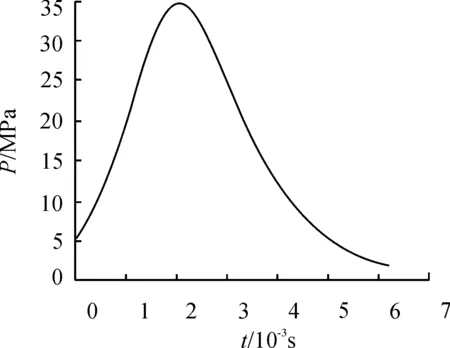
圖8 彈后平均壓力變化

圖9 氣體單元速度比較

從圖6中可以看出，彈丸轉速隨時間逐漸增加，彈丸在整個膛內運動階段葉片β角大的其角速度相對大。計算的彈丸出炮口轉速與實驗數據結果如表1所示，實驗結果與數值計算值較為接近。

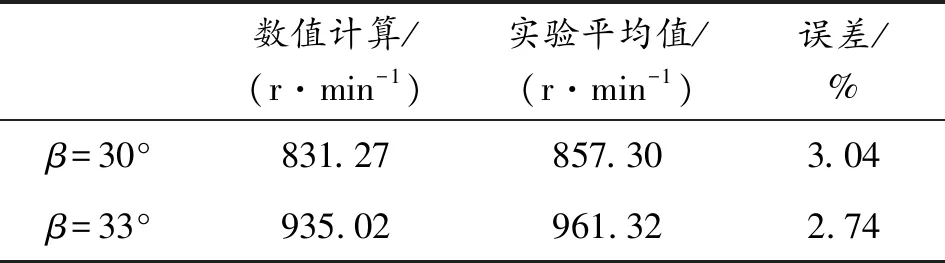
表1 計算的彈丸出炮口轉速與實驗結果

工程實踐中，此種渦輪尾翼彈的轉速在800～1 000 r/min時，既能保證尾翼順利張開，也保證了彈丸的破甲傷害。在此轉速范圍內，渦輪葉片的角度由式(9)可逆推得到設計為29.1～34.7°較為合理。

圖7所示的彈丸的角加速度先增大后減小直至區域平緩，在2 ms附近，彈丸達到最大角加速度，這與圖8所示的膛壓達到最大值的時間較為接近。由圖9可知作用在渦輪上的氣流始終沿圖4坐標系負x向流動，氣流速度變化率先增大后減小，亦與圖6所示彈丸轉速變化相符。

4 結論

所得數值計算結果與實驗測得轉速較為接近，可為按轉速要求設計渦輪尾翼彈進一步優化彈丸轉速提供依據。