轉子不對中非線性動力學特性研究
馬文生,李方忠,陳平偉,李長波,李忠剛
(1.重慶水泵廠有限責任公司總經辦, 重慶 400033; 2.重慶機集團博士后科研工作站,重慶 400033;3.北京化工大學 機電工程學院, 北京 100029; 4.哈爾濱工業大學機電工程學院, 哈爾濱 150001)
據有關資料統計表明,約60%的旋轉機械振動故障由軸系不對中引起或與之相關[1-6]。隨著科學技術的進步和工業不斷發展,旋轉機械朝著大功率、高轉速、高精度、高溫和重載的方向發展,由于這些特殊工作環境,對聯軸器的功能與作用提出了更新、更高的要求,除了連接兩個軸段,傳遞扭矩和動力外,有時還要求其具有補償兩軸段的相對偏移,起到減振、緩沖的作用,不僅要求提高傳動精度及效率,而且要求降低噪聲,達到節能的目的,還要優化轉子系統工作性能。當連聯軸器發生不對中故障時,轉子容易發生如下故障:振動過大、軸變形、油膜振蕩和軸承損壞等,對轉子系統危害較大。隨著旋轉機械的設計規范和設計要求的提高,轉子和靜子之間的間隙也逐漸變小,聯軸器-轉子系統發生不對中故障時,聯軸器-轉子系統受到的影響也較大[7-13]。
1 不對中力學模型建立
齒式聯軸器可以由左套齒和右套齒組成,左半套齒聯軸器和右半套齒聯軸器設計軸心線和連個套齒的軸心線重合時,轉子系統對中較好,這是轉子系統軸向不對中力較小,進而不考慮轉子的軸向振動,并且齒式聯軸器可以對軸向位移進行補償,可以假設這種情況聯軸器-轉子系統是對中的。當左半套齒聯軸器和右半套齒聯軸器設計軸心線和連個套齒的軸心線不重合時,此時聯軸器-轉子系統有一定的徑向不對中量,如圖1所示,本文模型只有研究平行不對中引起的非線性動力學問題。
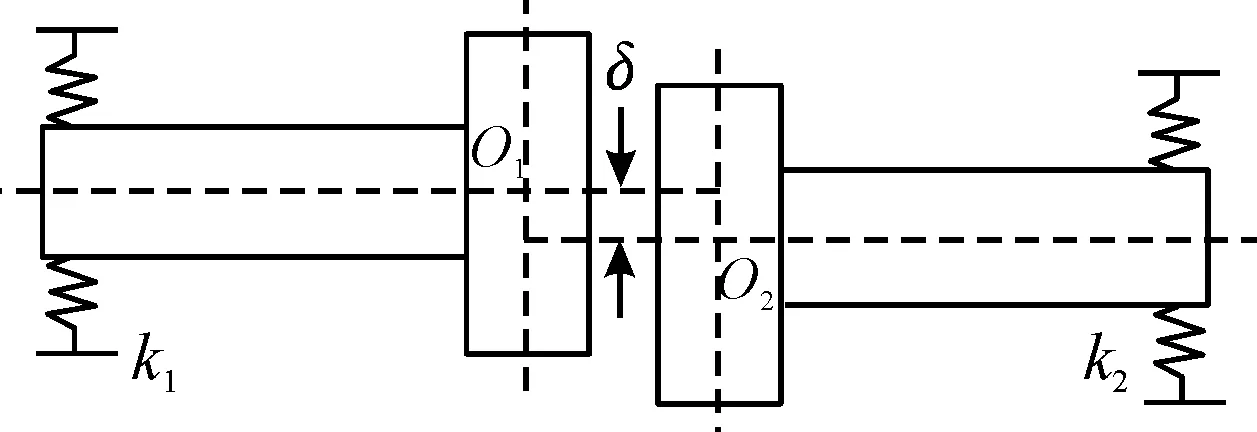
圖1 聯軸器平行不對中
建立具有聯軸器的轉子系統動力學方程,需要確定聯軸器的模型,簡化后聯軸器模型如圖1所示。聯軸器轉子系統采用有限元梁單元建模,首先把聯軸器-轉子系統系統分為若干個節點,每個節點之間采用軸段連接到一起,將軸段和結點分別建立相對應的方程,匯總所有軸段和節點的方程,最終得到整個轉子系統的動力學方程。通過選取支承處到聯軸器的軸段,并對該部分的齒式聯軸器進行等效處理,將左半套齒聯軸器和右半套齒聯軸器等效為左、右兩個節點,假設等效后的左右半套齒聯軸器的兩個節點為O1和O2,將左、右半聯軸器的質量集中到假設的左右半聯軸器的兩個節點上。由于支承處到聯軸器的軸段距離較短,可以認為是剛性軸段,此時左、右兩個半聯軸器作柱形渦動。轉子系統兩端支承假設采用彈性支承,其剛度分別取k1和k2。假設聯軸器引起的不對中量為δ,在聯軸-轉子系統高速運轉時,齒式聯軸器具有一定限位功能,假設左、右兩個半聯軸器在高速運轉過程中,一直保持著不對中量δ。
1.1 聯軸器-轉子系統的能量方程
1.1.1 聯軸器轉子系統的系統動能
左、右兩個齒式半聯軸器的型心坐標是O1(x1,y1)和O2(x2,y2)如圖2所示,左邊齒式半聯軸器存在著一定偏心量e,而右側齒式半聯軸器偏心量為0。假設聯軸器-轉子系統的轉動角速度為Ω,初相位為0,左半聯軸器的質心為C1,右半聯軸器的型心與質心重合,質心坐標向量分別為:
(1)
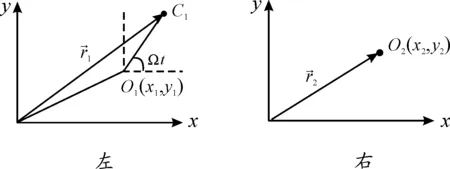
圖2 半齒聯軸器截面坐標
(2)
故系統的動能為:
(3)
在上式中,左邊聯軸器在節點處的等效質量為m1,右半聯軸器在節點處的等效質量為m2,左半聯軸器的轉動慣量為J1,右半聯軸器的轉動慣量為J2,對時間t求導為“·”。
兩個半聯軸器在運轉過程中,一直保持著固定的不對中量δ,故兩個半聯軸器之間滿足約束方程:
(x1-x2)2+(y1-y2)2=δ2
(4)
將型心O2投影到型心O1的平面上,將型心O2的坐標用型心O1的坐標表示,由式(4)得到
(5)
以坐標平面上的型心O1中心,建立相應的動坐標系η、ξ,建立的動坐標系以轉子系統的運轉角速度Ω圍繞著對應的固定坐標系x、y轉動,其運轉方式如圖3所示,得到φ=Ωt+θ,故用x1、y1和θ表示的O2的坐標位置:
(6)
將式(5)代入到式(6)得到系統的動能表達式:
(7)

圖3 聯軸器型心運轉方式
1.1.2 聯軸器-轉子系統的勢能
齒式聯軸器和軸段為剛性連接,進而不考慮不考慮其重力勢能以及彈性勢能,假設聯軸器-轉子系統兩端的支承為彈性支承,其間的軸段運動形式為柱形渦動,獲得聯軸器的型位移和支承的徑向位移具有相同的方向和大小,U表示聯軸器-轉子系統德勢能,聯軸器-轉子系統的勢能只有支承位置的彈性勢能,其勢能為:
(y1-δsin(Ωt+θ)2]
(8)
1.1.3 系統的耗散能
系統的能量耗散可以用Rayleigh耗散函數ψp表示:
(9)
在式中,左齒式半聯軸器的黏性阻尼系數為c1,右齒式半聯軸器的黏性阻尼系數為c2。
將式(5)代入式(9)得到O1的坐標和θ表示Rayleigh耗散函數ψp:
(10)
1.2 不對中動力學方程
運用拉格朗日方程,考慮系統存在不平衡力,由此得到系統的動力學微分方程組:

(11)

(12)
由z=A-1F可以得到方程:
(13)
聯軸器的結構通常為對稱式,假設質量m1=m2=m,左半齒半聯軸器剛度等于右半齒聯軸器的剛度,令k1=k2=k,假設左半齒聯軸器存在一定阻尼,而右半齒聯軸器不存在黏性阻尼,c2=0,c1=c,令x1=x、y1=y。獲得式(13),得:
(14)
對聯軸器的動力學方程進行無量綱化處理,令X=x/δ、Y=y/δ、τ=Ωt,式(14)化為:
(15)
式中,X′、X″、Y′、Y″、θ′、θ″分別表示對τ的一階、二階導數。
2 不對中和不平衡對系統響應的影響
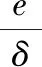
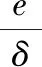

圖時X響應圖
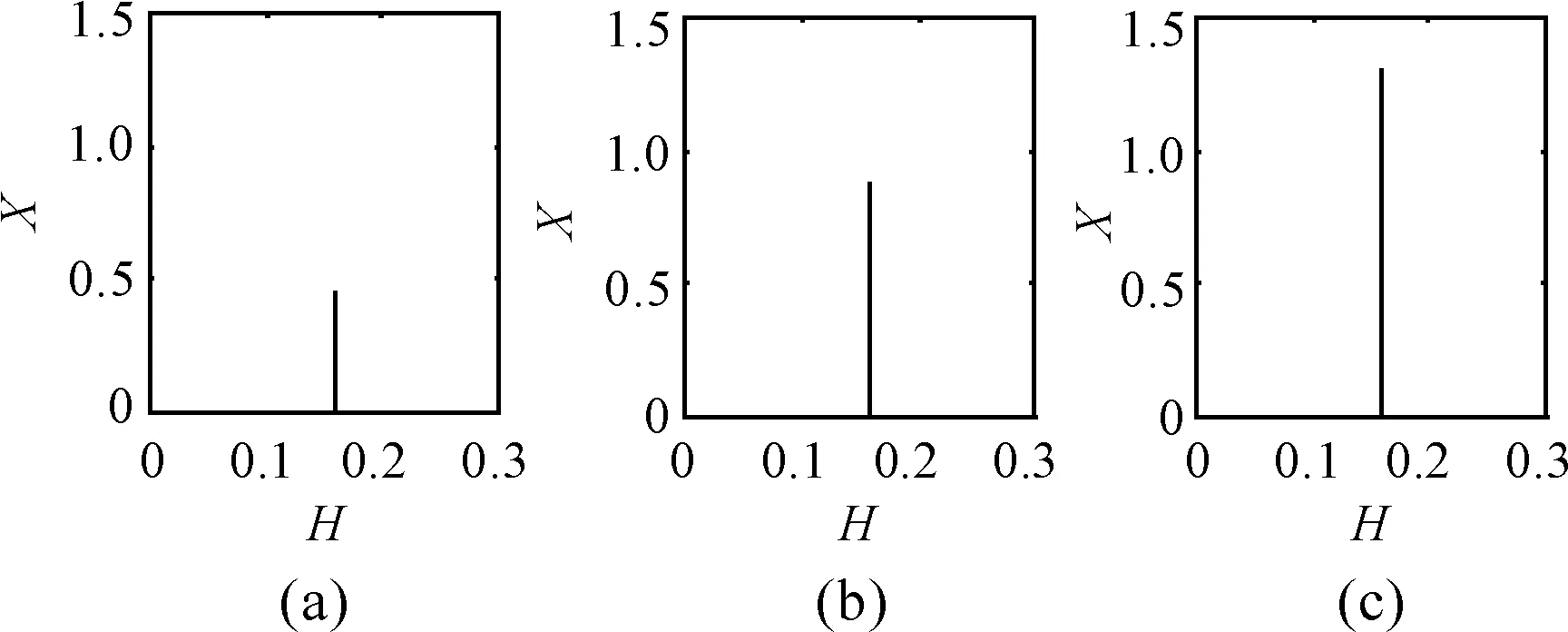
圖5 X的幅值譜圖
3 結論
帶有聯軸器的轉子系統在低轉速運轉,轉子系統不平衡量激起的不平衡力和不對中激起的不對中力共同作用于轉子系統,其運動形式為擬周期運動,轉子不平衡量引起的激勵力隨轉速增大而增大,而不對中激起的不對中力影響逐漸變小,聯軸器-轉子系統變為以基本為主的單周期運動形式。聯軸器-轉子系統的響應也與不平衡量和不對中比值有關,當不對中和不平衡的比值較大時,聯軸器不對中對轉子系統的影響明顯,當不平衡量和不對中量的比較大時,不平衡對轉子系統的影響明顯。

