超聲速單軌火箭橇動態載荷預示技術研究

楊 珍，范 坤，胡 兵，王一琰

(中國兵器工業試驗測試研究院， 陜西 華陰 714200)

火箭橇在火箭發動機推力作用下與滑軌通過滑靴配合連接，滑靴與軌道間存在間隙，火箭橇沿滑軌運動時，受到的軌道不平度、氣動載荷、火箭發動機振蕩燃燒以及地面效應作用而使得火箭橇動態載荷呈現出隨機性、沖擊性以及激勵力幅大且激勵頻帶寬等特點。單軌火箭橇試驗僅使用一條滑軌作為約束，具有試驗負載輕、氣動阻力小、動力需求低、可達到的速度和加速度高、試驗成本低等特點。單軌火箭橇試驗一般用于進行外形尺寸小、質量輕的戰斗部終點效應、導引頭拋罩、機載設備載荷沖擊等類型試驗，回收類試驗極少[1-3]。

火箭橇動態載荷最早由美國霍洛曼試驗基地提出，定義為火箭橇沿高精度滑軌運動所產生的結構振動載荷，通常指側向和豎向動態載荷，是結構設計人員進行橇體結構設計的一個重要依據，可為被試品提供力學環境依據、為結構設計和仿真分析提供載荷邊界條件，降低火結構設計參數冗余系數、提高火箭橇系統的推重比、錯頻提高運行的穩定性。隨著火箭橇速度提升至高超聲速，氣動效應、橇軌耦合作用的程度愈加嚴重，單軌橇作為高超聲速設計的首選橇型，能達到試驗所需更高的速度、加速度，但因僅使用單條滑軌進行約束，火箭橇運行過程中力學環境惡劣。在早期的火箭橇試驗中，由于缺乏相應的分析和試驗數據，火箭橇動態載荷設計主要依靠經驗公式計算或相似橇型比對結果進行結構設計，這使得火箭橇結構設計過于保守和被動，但設計人員從未停止過對火箭橇動態載荷的分析和試驗，一直在嘗試用不同的方法、從不同的角度對動態載荷進行預示，不斷提高火箭橇動力學分析能力，促進火箭橇試驗的高速化發展。

本文針對橇-軌耦合運動過程中橇體的振動特性問題，以2Ma超聲速單軌火箭橇為研究對象，采用有限元結構動力學仿真分析方法分析橇-軌耦合運動學和動力響應問題，對比分析理想平直軌和不平順軌兩種軌道模型工況條件下橇體測試點位的振動量，并搭載2Ma超聲速單軌火箭橇試驗進行驗證，試驗后對仿真數據和實測數據進行了對比分析。

1 火箭橇動態載荷預示方法研究現狀

火箭橇動態載荷的預測最早源于美國1961年出版的ISRACON手冊中提出的經驗系數(λ)法，用于解決軌道粗糙度對滑橇的作用，λ定義為速度的函數并作為慣性載荷施加于滑橇質心。Mixon和Krupovage分別于1971年和1985年首次給出了單軌和窄軌λ系數載荷[4]。由于火箭橇動態載荷數據的缺乏，Mixon提出了另外一種重要的動態載荷預測方法——沖擊參數(SIMP/SLEDYNEF)方法[5-6]，即采用瞬態有限元模態分析方法建立粗糙軌道的火箭橇柔性模型，滑橇與軌道界面剛度采用阻尼公式逼近。Greenbaum于1973年研制了SLEDYNEY軟件包，通過滑靴沖擊速度、火箭橇質量和豎向剛度得到SIMP系數和最大滑靴力。Hosser等于2000年提出了一種基于商業軟件包動態分析與設計系統的運動學方程數值積分方法[7]，即NIEOM法，這種方法對商業軟件DADS進行二次開發，根據實測數據定義了軌道豎向與橫向粗糙度，采用赫茲接觸理論、恢復系數或彈簧阻尼模擬滑靴沖擊，通過求解運動方程，得到橇體各離散質點的位移、速度、加速度、力和力矩等動力學參數。

國內僅對橇-軌耦合系統進行動力學建模和振動分析，沒有形成用于預示火箭橇動態載荷的方法。張雨詩等建立了火箭橇軌道系統的有限元模型并分析了其振動特性[8]，通過響應曲線、共振頻率及pinned-pinned振動頻率，得到了可能導致滑軌共振和pinned-pinned振動的火箭橇運行速度，并沒有對火箭橇的振動量值進行量化評估。王健自主開發RSTdyn軟件包，采用Newton-Euler法建立了橇-軌耦合系統動力學方程，對某單軌橇-軌系統進行了動力學響應計算及參數影響分析，得到了火箭橇、鋼軌及軌枕的加速度、速度、位移、接觸力等結構動態響應結果，表征了橇-軌系統相互作用的動力學特性[9]，但缺乏試驗驗證。

2 橇-軌耦合系統有限元建模及激勵源加載技術

2.1 橇-軌耦合系統模型

火箭橇和軌道耦合系統模型如圖1所示，包括火箭橇模型、滑軌模型、橇-軌耦合關系。以某超聲速單軌火箭橇試驗橇型為研究對象，最大運行速度700 m/s。火箭橇模型為一級推進結構，包括產品橇和一級橇模型，產品橇模型由被試品、橇體結構及其連接結構組成，一級橇模型由火箭發動機、橇體結構及其連接結構組成。滑軌系統由鋼軌、扣件、承軌梁等構成。橇-軌耦合關系指火箭橇通過滑靴包覆在工字型軌道上部，初始時刻滑靴上滑塊與軌道上表面接觸，滑靴側滑塊與軌頭左右側面、滑靴下滑塊與軌頭額面按結構設計值和磨損量預留一定間隙，火箭橇在發動機的推力作用下沿軌道航向運動，俯仰、偏航、側傾等運動被限制在很小的范圍內，滑靴與軌道之間存在接觸、碰撞、沖擊、摩擦、鑿削等耦合關系。

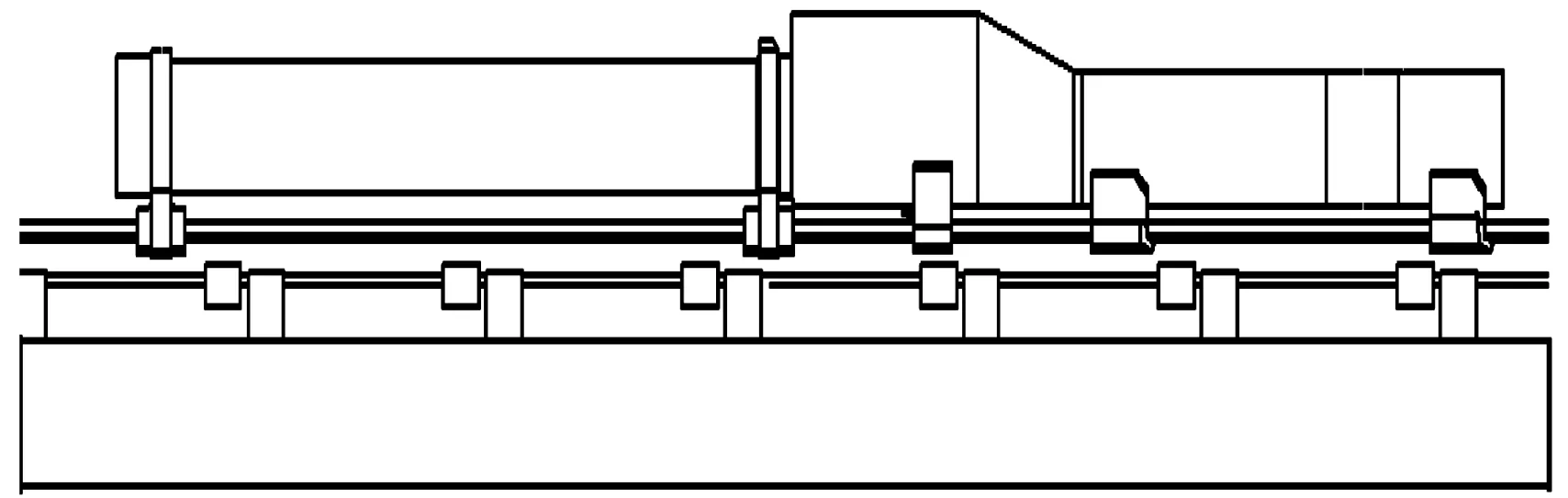
圖1 橇-軌耦合系統模型

火箭橇運行全程為9 km，全橇全系統直接建模非常復雜，必須對橇-軌耦合系統模型進行合理的工程簡化。包括以下幾個方面：

1) 火箭橇模型的簡化。主要包括連接部位的簡化、結構件直化和結構表面光滑處理。簡化的目的是為了便于進行網格離散。

2) 滑軌模型的簡化。由于軌道空間尺寸比火箭橇大很多，同時考慮到承軌梁由鋼筋混凝土構成，其重量非常大，因而在建立動力學模型時忽略掉承軌梁的振動，僅保留鋼軌模型；將扣點處U型板和壓板結構件的約束簡化為扣點與軌道接觸位置的面約束；最后，對于長程復雜性問題工程上一般采用分段計算，如高鐵機車軌道耦合動力學(分段長約30～50 m)，分段的長度與軌上運行車體的速度和動力學方程組的收斂性有關，本文采用200 m軌道模型進行計算。

3) 橇-軌耦合關系的簡化。建立火箭橇滑靴內腔與鋼軌五個面的配合關系，上滑塊與鋼軌上表面接觸、其余四個面與鋼軌按設計值或磨損量預留間隙，在動力學分析軟件中采用接觸表面靜動力摩擦的自動面面接觸碰撞類型表示火箭橇滑靴與鋼軌之間的接觸、碰撞、沖擊、摩擦等耦合關系。

2.2 橇-軌耦合系統激勵源加載技術

根據火箭橇與軌道實際結構與幾何尺寸，采用ANSYS軟件建立橇-軌耦合系統的有限元模型[10]，材料本構關系采用塑性材料模型，建立的有限元網格模型如圖2所示。

圖2 有限元網格模型

橇-軌耦合系統激勵源主要包括非定常氣動力、火箭發動機脈動推力以及軌道不平順。在火箭橇運行的全程中的某一典型速度點工況，假定系統的氣動力和發動機推力為定值。

1) 氣動力的加載。氣動力載荷包括氣動阻力和升力，這兩種力在火箭橇各部位值不同，將氣動力進行分區域加載。根據火箭橇氣動特性，將產品橇分為頭錐段、平直段、前滑靴和后滑靴4組部件，將推力橇分為推力傳遞裝置、阻力板、發動機3組部件，插值進行2Ma內橇體氣動仿真分析，提取以上部件在特定速度條件下的氣動阻力和氣動升力，在有限元軟件中通過節點力方式加載到橇體各部件表面節點上。火箭橇航向運行方向為航向正向，垂直軌道向上為豎向正向。最大速度工況各部件氣動阻力和升力如表1所示。

2) 發動機推力的加載。根據火箭橇質量、發動機推力、氣動阻力和摩擦力等邊界條件，計算火箭橇運行全程彈道曲線，提取最大速度時刻發動機推力。

3) 軌道不平順載荷的實現。采用徠卡激光跟蹤儀測量得到的軌道不平順實測數據建立空間3階多段樣條曲線，并根據軌道截面幾何參數建立特征面，由特征面和樣條曲線建立不平順軌道模型。

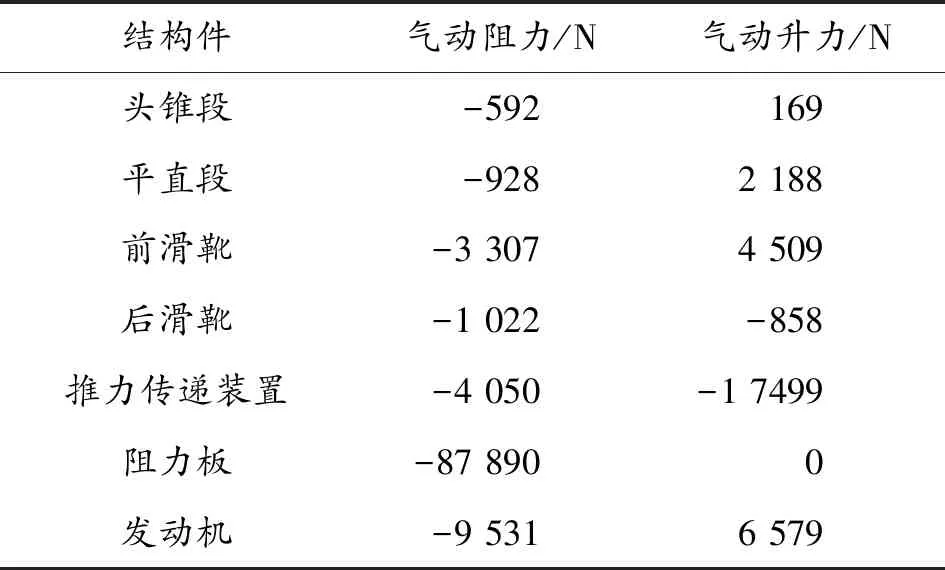
表1 最大速度工況各部件氣動阻力和升力

3 火箭橇動態載荷預示結果

根據火箭橇試驗振動傳感器布設位置及幾何尺寸，在計算模型中相應位置建立振動測量模擬測點。采用LS-DYNA動力學軟件對最大速度(700 m/s)條件下的理想平直軌和不平順軌兩種不同軌道工況下的有限元模型進行求解[11-12]，提取前滑靴和后滑靴振動模擬測量點位的航向、豎向和側向加速度-時間歷程曲線，分別如圖3和圖4所示。對理想平直軌和不平順軌工況下的振動曲線分別求400 Hz以內的均方根值(RMS)，如表2所示。

圖3 前滑靴三向振動曲線

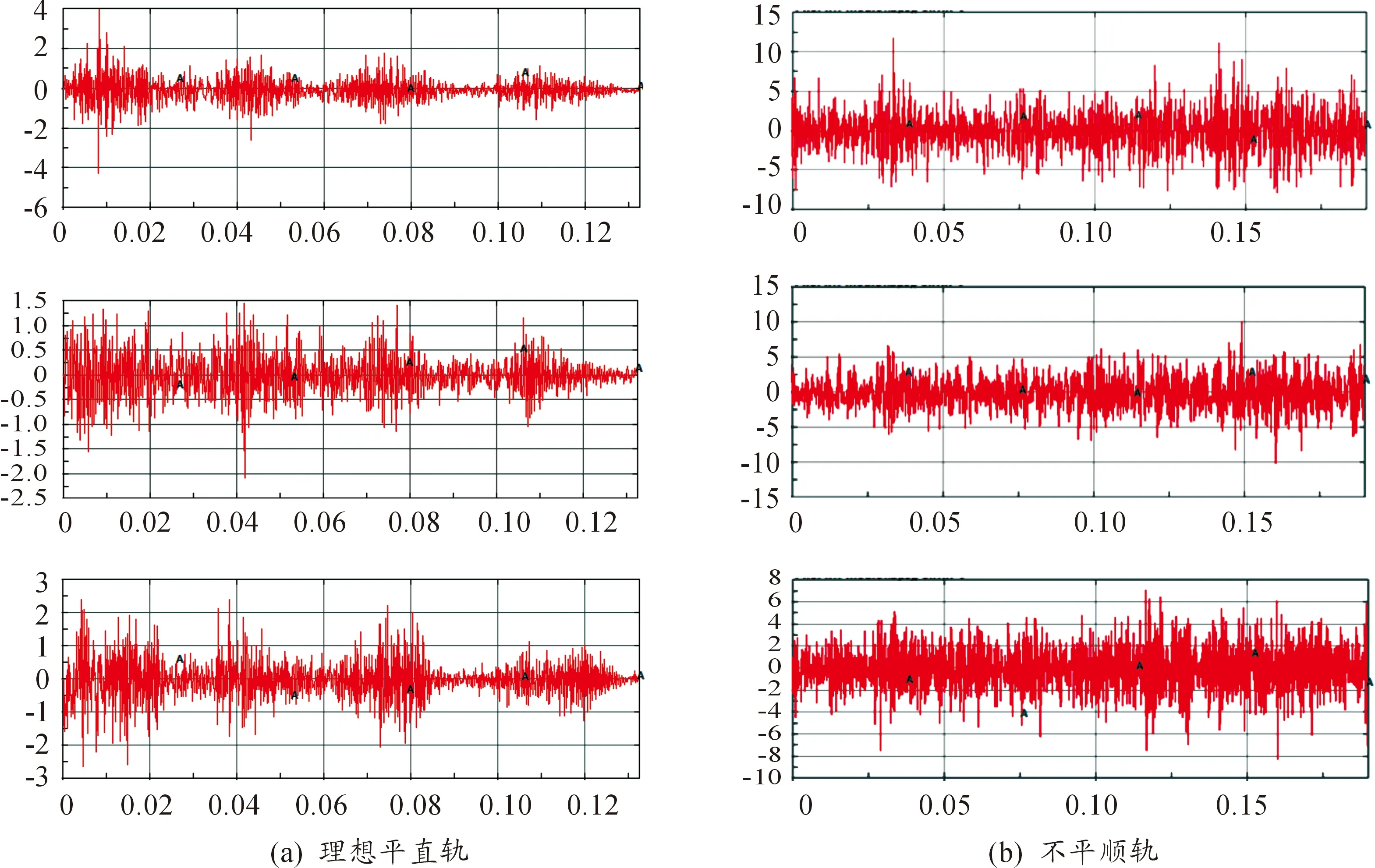
圖4 后滑靴三向振動曲線

由理想平直軌和不平順軌的加速度-時間歷程曲線可知：不平順軌的振動量明顯大于平直軌的振動量；平直軌的振動呈現明顯的周期特性且振動量值隨運行時間的增加而減小；不平順軌對火箭橇動態響應影響大，且隨機振動特性更為顯著，使用不平順軌模型更符合火箭橇在軌運行振動特性。

表2 振動RMS(g)值(400 Hz以下)

由兩種工況的振動RMS值可知：不平順軌的振動RMS值比理想平直軌各方向上的振動量值都大幾倍，且倍數關系不等；理想軌的前后滑靴振動RMS值相當，側豎向振動量相同；不平順軌的前滑靴振動RMS量比后滑靴大，豎向振動約為側向振動的0.5～0.6倍，這與文獻[4]中提到的側向載荷為豎向載荷的0.6倍相近。

4 驗證

在阿拉善9 km高精度滑軌上開展某超聲速單軌火箭橇試驗，在產品橇前滑靴和后滑靴上各安裝一枚振動傳感器，記錄與振動仿真預示相同位置處的振動環境。試驗后對產品橇前后滑靴振動傳感器的振動測試數據進行分析，三向振動曲線如圖5所示，圖中從上到下依次為航向、豎向和側向振動。

圖5 火箭橇試驗三向振動曲線

實測過載數據和理論彈道數據曲線如圖6所示，可知火箭橇運行2.8 s左右為最大速度時刻，由于過載實測數據和理論彈道數據存在誤差，因此從振動數據中分別提取2.6～2.8 s、2.8～3 s、3～3.2 s時間段的三向振動數據，進行400 Hz以下濾波得到三個時間段的振動RMS值如表3所示。

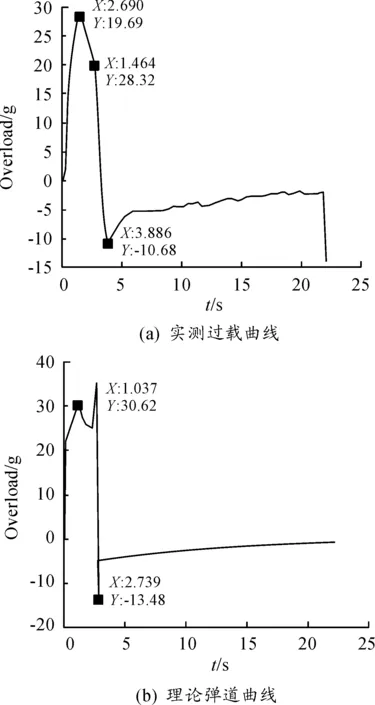
圖6 火箭橇試驗彈道曲線

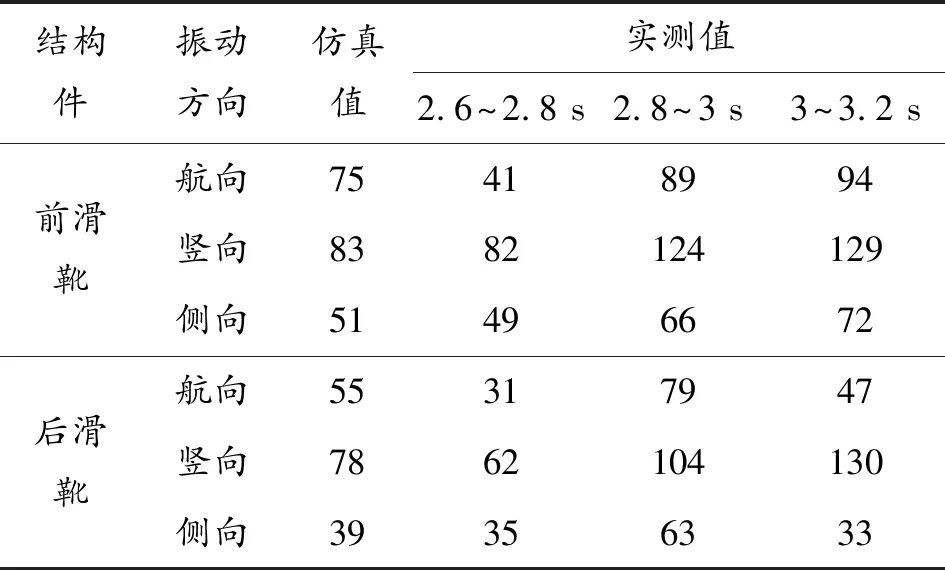
結構件振動方向仿真值實測值2.6～2.8 s2.8～3 s3～3.2 s前滑靴航向75418994豎向8382124129側向51496672后滑靴航向55317947豎向7862104130側向39356333

從最大速度時刻附近三組振動RMS值及其與仿真值看，前滑靴和后滑靴的豎向振動和側向振動與2.6～2.8 s時刻的振動RMS值呈現較好的一致性，平均誤差約10%左右；在而2.8～3 s、3～3.2 s這兩個時間段為產品橇和一級橇發生級間分離時間段，振動量較大，不具有可比性。航向振動量值尤其是頭部振動仿真與實測誤差較大，主要原因為仿真過程氣動力和發動機推力均為定值，未考慮試驗過程中的非定常氣動和發動機推力脈動，但工程實際中，動態載荷的預示通常為側、豎向振動量，而航向動態載荷一般以過載數據為準。

5 結論

1) 采用有限元結構動力學仿真分析方法計算得到的某一特定速度工況條件下的動態載荷預示結果與實測結果側、豎向振動量值具有很好的一致性；

2) 該方法可以為超聲速單軌火箭橇動態載荷優化設計及高馬赫數火箭橇動態載荷預示提供理論依據和數據支撐。