計及供電成本的小水電群經濟調度優化模型研究

夏 軍，葉 超，魏 潔，姜 鵬，董 軍，楊培文

(1.國網四川省電力公司雅安供電公司，四川 雅安 625000；2.北京中恒博瑞數字電力科技有限公司，北京 100085；3.能源市場研究所(華北電力大學)，北京 102206)

水資源作為一種可再生的清潔能源發電，相比火力發電以及核電等方式更加綠色環保。四川省是我國水資源貯藏大省，加上各小流域水電蘊藏量，蘊藏量可達1.64億千瓦左右，居全國第二位。雅安地處成都平原向青藏高原過渡地帶，相對高差較大，境內降水量充沛，2016年底雅安電網調度管理并網水電廠643座、發電機組1 315臺、水力發電總裝機185.117萬千瓦，裝機占比達99.92%。但雅安電網水電裝機占比較高，如何有效消納大規模水電己經成為雅安地方政府和電網公司亟待解決的問題。

由于江河來水周期性和季節性較強，水電調節性能總體較差，多年調節性能的水電站僅占21%，導致水電群出力在年內分布極不均勻，豐枯期出力懸殊，枯期平均出力僅為豐期平均出力的三分之一。除此之外，雅安當地并網的小水電站幾乎都是徑流式小水電，多在山區或離城市較遠的地區，具有規模小、設施老舊等特點，在現階段運行時，還存在兩個較為緊迫問題尚待解決，即過電壓安全問題和雅安地區電價倒掛現象。

為了提高雅安小水電本地就近消納，減少上網電量，合理規避價格倒掛等問題，將上述問題看作是小水電站群的經濟性優化調度問題。國內外學者提出了許多解決方法，如傳統規劃算法[1-2]和智能算法[3-4]兩大類。文獻[5]梯級小水電群中各水庫的發電引用流量作為決策變量，建立以發電量最大的梯級小水電群優化調度模型；文獻[6]考慮了機電和渦輪發電機的能量損失，將水電機組排程調度問題建模為一個非線性混合的0—1規劃問題，采用對偶分解的兩階段方法解決此問題；文獻[7]在保證大壩安全的前提下，以梯級電站在調度周期內發電量最大為目標，采用浮點數編碼的遺傳算法進行求解；文獻[8]考慮大小水電系統運行的經濟性和可靠性，考慮約束容忍度的改進粒子群優化算法求解協調調度優化模型；文獻[9-10]提出了大小水電可消納電量期望值最大短期協調優化調度模型，并應用啟發式搜索和關聯搜索方法進行求解。

綜上所述，本文以豐水期小水電富集的雅安地區為背景，針對雅安當地小水電站老舊設備的高故障率導致的高維修費和買賣電價格倒掛等問題，提出了小水電就地消納和提出了滿足當地負荷需求的建議。同時，考慮各個小水電站故障成本及折舊成本分攤，在滿足雅安地區負荷需求的基礎上，以地區供電總成本最小為目標，實現雅安當地小水電站的經濟調度。此外，本文選擇改進遺傳算法來解決上述優化調度問題。

1 基本原理

1.1 改進遺傳算法

遺傳算法(GA)是一種模擬達爾文自然選擇和遺傳機制。對于大規模小水電系統，由于電站數量多，在此問題中每個電站又分為24個時段。同時，每個時段每個電站又對應一個開停機的狀態變量，變量規模龐大，導致解空間隨變量的增加而急劇增長，求解時間大幅增加，計算效率難以滿足實際工程要求。因此，為了避免早熟，過早收斂導致產生局部最優解現象的發生，本文采用自適應模擬退火遺傳算法。

1.1.1自適應處理

首先算法具備較強的魯棒性和更高的計算效率，采用自適應函數來調整改良變異算子和交叉算子，即

(1)

(2)

式中，fm為要進行交叉處理的兩個個體中適應度較大值；favg為每代群體的平均適應度值；fmax為群體中最大的適應度值；f為要變異個體適應度值。其中pc1、pc2、pm1、pm2均為常數。

1.1.2模擬退火遺傳算法原理

該算法以增加種群多樣性為目的，在初始化狀態下種群足夠豐富和算法依舊保持種群多樣性特點，具體流程如圖1。

圖1 自適應模擬退火遺傳算法操作流程

具體步驟如下：

(1)初始化參數，參數包括種群規模M，進化代數G，交叉概率Pc，變異概率Pm。

(2)初始化種群1，2，3，計算種群中各個個體的適應度值f。

(3)進行選擇、交叉、變異操作，生成子代個體，計算子代個體的適應度f。

(4)判斷是否滿足接受函數，若是，接受新個體，否則以一定概率接受新個體。

(5)對新個體進行降溫操作。

(6)判斷值是否滿足預期函數值，若是，輸出最優解，否則轉到第3步。

在算法運行過程中，初始參數選擇尤為重要，其中Pc和Pm通過自適應函數求解。本文采用的算法包含外循環和內循環兩種模式，即外循環為遺傳算法，控制著最優解的決定權；內循環為模擬退火算法，主要控制降溫操作，以跳出局部最優解，從而具有更大可能性去獲取全局最優解。

1.2 成本分攤計量

由于某些小水電站的設備老化嚴重，故障率較高，因此針對該類小水電站的折舊成本及維修成本按其發電量分攤計量，來判定該類水電站發電的經濟性。

1.2.1折舊成本分攤計量

水電機組n的單位電量折舊費用為Cdn，水電機組n總投資為In，使用壽命周期為Y，機組n殘值為In′，水電機組n的年均發電量為Qn，則其按電量分攤的折舊成本為

(3)

1.2.2故障維修成本分攤計量

水電機組n的單位電量故障維修成本分攤為Cmn，則其計算表達式為

(4)

式中，C0為單次工人維修費用；PnλToff為機組n因維修停止發電運作而損失的利益；其中Pn為機組n的裝機容量；λ為銷售電價；Toff為機組停止運作的時間；a為機組n年故障維修次數。

2 小水電站經濟調度優化模型

由于雅安當地發電電源幾乎全部為小水電站，呈混聯分布，且有部分水電站之間也存在上下游水量聯系，因此模型的搭建需考慮上游電站水量對下游電站的影響，在建立水量平衡關系式時，需根據有無調節能力將小水電站分為兩類。最后以雅安地區系統供電成本最小為目標搭建經濟調度優化模型，即

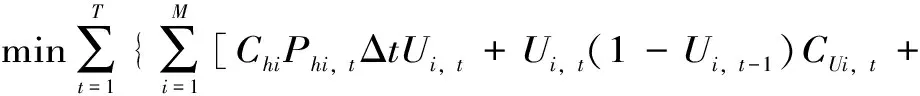
Ui，t-1(1-Ui，t)CDi，t]+ptΔPt}

(5)

Chi=Cdi+Cmi

(6)

Phi，t=Ai×qi，t×hi，t

(7)

(8)

式中，Chi表示第i個水電站的單位發電量固定成本分攤；Cdi表示第i個水電站的單位發電量折舊分攤；Cmi表示第i個水電站的單位發電量故障維修成本分攤；Phi，t表示第i個水電站t時段的出力；Ai表示第i個水電站的出力轉換系數；qi，t表示第i個水電站t時段的發電引用流量；hi，t表示第i個水電站t時段的平均水頭；Ui，t表示第i個水電站t時段的開停機狀態，0表示開機，1表示停機；CUi，t和CDi，t分別為啟停機成本；pt為t時段電價，Pt為t時段需求側負荷功率；M為水電站的總數量。

約束條件具體如下：

(1)庫容約束

vi，min≤vi，t≤vi，max0

(9)

(2)發電引用流量約束

qi，min≤qi，t≤qi，max

(10)

(3)水量平衡約束。針對水量平衡約束，分為有水庫有調節能力的水電站水量平衡公式

vi+1，t+1=vi+1，t+(ni+1，t-Qi+1，t+Qi，t)Δt

(11)

無水庫徑流式小水電站水量平衡公式

ni+1，t+Qi，t=Qi+1，t

(12)

(4)功率平衡約束

(13)

(5)下泄流量約束

Qi，min≤Qi，t≤Qi，max

(14)

(6)水電站出力約束

Phi，min≤Phi，t≤Phi，max

(15)

(7)機組最小運行時間約束

(Ui，t-Ui，t-1)+(Ui，t+v-1-Ui，t+v)≤1，
t∈1，2，…，(T-v);v∈1，2，…，(Ton-1)

(16)

(8)機組最小關停時間約束

(Ui，t-1-Ui，t)+(Ui，t+v-Ui，t+v-1)≤1，
t∈1，2，…，(T-v);v∈1，2，…，(Toff-1)

(17)

(9)末水位控制約束

(18)

3 算例

3.1 情景設置

雅安某區域小系統豐水期日前經濟調度，發電機組全為水電機組，共計5個水電站，即H1、H2、H3、H4、H5，系統內部全天供電量大于系統用電需求量。其中，水電站H1、H2是擁有水庫有日調節能力的兩座可調節小水電站，其余水電站都為不可調節的徑流式水電站，各水電站特征基礎數據見表1。

此外，水電站H1和H2最小庫容(死庫容)分別為133.4萬m3和383萬m3，最大庫容分別為1 575.1萬m3和1 492萬m3，水庫正常水位分別為792 m和327 m，死水位分別為758 m和302 m。同時，水電站H3、H4和H5均是無水庫。

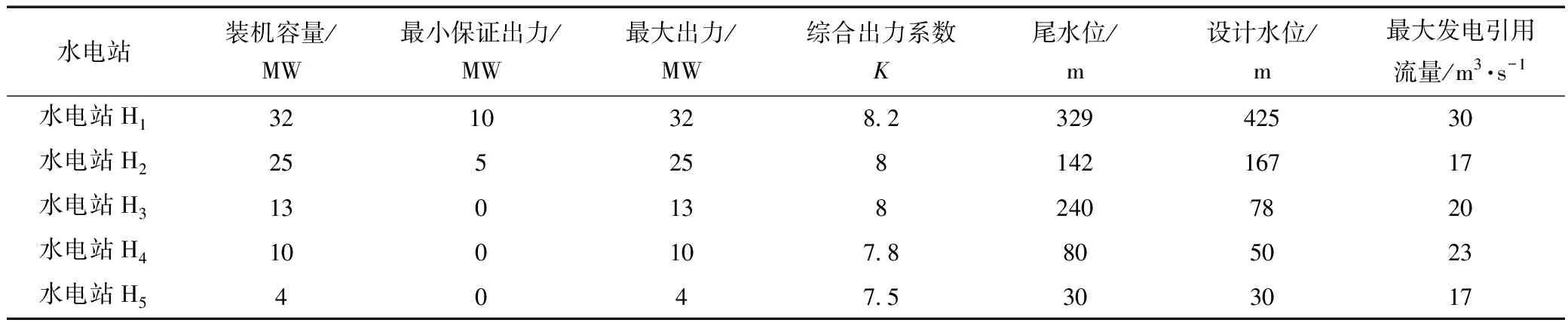
表1 基礎數據

在上述大背景下，本文設置兩個情景：

(1)所有水電站滿發，富余電量統一上網。由于處于豐水期，該區域所有水電站發電的供電量大于當地的負荷需求量，存在部分富余電量，該場景在滿足當地負荷需求后，其余全部富余電量按照當地上網電價默認全部賣給四川省主網。

(2)水電站根據成本排序，以經濟性為目標，在不同時刻以成本最低為原則，在滿足總需求的基礎上，同時與省主網有電量交互。當水電站的發電成本高于省主網購電價格時，該水電站會停止發電；若低于省主網購電價格，保持開機發電狀態。

3.2 模擬仿真

該模擬仿真的計算條件如下所示：

(1)假設水電站的自然來水量均為確定的。

(2)設定為24時段日前調度，針對不同時段設置豐水期電價和峰谷平電價，其中高峰時段為7∶00～11∶00，19∶00～23∶00，低谷時段為23∶00到次日7∶00，平段為11∶00～19∶00。

(3)設定電價變動，銷售側豐枯電價具體變動為：在平水期豐水期電價下浮5%。峰谷分時浮動電價按高峰時段在豐枯浮動基礎上上浮50%，低谷時段在豐枯浮動基礎上下浮50%；上網側取消峰谷電價，僅設置豐水期電價在平水期價格基礎上下浮24%。按照此規則變動后的豐水期下網峰谷平電價分別為：0.567 15元/(kW·h)，0.378 1元/(kW·h)，0.189 05元/(kW·h)；豐水期上網電價為0.08元/(kW·h)。

(4)雅安某區域小系統的第二天需求側預測日負荷曲線如圖2，看出存在3個尖峰，分別為早上6∶00～8∶00，中午11∶00～13∶00及晚上18∶00～20∶00 3個時段。

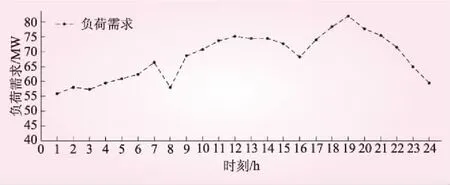
圖2 雅安某區域日負荷曲線

(5)各水電站發電引用流量下限為0，上限為最大發電引用流量。

(6)改進遺傳算法參數設置如下，種群數量n=50，最大進化迭代次數為g=100，pc1=0.8，pc2=0.5，pm1=0.1，pm2=0.01，初始溫度T0=100，依照章節1.2中給出的算法步驟逐步降溫到終止溫度。

本模擬仿真運用Matlab軟件實現，將設定好的參數代入所建模型的目標函數和約束條件中，再代入編寫的程序算法中進行計算。考慮到遺傳算法結果的不確定性，每次的運算結果都會有差異，本文對該模型進行10次模擬仿真，最終結果最終取10次仿真結果的平均值。各小水電站的出力情況如表2。如上圖表，總結水電站優化調度結果，從開停機狀態及出力情況展開分析。首先從機組開停機狀態分析，水電站H1、H2、H324 h內都處于開機狀態；水電站H4在9∶00～22∶00處于開機狀態，其余時間段處于關機狀態；水電站H5只在11∶00～13∶00和18∶00～20∶00兩個時段開機，其余時段關機。再從出力水平分析，水電站H1、H2、H4開機時段內幾乎都處于滿發狀態；水電站H3除0∶00～4∶00處于未滿發狀態，其余時段均處于滿發狀態；水電站H5開機時段都處于未滿發狀態。

出現上述調度優化結果，原因為各水電站單位電量的固定成本分攤不同。下表3為各水電站投資成本和運營成本的相關基礎數據，根據1.2所述的成本分攤計量方法求得各小水電站單位電量固定成本分攤。

表1中，可看出各水電站單位電量的固定成本分攤H5>H4>H3>H2>H1，上述結果是由于各水電站設備老舊化程度不同造成的，水電站H3、H4、H5設備老舊化較為嚴重，在日常運行中，故障率較高，維修費用較高，導致單位發電量的折舊成本和故障維修成本分攤較高，其中水電站H5設備老舊化最為嚴重，其固定成本分攤最高。

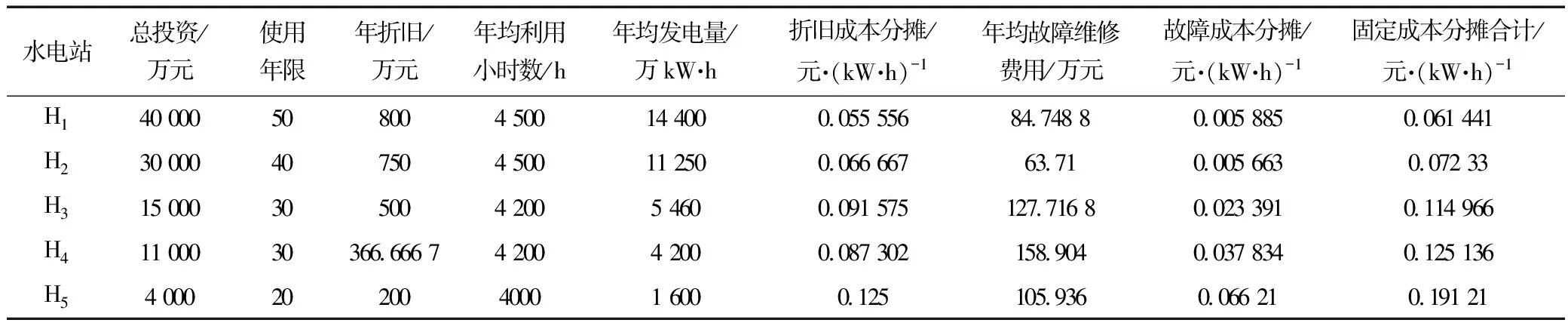
表3 各水電站固定成本分攤

表4 情景總成本對比分析 元

為追求系統總成本最小，因電站H5單位電量的固定成本分攤在5個水電站中最高，該電站在谷時段和平時段發電成本高于上網電價，在電量富余的狀態下，該電站的發電不經濟，因此該電站只在兩個峰時段發電，起到調峰作用，其余時段選擇不發電；水電站H1、H2固定成本分攤最低，低于上網電價，作為基負荷24時段滿發；水電站H3、H4相比H1、H2固定成本分攤較高，雖高于上網電價，但低于從省主網購電價格，因此可用來填補谷時段和平時段的負荷差，根據負荷需求安排機組出力，擬合負荷曲線。最后，針對系統運行總成本對比分析，其中場景2分別采用一般遺傳算法和改進遺傳算法求解，結果如表4。

可以看出豐水期調度優化前系統調度總成本(情景1)遠高出考慮設備老舊化程度及其固定成本分攤等因素的優化調度總成本(情景2)，在于不考慮設備老舊化程度及其固定成本分攤等因素，全時段滿發，富余電量上網賣出這種調度決策行為不夠經濟，因其發電運行成本已高出上網電價，這部分富余電量只會造成額外成本。相比之下，情景2以水電站機組的固定成本分攤為根據，將各小水電站發電進行排序，成本低者先發電，成本較高者用來調峰或者不發電，該優化調度從系統供電成本最低出發，考慮機組發電的經濟性問題，調度安排更為合理，系統供電總成本最小。

其次，改進遺傳算法求得的最終供電總成本要低于傳統遺傳算法，在于傳統遺傳算法由于易過早收斂，導致早熟，最終求得的最優解僅為局部最優，并非全局最優，使出力總曲線與負荷需求曲線擬合程度較差，殘余偏差負荷較大，如下圖3a所示，導致最終電網電量的交互成本大幅升高。相較之下，由于改進遺傳算法全局搜索能力強，在求解運行過程中，可接受當前不是最優解的概率存在，因而可跳出局部最優情況，達到尋求全局最優解的目標，如圖3b所示，水電站總出力與日負荷曲線偏差較小，電力交互成本大大較低，進而降低了總成本，優化效果更明顯。

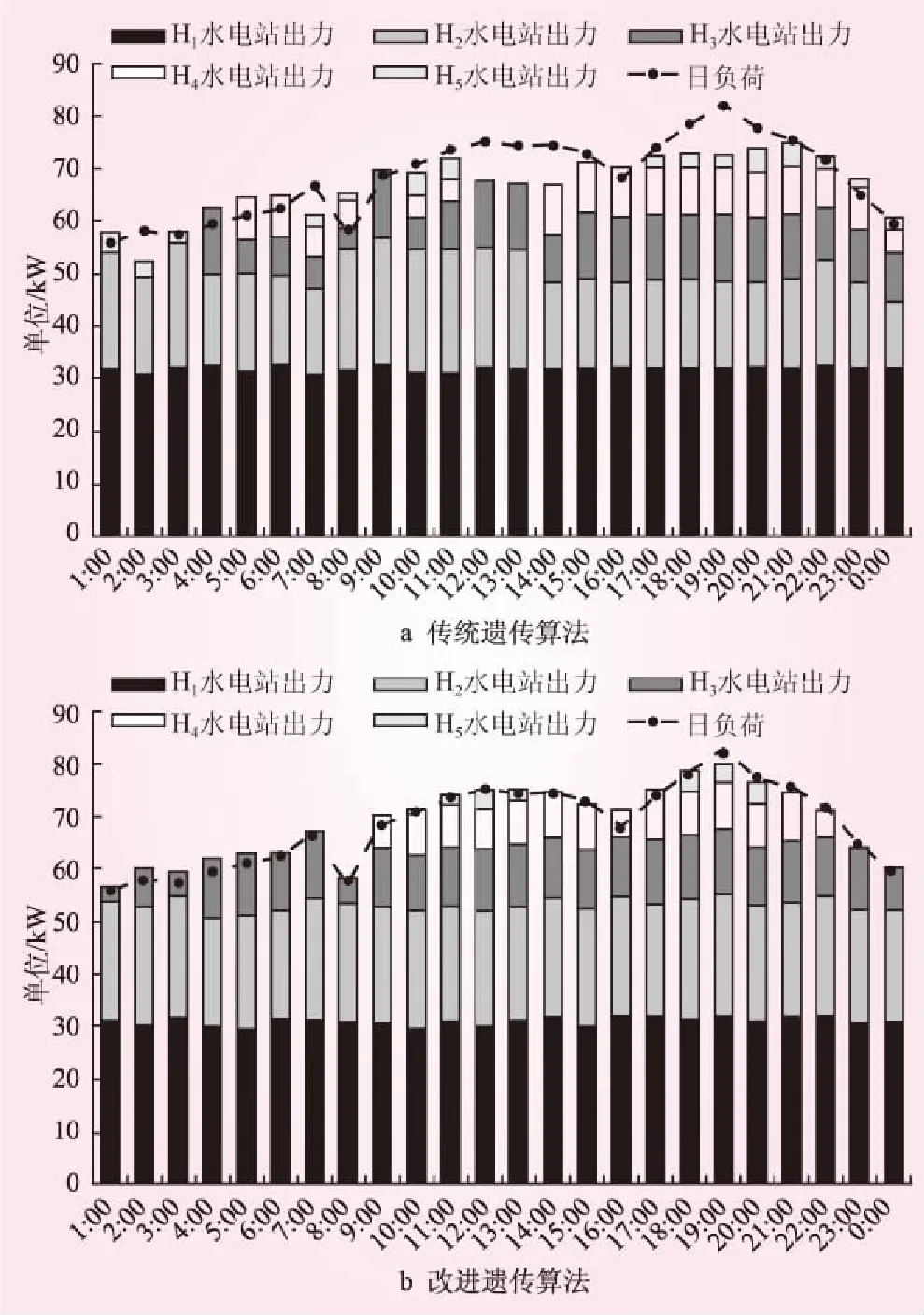
圖3 傳統遺傳算法與改進遺傳算法優化結果對比

4 結 論

(1)相比傳統遺傳算法，利用改進遺傳算法求解多變量和多約束條件的非線性整數規劃問題，全局搜索能力更強，避免了早熟現象的發生，使得計算結果更接近于全局最優解，優化效果更佳。

(2)同時從系統優化的整體性出發，考慮水電設備新舊程度，將年折舊成本和故障維修成本分攤到單位發電量中，再衡量判斷水電站發電的經濟性，最終指導雅安當地小水電群調度安排，將單位電量成本分攤較高水電站頂峰發電或者停機不發電。

(3)在一定程度上能夠合理減少雅安當地小水電設備因老化嚴重，頻繁發生過電壓安全事故而帶來高額的故障維修成本，同時規避了售電電價的價格倒掛等經濟性問題，對降低雅安當地電力系統的供電成本，推動當地小水電產業的發展具有重要研究價值和意義。