基于ABAQUS的Lamb波橢圓法探傷的仿真分析
王高平,魏 鳴,石 政,徐 博
(武漢工程大學 機電工程學院,湖北 武漢 430205)
0 引言
隨著我國工業化進程的高速發展,工業化產品及其設備已普遍應用于社會的各行各業,而這些產品的結構離不開板狀結構。板狀結構在加工成型的過程中會產生缺陷,為避免發生設備故障和安全事故,及時發現板件缺陷和分析缺陷很重要[1]。
蘭姆(Lamb)波在檢測薄板結構時不會出現擴散衰減,與金屬薄板的中性面相比,Lamb波傳播時會出現頻散現象而形成多種模態,其速度依賴于頻率和厚度之積(頻厚積)[2]。隨著波的頻率和板件厚度的改變,其模態也隨之改變,所以,在研究Lamb波的傳播特性時,Lamb波的頻散曲線很重要。利用MATLAB編程求解Lamb波波動方程,得到其頻散曲線,來確定頻厚積與模態間的關系,為仿真奠定基礎[3]。
本文基于橢圓定位法則[4],運用ABAQUS軟件對Lamb波在鋁板中的傳播過程進行仿真。分別建立健康、缺陷鋁板模型并進行網格劃分,計算時間步長和增量步長,加載中心頻率為250 kHz的漢寧窗調制波,分別得到健康、缺陷鋁板的x-y圖和差信號圖,并進行分析和計算,從而確定損傷的具體位置[5]。
1 Lamb波的頻散特性
Lamb波被廣泛應用于結構健康監測中,它是一種在厚度與激勵聲波波長為相同數量的聲波導中、由縱波和橫波相互耦合而成的一種彈性波,在薄板中有對稱和反對稱兩種傳播形式。頻散特性是主動Lamb波在薄板中傳播的主要特性之一,它主要描述了頻厚積改變時Lamb波的相速度(群速度)的變化趨勢。在自由邊界條件下,各向同性材料薄板的Lamb波表面波的頻散方程[6]為
(1)
(2)
(3)
cp=ω/k
(4)
(5)
d=h/2
(6)
式中:k=ω/cp為Lamb波波數,ω=2πf為Lamb波的角頻率,f為Lamb波的頻率;h為薄板厚度;cT,cL分別為Lamb波橫波和縱波波速;cp,cg分別為Lamb波的相速度和群速度[7]。
根據式(1)~(6)求出鋁板中cT=3 090 m/s、縱波波速cL=6 390 m/s[8]。式(1)中,冪次取+1與-1,分別表示Lamb波對稱和反對稱模態方程,利用圖解法和二分法,用cL、cT、cp將整個區間分為4個,分別對對稱和反對稱模態方程進行求解,借助MATLAB的編程和繪圖功能求解方程,且繪制出群速度和相速度的頻散曲線,如圖1、2所示。
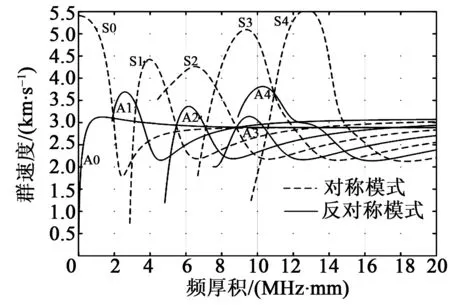
圖1 Lamb波群速度頻散曲線圖
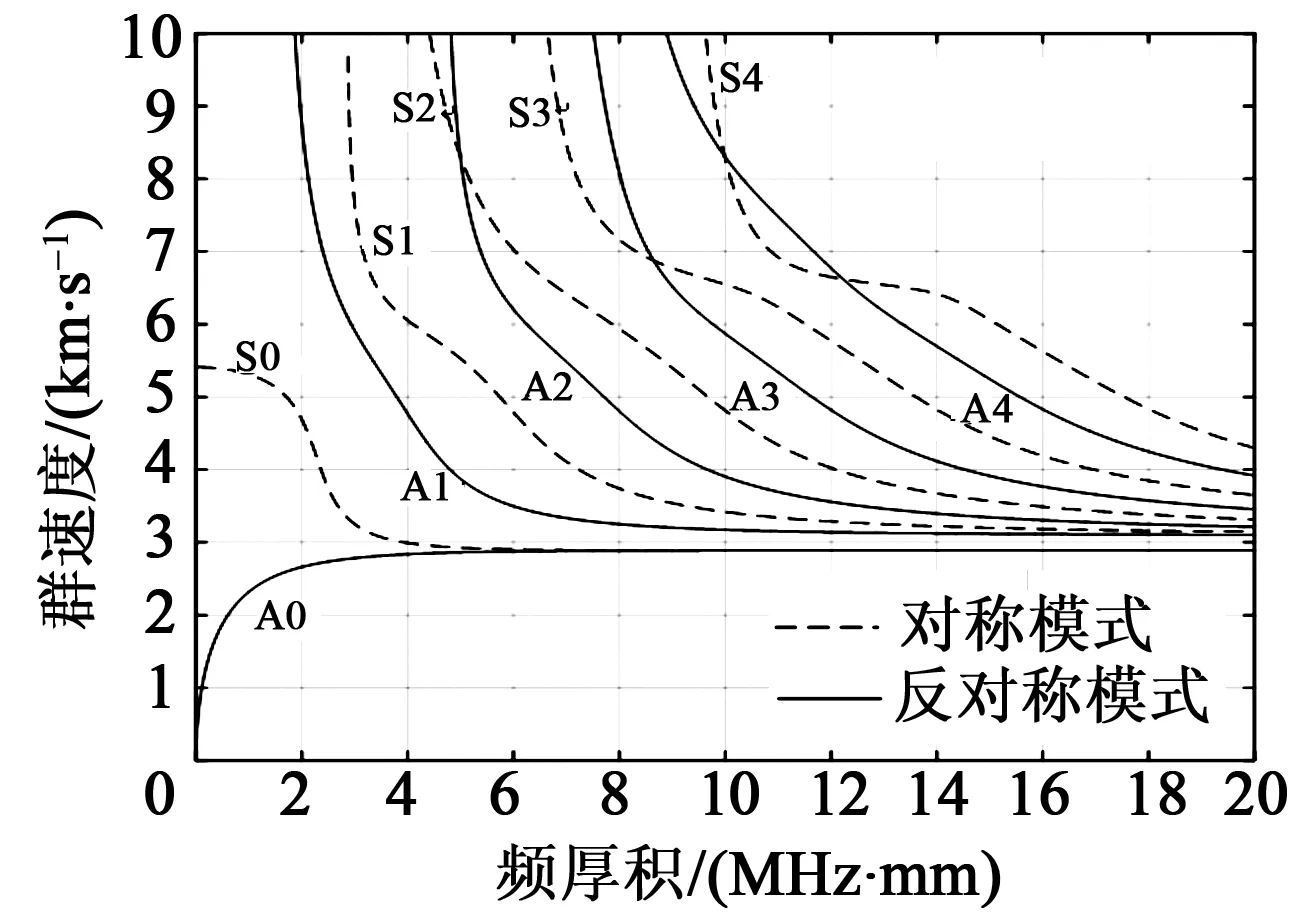
圖2 Lamb波相速度頻散曲線圖
由圖1、2可看出,任意一個頻厚積至少對應2種或以上的模態,隨著頻厚積的增加,模態的形式越復雜,這也是Lamb波在薄板中的頻散現象,由于多模態對后期數據處理制造很大的障礙,為了便于分析,盡量只激發單模態下的Lamb波,即頻厚積選擇1 MHz·mm。
2 Lamb波激勵信號的參數選擇與加載方式
本次研究采用窄帶激勵的方式產生Lamb波激勵信號。通常采用加窗函數對正弦信號進行截取的方式來獲取Lamb波的窄帶信號,這里選取加載漢寧窗進行激勵,Lamb波激勵信號[9]為
(7)
式中:fc為激勵波形的中心頻率;t為激勵波形傳播時間;n為正弦波周期數目。
由圖1可知,隨著頻厚積的逐漸增大,Lamb波發生頻散現象,且每個模態的速度都不同,這樣會使后期的信號處理復雜化。在Lamb信號處理的應用中,通常只激發Lamb波的S0和A0模態來進行分析,即頻厚積選擇1 MHz·mm來激發單一模態的Lamb波。綜上所述,選擇中心頻率250 kHz、周期數目5、幅值10 V的Lamb波作為激勵信號。將式(7)展開可得
(8)
由式(8)可看出,Lamb波是由3個正弦函數疊加而成,在設置載荷時需加載3個正弦周期函數。圖3為激勵信號時域圖。
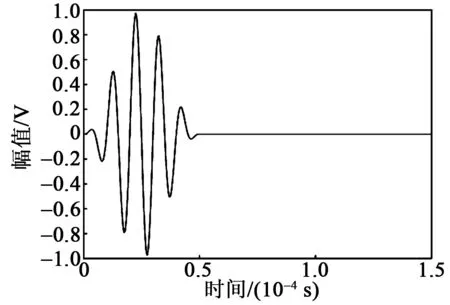
圖3 Lamb波激勵信號時域圖
3 橢圓法定位薄板損傷的仿真分析
本次研究以橢圓法定位為基礎實現損傷識別[10]。對損傷的板件進行檢測時,如果損傷位置不在檢測路徑上,那么觀測點B會收到兩部分信號,一部分是從激勵點A直接傳入,另一部分是經損傷信號反射而傳入,如圖4所示。因此,在處理數據時,將同一觀測點處的損傷鋁板信號與健康鋁板信號相減,即可只攜帶損傷信息的信號。
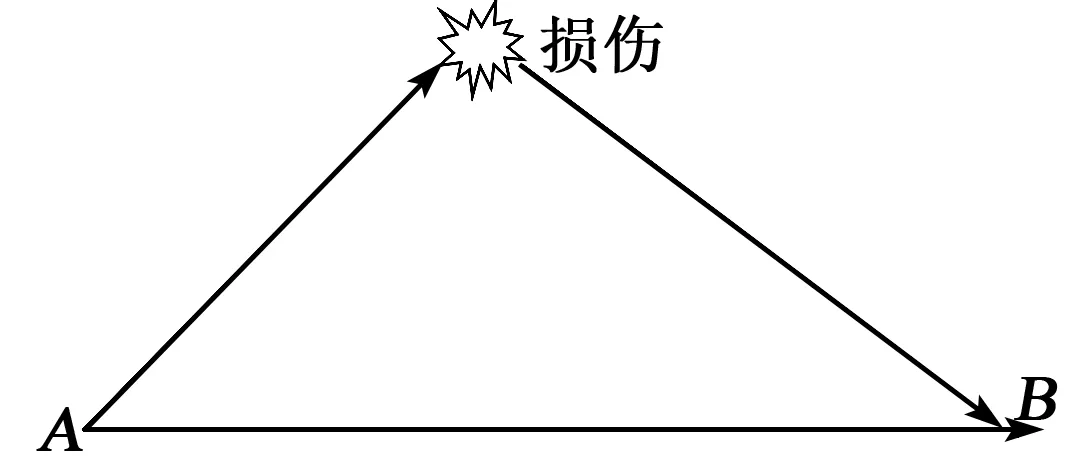
圖4 Lamb波在損傷鋁板中的傳播示意圖
3.1 Lamb在健康鋁板中傳播的有限元分析
本次仿真對象為鋁板,其長為400 mm,寬為400 mm,厚為4 mm,密度ρ=2 700 kg/m3,彈性模量E=70 GPa,泊松比υ=0.33。激勵信號選擇中心頻率為250 kHz、周期為5的漢寧窗調制信號。
激勵信號的激勵點A設置在模型的左端,入射角為45°,觀測點B、C分別設置在右上角和左下角,缺陷位置位于板中心,長為12 mm,寬為8 mm。建立的模型如圖5所示。
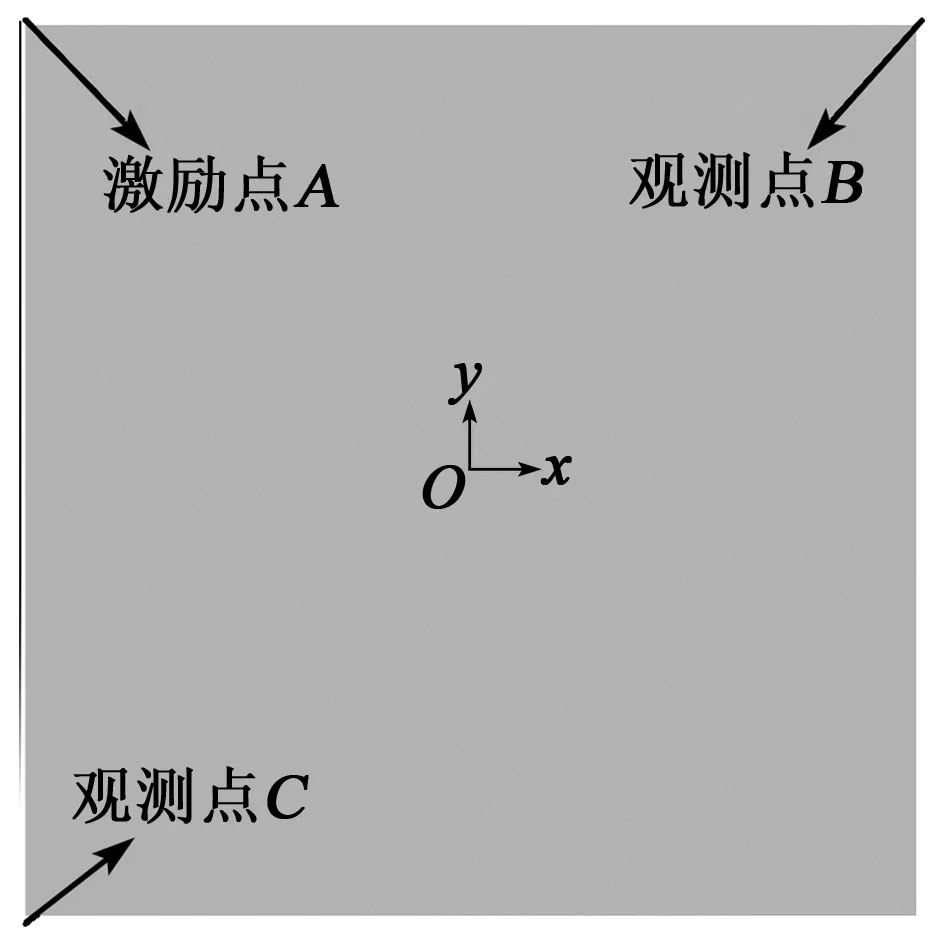
圖5 健康鋁板的模型圖
為了保證結果的穩定性采用顯性動力分析,積分單位選取典型代表性的8節點線性減縮單元(C3D8R)。網格劃分遵循一個Lamb波波長至少橫跨10個網格單元,以達到精度要求[11]。時間步長需滿足Lamb波在鋁板中傳播所花費的時間,根據時間增量準則,激勵信號的最大頻率對應的最小周期時間必須大于20個時間增量步長[12]。綜上所述,最小網格單元長度設置為1 mm,時間步長為3 ms,時間增量步長為40 ns。對設置好的健康鋁板模型加載激勵信號,并進行數值模擬仿真,計算后分別得到觀測點B、C的x-y圖,如圖6、7所示。
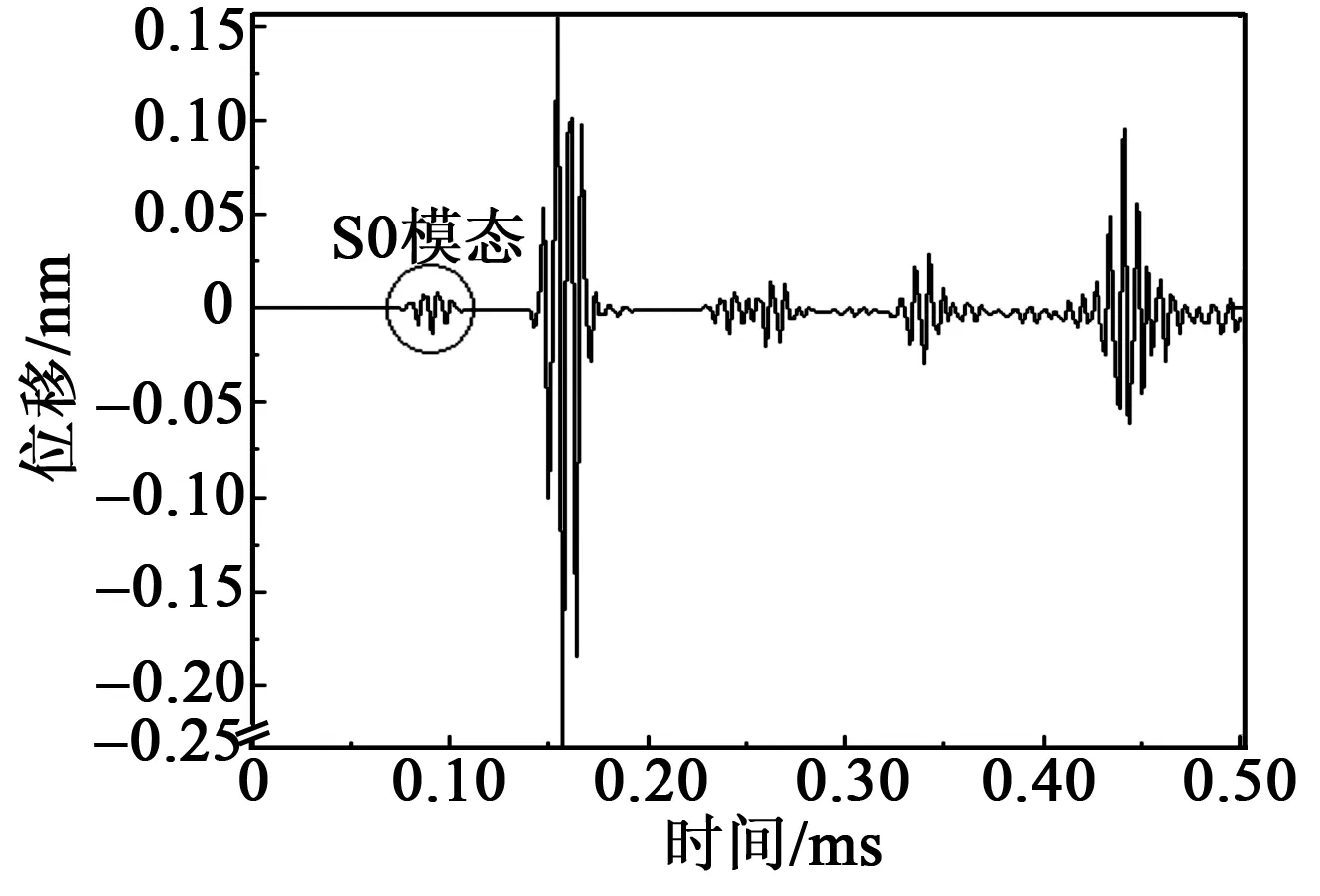
圖6 觀測點B處健康鋁板的Lamb波傳播圖

圖7 觀測點C處健康鋁板的Lamb波傳播圖
3.2 Lamb波在損傷鋁板中的有限元分析
鋁板的參數不變,損傷的位置設置在鋁板中心,長12 mm,寬4 mm,激勵點與觀測點位置不變,建立的模型如圖8所示。
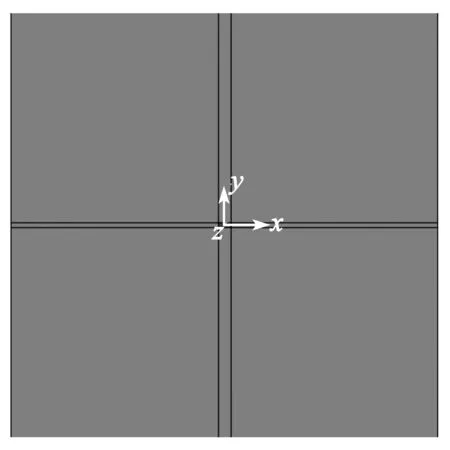
圖8 損傷鋁板的模型圖
對設置好的健康鋁板模型加載激勵信號,并進行數值模擬仿真,計算后分別得到觀測點B、C的x-y圖如圖9、10所示。
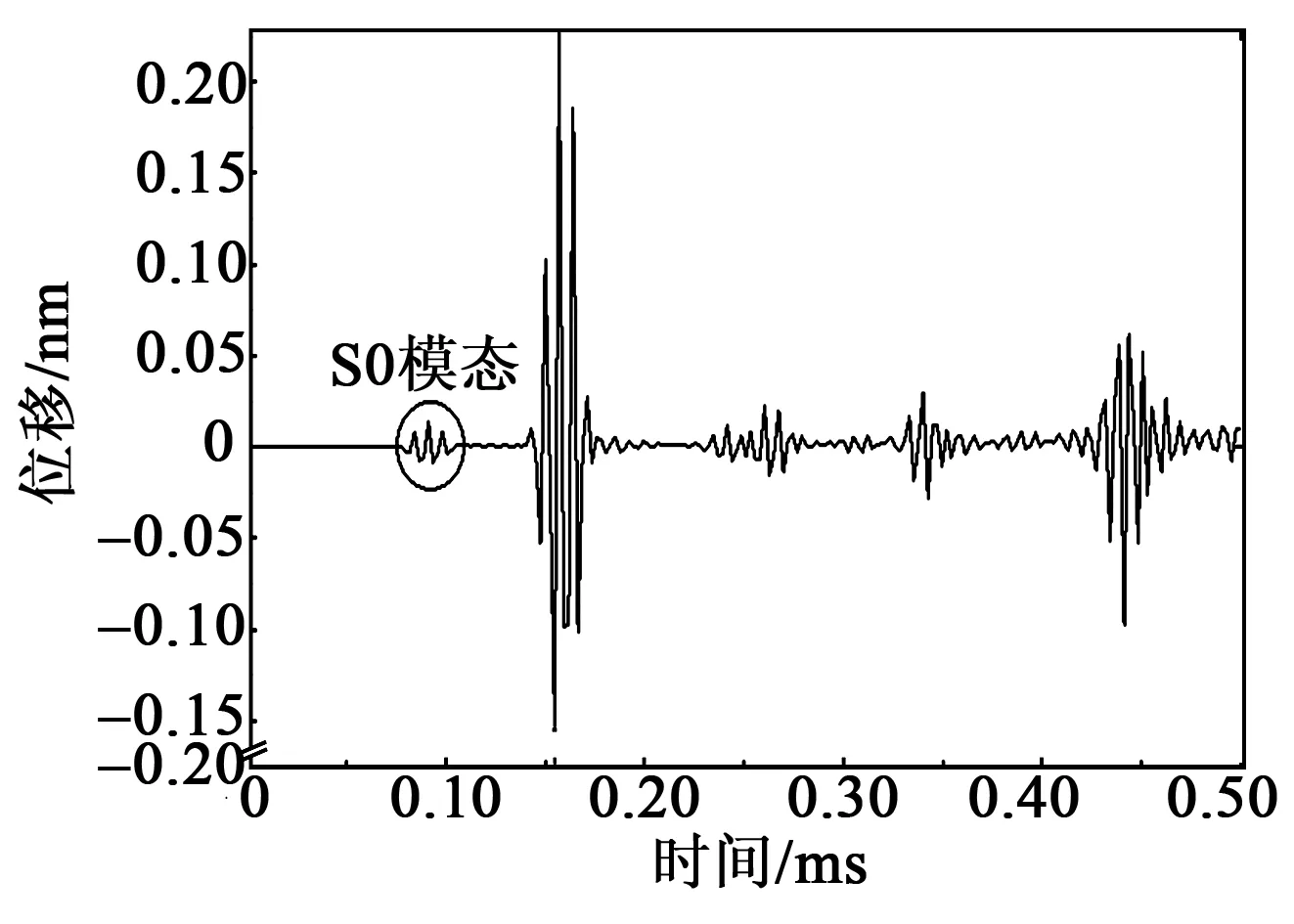
圖9 觀測點B處損傷鋁板的Lamb波傳播圖
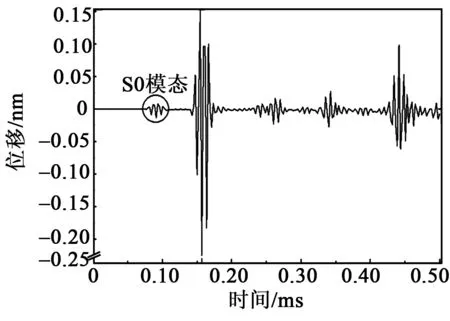
圖10 觀測點C處損傷鋁板的Lamb波傳播圖
為得到只攜帶損傷信號的x-y圖,分別將B、C點的損傷鋁板信號與健康鋁板信號相減,得到B、C兩點的差信號,如圖11、12所示。
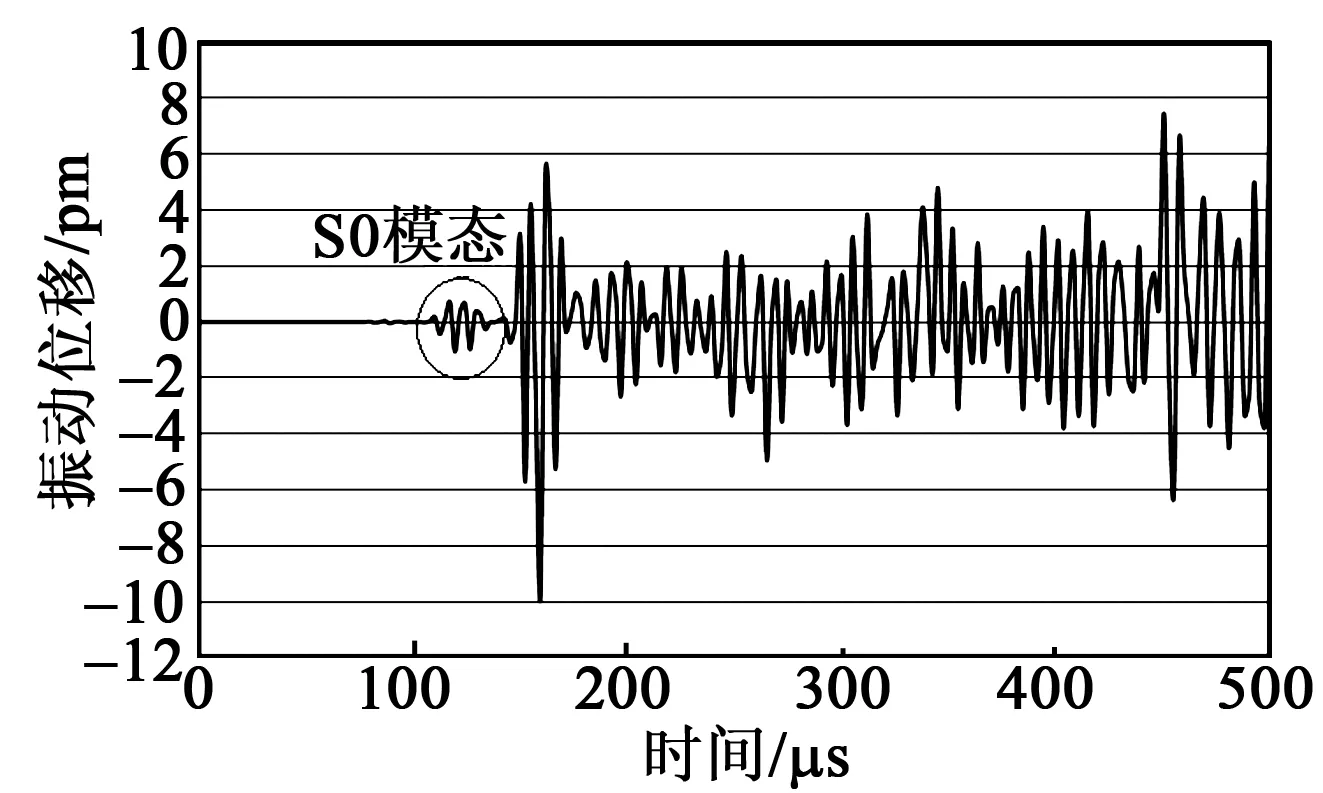
圖11 觀測點B處差信號的Lamb波傳播圖
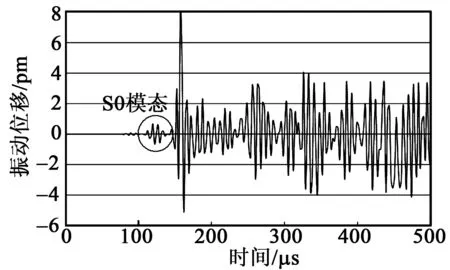
圖12 觀測點C處差信號的Lamb波傳播圖
由圖11、12可看出,Lamb波在傳播過程中發生多次反射形成疊加,這里使用S0模態的Lamb波信號來進行損傷定位(見圖6、7、9~12)。由圖1可看出,S0模態下的波速大于A0模態下的波速,即出現的第一個模態為S0模態,將模態的波峰值處的時間作為波在板中的傳播時間,通過ABAQUS的x-y圖查找功能分別查找各信號的S0模態傳播時間和幅值大小,其中差信號表現出僅由損傷引起的傳播信號,得到最終數據如表1所示。損傷定位圖如圖13所示。

表1 ABAQUS仿真數據
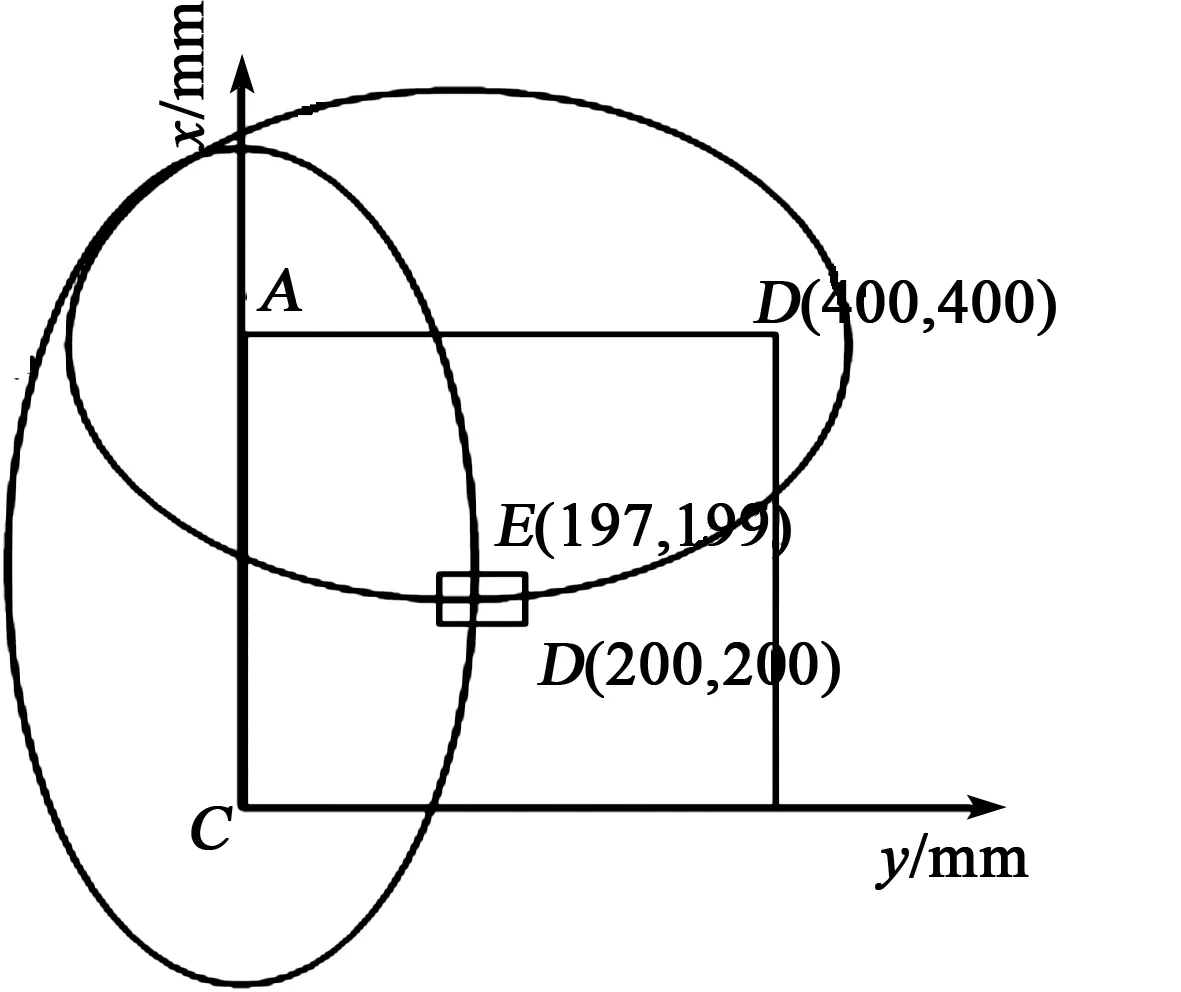
圖13 損傷定位圖
由圖1、2可知,在頻厚積為1 MHz·mm處的群速度為5 311 m/s,由S=v·t(其中S為Lamb波的傳播距離,v為Lamb波的群速度,t為傳播時間)可求出AE+EB=560.3mm,AE+EC=565.8 mm,而所建立的模型中AE+EC=AE+EC=565.7 mm,由此可確定損傷的位置(見圖13)。
理論損傷位置E與實際損傷位置D橫坐標相距3 mm,縱坐標相距1 mm,誤差極小。由圖13可知,該模型的檢測范圍是以A為原點,AC、AB為邊界的區域,當損傷位置處于AB或AC線路時,即激勵點、損傷點和觀測點處于同一直線上,可將模型簡化成監測路徑上的Lamb波檢測。將損傷位置E點至于B點,則監測路徑上的損傷定位圖如圖14所示。提取A點處的x-y圖如圖15所示。
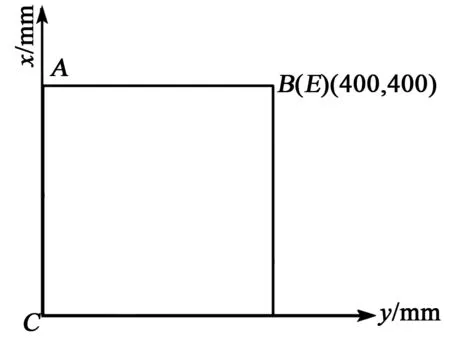
圖14 監測路徑上的損傷定位圖
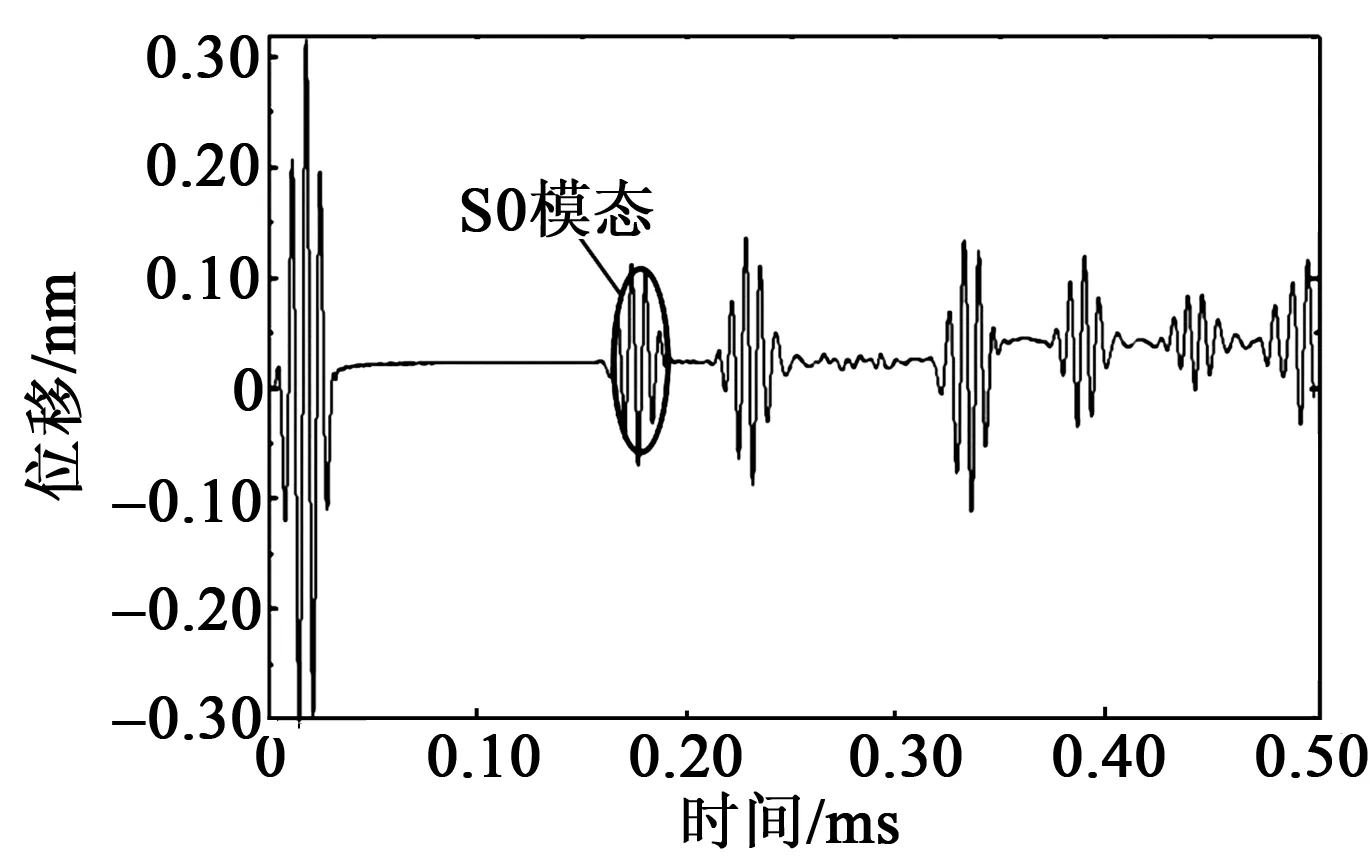
圖15 觀測點A處的Lamb波傳播圖
用S0模態來計算傳播時間,查詢數據點得t=155.97 μs,由S=v·t/2可得S=398.84 mm,與實際位置400 mm很接近。充分驗證了本次仿真的可行性,為實驗部分奠定基礎。
4 結束語
通過研究Lamb波的頻散特性,利用ABAQUS建立Lamb波在缺陷鋁板中傳播的模型并進行分析求解,在尺寸為400 mm×400 mm×4 mm的鋁板中識別處出了鋁板缺陷大小為12 mm×8 mm的位置并與實際位置進行對比,誤差值在5 mm以內,確定了此次仿真的有效性和準確性。充分驗證了利用橢圓法對鋁板損傷定位識別的有限元模擬的可行性。

