基于自校正PID控制的智能懸臂梁振動控制

胡曉琳，張 婷

（上海工程技術大學 機械與汽車工程學院，上海201620）

近年來，壓電傳感器和致動器結合的智能懸臂梁系統引起了許多研究者的關注[1]，同時基于智能系統振動控制的控制器設計也引起了學者們廣泛的關注[2]；特別地出現了大量關于應用壓電材料抑制智能懸臂梁系統振動的控制器設計[3–4]。Zhu 等[5]提出了采用自適應前饋控制方法對壓電智能懸臂梁進行主動振動抑制；Zhang等[6]將自適應極點配置控制理論應用到在熱環境下的智能懸臂梁的振動控制中。但將傳感與致動一體化的壓電材料應用于懸臂梁系統的研究不多。而且，目前許多研究人員致力于通過各種控制方法控制智能懸臂梁的振動，Koofigar等[7]提出了采用自適應控制方法對模型不確定性和環境擾動的智能結構進行振動抑制；Zhang等[8]實現了時滯智能梁遲滯模型的構建，并且采用自適應振動抑制方法實現了其在控制系統中的應用；但應用壓電雙晶片進行系統參數辨識實現實時振動控制的設計并不多見。

鑒于目前研究現狀，本文通過假設模態法和哈密頓原理建立了智能懸臂梁的動力學模型[9]；再基于智能懸臂梁的動力學模型，采用自校正PID控制[10–12]和普通PID 控制，實現智能懸臂梁的自由振動控制的理論仿真與實驗驗證。因此，為使智能懸臂梁自由振動得到有效控制，本文基于壓電雙晶片的致動與傳感一體化特性，通過采用自校正PID 控制方法與基于Neigler-Nicholes參數整定法的普通PID控制方法，得到智能懸臂梁主動控制的數值仿真與實驗結果，再對此2種控制方法的控制結果進行對比，得出了自校正PID控制的效果更為顯著和更為有效的結論。

1 智能懸臂梁系統

1.1 壓電雙晶片

如圖1 所示為壓電雙晶片實物圖，壓電雙晶片的構造層為三層，其中，中間層為電極片，上下層均為壓電晶片，電極片和壓電晶片之間通過膠粘方式聯接[13]。

圖1 壓電雙晶片實物圖

如圖2 所示為壓電雙晶片結構簡圖，左側為固定端，右側為自由端，當上層為驅動層，下層為傳感層時，對驅動層施加一電壓，它的自由端可彎曲產生位移，位移的幅度和方向與施加的壓電具有函數關系；此時下層會因為上層的驅動力而發生縱向變形，即傳感層會輸出傳感電壓。

圖2 壓電雙晶片簡圖

壓電雙晶片相對于其他壓電材料的優勢在于它輸出位移大，反應速度快，適合慣性沖擊精密驅動場合；并且將傳感與致動兩個功能結合在一起，從而減少了元件的數量。

1.2 智能懸臂梁結構

根據前人[14]的研究，對于1 階模態振動，當壓電片的位置越靠近固定端，振動衰減速度越快；對于2階模態振動，當壓電雙晶片處于距懸臂梁中部某一位置時，具有較好的綜合控制性能，若同時考慮1、2階模態的控制時，壓電片位于懸臂梁固定端或中部某一位置時，具有相近且較好的控制性能，通過實驗亦可驗證：當壓電片處于智能懸臂梁中間偏左處時控制效果更好。如圖3 所示為智能懸臂梁結構圖，當智能懸臂梁右側的自由端受到外部擾動時，利用壓電雙晶片的驅動特性控制懸臂梁自由振動，同時利用壓電雙晶片的傳感特性獲取相應位置的輸出位移，從而實現智能懸臂梁振動控制閉環回路。

圖3 智能懸臂梁

2 智能系統的動態模型

2.1 智能懸臂梁動力學模型

本文所研究的對象為理想的均勻懸臂梁，沿梁長度x方向變化的抗彎剛度為EI(x) ，梁的質量密度為ρ,單位長度質量為m(x) ，作用在梁上的橫向荷載為P(x,t)，梁的橫向位移（撓度）w(x,t)為隨坐標x和時間t連續變換的函數。

本智能懸臂梁系統的方程[15]如下

式中：CP為壓電片電容，單位法拉；

EP為壓電傳感器的彈性模量；

b為懸臂梁的寬度；

tb為懸臂梁的厚度；

e31為壓電系數；

w為柔性臂的撓度（臂的橫向位移）。

但是此系統致動方程為1 階偏微分形式，被控制量w（撓度）既是時間的函數，同時又是空間的函數，對此，采用正交模態變換，將偏微分方程形式轉換成一組2階微分方程形式，從而便于設計控制器。

對于單自由度智能懸臂梁系統而言

式中：w(x,t)是體系的幾何位移坐標；

?(x)是第n階振型的振型函數；

q(x)是第n階振型的廣義坐標，也稱振型坐標。

傳感方程的模態變換如下，將式（2）代入壓電傳感方程式可得

致動方程的模態變換如下，當取?(x)為正則振型，Mi=1，所以，梁的振動微分方程為

本小節對粘貼有壓電雙晶片的智能懸臂梁建模問題進行了研究，采用模態分析方法，利用模態振型正交性，將系統的偏微分方程形式轉換為一組2 階微分方程形式。動力學模型是控制系統的對象，所建模型為之后的控制器的設計奠定了基礎。

2.2 智能懸臂梁的狀態空間描述

狀態空間描述，是現代控制理論的基本出發點。將式（4）描述的壓電雙晶片智能懸臂梁用矩陣的形式表示為

式中：ψ11=?'1(x2)-?'1(x1)

取此系統狀態為

輸入為

則整個閉環系統的描述為

即

取60

3 控制器的設計

3.1 自校正PID控制器設計

3.1.1 系統參數辨識

最小二乘法由于具有原理簡明、收斂較快、易于理解、易于編程實現等特點，在系統參數估計中應用廣泛。本文采用遞推最小二乘法[16]解決對象參數在線實時估計的問題。

已知：na、nb和d。

(2)采樣當前輸出y(k)和輸入u(k)；

(4)k →k+1，返回第2步，繼續循環。

由遞推最小二乘法系統參數辨識，獲取自校正PID控制器所需的參數a和b。

3.1.2 自校正PID控制器設計

本文采用自校正PID控制抑制智能懸臂梁的自由振動。其主要思想是尋求一個反饋控制率，使得閉環傳遞函數的極點位于期望的位置上。圖4所示為間接自校正PID 控制的系統結構，通過在線實時辨識得到系統參數，再根據自校正PID 控制的參數變化來實現期望的輸出，以提高系統的穩定性、響應速度和控制精度。

以下為自校正PID控制器[16]的設計過程。

設被控對象為

式中：u(k)和y(k)表示系統的輸入和輸出，e(k)為外部擾動，d?1為純延時，且

對式(13)所示系統采用PID控制，為消除常值干擾，控制器必須有積分作用，此時，對應的PID 控制器可表示為

式中

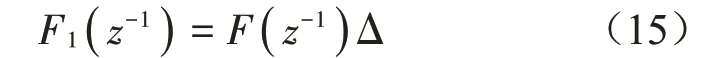
且

圖4 間接自校正PID控制

將式（14）代入式（13）得閉環系統輸出為

令閉環特征多項式為期望傳遞函數分母多項式，即

式中：對于Am的選擇仍需滿足極點配置控制（PPC）中相應的相容性條件。

結合式（15），上式又可表示成

為保證式（18）有唯一解，令ΔAF和z-dBG的階次相同（已知degΔA=3、degG=2），且等式右邊階次小于左邊階次，即各多項式的階次需滿足下列關系：

則Diophantine 方程式（18）中多項式F、G 可用MATLAB函數diophantine.m進行求解。

3.2 普通PID控制器設計

為了與自校正PID 控制效果對比，本文還采用了Ziegler-Nichols參數整定方法[17]確定比例增益KP、積分時間TI、微分時間TD這3 個參數，以實現普通PID控制器的設計。

通過實驗方法，根據階躍響應信號可近似確定參數K(靜態放大系數)、L(容量滯后時間)和T(時間常數)，然后再根據表1 確定普通PID 控制器的有關參數。

表1 齊格勒-尼柯爾斯調整法則

4 仿真和實驗驗證

4.1 仿真驗證

基于自校正PID 控制和普通PID 控制理論，本文應用MATLAB/SIMULINK 對智能懸臂梁實現振動控制的理論仿真與分析。

圖5所示為普通PID控制框圖：基于智能懸臂梁動力學模型，應用Ziegler-Nichols 參數整定方法，得出了普通PID 控制器參數，其中包含比例增益KP=20.00，積分時間TI=2×10-6，微分時間TD=5×10-7。

圖5 普通PID控制之SIMULINK控制模塊圖

圖6為自校正PID控制框圖：針對智能懸臂梁動力學模型，應用MATLAB/simulink 的function 模塊編程功能，采用自校正PID控制方法，實現智能懸臂梁的振動控制研究。

圖6 自校正PID控制之SIMULINK控制模塊圖

圖7（a）為仿真中普通PID控制下的控制電壓隨時間變化的結果圖，圖7（b）為該控制下系統的輸出位移與未控制下的自由振動位移隨時間變化的結果對比圖。由圖可知，其仿真中控制效果并不明顯。

圖8（a）為仿真中自校正PID控制下的控制電壓隨時間變化的結果圖，圖8（b）為該控制下系統的輸出位移與未控制下的自由振動位移隨時間變化的結果對比圖。仿真中的控制效果較明顯，與普通PID控制的仿真結果相比，自校正PID 控制能夠更明顯且更有效地控制智能懸臂梁。

4.2 實驗驗證

合編程軟件環境下的自校正PID 控制器或普通PID控制器進行處理，把得到的0～10 V 控制電壓傳輸到數據采集卡，之后通過HPV系列壓電陶瓷驅動電源放大15倍后產生相應的抑制力，加載到壓電雙晶片，實現對懸臂梁的振動抑制。

首先，為了減少實驗誤差，在進行實物實驗之前，對實驗設備進行檢查和調試，即檢查設備是否可以正常運行，調試各個設備輸出與輸入的情況，觀察是否可達到實驗所要求的標準。其次，運行由labVIEW和MATLAB混合編程軟件；然后給智能懸臂梁施加一組干擾并觀察其相關曲線的運行軌跡；最后收集實驗數據，并對數據進行處理和分析，得出結論。

圖10（a）為實驗中普通PID 控制下的控制電壓隨時間變化的結果圖，圖10（b）為該控制下系統的輸出電壓與控制前自由振動的輸出電壓的結果對比圖，實驗結果表明其控制效果并不明顯；圖11（a）為實驗中自校正PID控制下的控制電壓隨時間變化的結果圖，圖11（b）為該控制下系統的輸出電壓與控制前的自由振動的輸出電壓的對比圖，結果表明，在系統運行初期，系統需要一定時間進行估計參數，故存在較大幅度的振蕩；一段時間之后，該系統具有較好的控制效果，在0.8 s 后，輸出電壓的幅值均減小到較小值，與無控制的自由振動相比，實驗中的控制效果較明顯，由此可知自校正PID 控制方法具有較好的輸入跟蹤能力和自適應能力，與普通PID 控制相比，自校正PID控制在抑制自由振動方面更為有效。

圖9 所示為智能懸臂梁振動控制系統實驗平臺，由HPV 系列壓電陶瓷驅動電源、MCC-USB 1808X 以及裝有labVIEW 和MATLAB 的電腦組成。利用labVIEW、MATLAB 混合編程技術，采用MATLAB語言編寫相應的控制程序，構成實驗軟件系統。labVIEW所搭配的控制器用于實現對振動信號的分析和處理。HPV系列壓電陶瓷驅動電源是一種為壓電陶瓷致動器設計開發的高品質驅動電源，能夠為壓電陶瓷提供高穩定性、高分辨率的電壓，并且有優良的頻率響應和極低的靜態紋波。信號的傳輸與轉換采用數據采集卡，MCC-USB 1808X數據采集器提供18位高分辨率同步模擬輸入通道，同時具有數字I/O和計數器功能，其體積小，縮減了實物實驗空間；本身便捷的USB 連接方式，使操作便捷且高速，削減了成本，縮短了時間，提高了實驗效率；同時自身的高速傳輸與轉換速度較快的特性保證了振動信號處理的及時性。

當懸臂梁的自由端受到干擾后，壓電雙晶片采集應變，傳感信號經MCC-USB 1808X 數據采集卡轉換處理后，傳至電腦，由labVIEW 和MATLAB 混

圖7 普通PID控制之控制電壓和控制后與控制前輸出位移對比（仿真）

圖8 自校正PID控制之控制電壓和控制后與控制前輸出位移對比（仿真）

圖9 實驗平臺

5 結語

本文通過應用假設模態法和Hamilton原理構建智能懸臂梁的動力學模型；再基于智能懸臂梁的動力學模型，采用自校正PID控制和普通PID控制，實現了智能懸臂梁的自由振動控制理論仿真與實驗驗證。然后通過SIMULINK 和實驗平臺，分別得到了采用壓電雙晶片的智能懸臂梁主動控制的數值仿真與實驗結果，再對此兩種控制方法的控制結果進行對比，得出了自校正PID 控制的效果更為顯著的結論。這為基于自校正PID 的控制方法，采用壓電雙晶片對智能結構吸振減振提供了理論與實驗研究的基礎。

圖10 普通PID控制之控制電壓和控制后與控制前輸出位移對比（實驗）

圖11 自校正PID控制之控制電壓和控制后與控制前輸出位移對比（實驗）