基于頻響函數的結構損傷識別模型修正方法

殷 紅，馬靜靜，董小圓，彭珍瑞，白 鈺

（蘭州交通大學 機電工程學院，蘭州730070）

模型修正在復雜工程結構的損傷識別中有著非常重要的作用。目前設計參數型有限元模型修正（Finite element model updating，FEMU）方法應用廣泛，主要有基于頻響函數（Frequency Response Function，FRF）的模型修正和基于模態參數的模型修正[1]。和后者相比，基于FRF 的FEMU 不需要模態識別，避免了在模型修正過程中引入識別誤差，并且FRF能夠提供更多的數據，適用范圍更廣[2]。

在模型修正中建立靈敏度方程時，要求實測自由度數等于有限元模型的自由度數，而通常實測自由度數遠遠少于有限元模型的自由度數，這就導致有限元模型與試驗所測的自由度數目不匹配。通常用試驗模態擴展方法[3]和有限元模型縮聚方法[4]來解決此問題，然而這些方法往往會讓有限元模型修正變成非線性優化問題[5]。為了得到準確的結果，建立線性靈敏度方程是非常需要的。文獻[6]用損傷結構的固有頻率近似計算未測量的FRF 數據。此外，目前把模型修正與損傷識別相結合的方法引起了學者的廣泛關注。文獻[7]用模型修正理論對橋墩進行損傷定位與定量評估。文獻[8]提出了一種基于FRF 模式置信準則的改進模型修正方法，用以識別結構的損傷指數。

FEMU 的結果往往受多種因素影響，除了建立準確的靈敏度方程外，測點位置的選擇也是FEMU必須解決的關鍵問題，而且，選擇合適的頻率范圍也對FEMU 的結果有著重要影響。基于此，本文用FRF 攝動分析法建立FRF 靈敏度方程，研究如何選擇頻率范圍以及解決測試信息不完備問題，然后提出針對于頻響函數模型修正的傳感器優化布置方法，確定傳感器的數目和位置，最后通過給桁架結構設定損傷工況來驗證該模型修正方法的有效性。

1 基于頻響函數的模型修正方法

1.1 位移頻響函數

一個具有比例阻尼的多自由度系統，激勵向量為f，位移響應向量為x。在外部激勵作用下的運動微分方程可以表示為

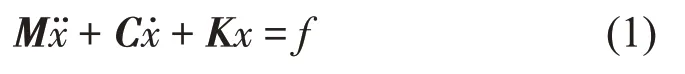
式中：M、K和C分別表示質量矩陣、阻尼矩陣和剛度矩陣。對式(1)進行傅里葉變換，可得

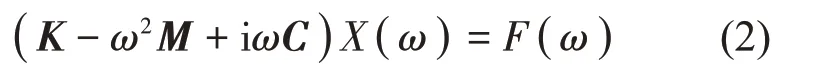
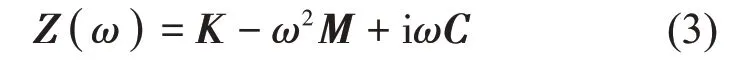
Z(ω)的逆矩陣即為位移頻響函數矩陣

則位移頻響函數即為響應與激勵傅氏變換之比

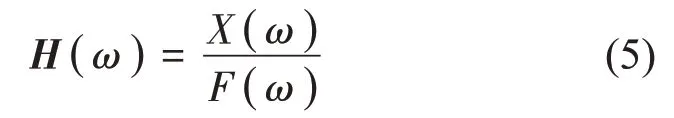
位移頻響函數可以寫成如下模態疊加的形式，從而可以通過系統模態參數來計算頻響函數。

式中：ωg為第g階無阻尼固有頻率；ξg為模態阻尼系數；?gp和?gq分別為第g 階模態在節點p 和節點q 的振型幅值；Hpq(ω)為頻響矩陣H 的第(p,q)元素，表示在第q自由度施加簡諧激勵時，第p自由度上的位移響應；r表示模態數目。

1.2 基于頻響函數攝動分析的模型修正

利用結構實測頻響函數和有限元計算得到頻響函數間的差值構造如下目標函數

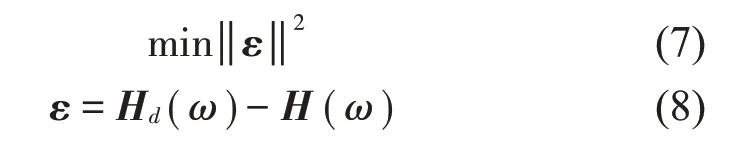
式中：ε 和Hd(ω)分別為測量得到的結構位移頻響函數和根據有限元分析得到的位移頻響函數；ε 為頻響函數殘差向量。

當結構出現損傷時，結構特性和響應會隨之發生改變，為了避免由對頻響函數的求導和運用1 階泰勒級數所引起的復雜運算，用攝動法建立靈敏度方程，損傷結構位移響應的傅里葉變換為

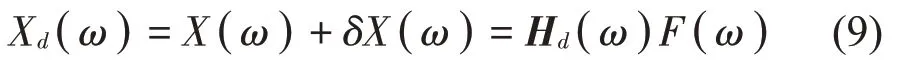
損傷結構的頻響函數矩陣為

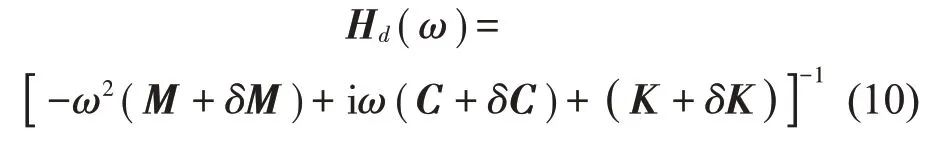
式中：δM、δC 和δK 分別表示損傷結構質量、阻尼和剛度矩陣相對于完好結構的攝動量。

將式(10)代入式(9)可得

將上式展開并從中求出δX(ω)，得到

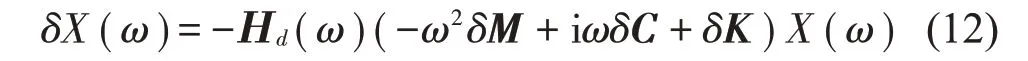
將式(5)和式(9)代入式(12)，并消去F(ω) ，可得

式(13)可準確地修正結構質量和剛度參數，因為它實質上是一個關于結構參數變化量的線性函數。目前大多數阻尼模型不能很準確地去模擬實際阻尼效應，反而會增加模型誤差，影響模型修正結果，所以本文中不對阻尼參數進行修正。

其中，結構總體剛度矩陣的變化可由各剛度修正單元的偏微分之和來表示

同理，結構總體質量矩陣的變化表示如下

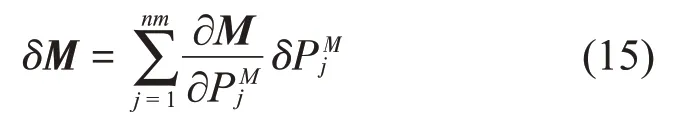
將式(14)、式(15)代入式(13)，并忽略對阻尼參數的修正，即δC=0，可得

式(16)可以改寫為如下矩陣相乘的形式

式中：δPM為質量參數靈敏度矩陣，δPS為剛度參數靈敏度矩陣。δPM和δPS分別為質量參數和剛度參數的變化量，δP 為所有修正參數的變化量。S(ω)表示總體靈敏度矩陣。

在實際測試中，方程組(17)通常是不適定的，其最小二乘解為

式中：S+=[S(ω)TS(ω)]-1S(ω)T。最小二乘法的解主要由數值系數較大的部分方程決定，也就是說有些方程可能會掩蓋其他方程的信息。所以，通常選用適當的正則化方法來減小靈敏度矩陣的條件數[9]，進而降低靈敏度矩陣的病態性，減少其對模型修正結果的影響。本文中采用相應行的2-范數對靈敏度矩陣的每一個行向量進行歸一化。

1.3 估計損傷結構的FRF

由式(13)建立模型修正的靈敏度方程時，要求實測自由度數等于有限元模型的自由度數，而通常實測的自由度數遠遠少于有限元模型的自由度數。

圖1 是結構在完好和損傷狀態下的FRF 曲線，從圖中可看出當激勵頻率位于結構的共振區周圍時，損傷將導致FRF沿著坐標軸有一定的移動，但形狀并沒有發生明顯的改變。分析表明，在不同的共振區完好狀態FRF曲線與損傷狀態FRF曲線的平移距離不同。因而可以先測量各共振區內的平移量，再將完好狀態FRF曲線通過平移得到損傷狀態FRF曲線的近似估計。

因此，在共振區附近Hd(ω)的近似估計可表示為

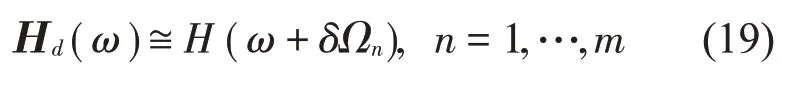
其中

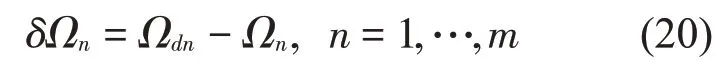
式中：Ωdn和Ωn分別為完好結構和損傷結構的第n階固有頻率，δΩn表示完好結構和損傷結構間的頻率變化量，m表示測量得到的損傷結構固有頻率的階數。圖1顯示了這種估計的過程。

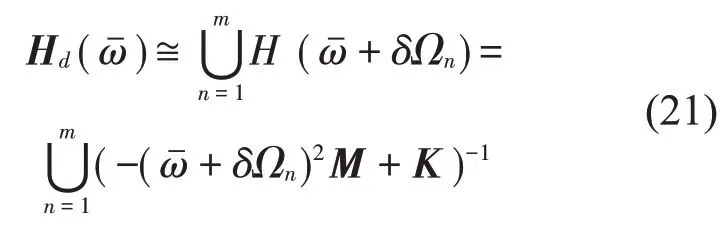
建立靈敏度矩陣時用的是無阻尼的H(ω)和估計得到的Hd(ω)，但是為了模擬阻尼對算法的影響，用有阻尼的Hd(ω)和無阻尼的H(ω)來計算殘差向量ε。在之后的迭代計算中，完好結構的結構參數將不斷地更新，逐漸趨近于損傷結構的參數，因而，式(19)和式(20)中，初始Ωn和H(ω)將不斷迭代更新，向損傷結構的固有頻率和頻響函數不斷收斂。

圖1 結構在完好和損傷狀態時第n階固有頻率附近的FRF

2 模型修正頻率范圍選擇

頻率的合理選擇能提高有限元模型修正的精度和收斂性。圖2 是在整個頻率范圍內，結構受到激勵時所有測點自由度響應的靈敏度矩陣的2-范數圖。范數的值越大，表明結構參數發生變化時，其FRF的靈敏度越高。

圖2 完整頻率范圍內結構單點激勵時所有測量點靈敏度矩陣的2-范數

從圖2 可以看出，結構的FRF 在遠離共振頻率時對結構參數的變化不敏感，而在共振頻率附近具有良好的靈敏度，所以選共振頻率附近的頻率點進行模型修正。

本文沒有對阻尼參數進行修正，所以要減小結構阻尼對模型修正結果的影響。由于阻尼在共振區內對振幅的影響很大，當遠離共振區時影響迅速減小，因此所選擇的頻率范圍應與共振點保持一定距離，在每次迭代中，始終排除共振點周圍約4 Hz 以內的頻率范圍。

若2 個相鄰的共振峰距離太近，則其之間的頻段內不能保證FRF 的變動量在修正過程中單調下降，因而排除該區域，以避免振幅非線性問題[10]。在每次迭代時，頻率范圍還需根據共振點的變化進行調整。

3 模型修正測點選擇

在模態測試及模型修正中，有效獨立法（Effective independence，EFI）被廣泛應用于確定傳感器測點。后來，Kammer[11]提出了頻率響應有效獨立 法（Frequency effective independence，FEFI）。FEFI的主要步驟如下：

(1)在目標頻率范圍內，利用有限元分析得到結構固有頻率和振型計算頻響數據矩陣

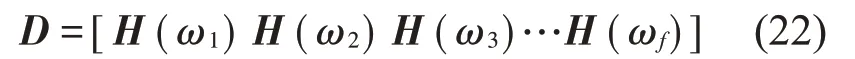
式中：H(ωi)∈Cns×na為頻率ωi處的頻響矩陣，i=1，2，…，f 表示采樣頻率點，f 為頻率點總數，ns和na為傳感器數目和激勵點數目。

(2)對頻響數據矩陣進行奇異值(SVD)分解，對模型進行降維和去噪。D經SVD分解后表示為

式中：U 是一個ns×ns維的復正交矩陣，它相互正交的列向量也稱為主方向；S 是由奇異值組成的對角矩陣；V是一個na×na維的復正交矩陣，它的行向量表示相應主方向上歸一化的頻率響應。頻響矩陣的各主方向同時滿足

式中：U∈Cns×na和V ∈Cns×na為酉矩陣，對角陣S 對角線上的元素即為奇異值。U相互正交的列向量也稱為主方向；V 的行向量表示相應主方向上歸一化的頻率響應。頻響矩陣的各個主方向滿足關系。式中：上標*表示共軛轉置。由于奇異值的大小反映了系統的總能量在相應主方向上的分布，因此，將奇異值按降序排列，去除接近于0的奇異值，進行主成分分析，保留占系統總能量95%～99%的主分量，實現降維和去噪，同時保留系統中的真實模態信息。

設 U=[u1,u2,…,uns]，V =[v1,v2,…vna]T，S=diag(σ1,σ2,…,σr,0,…,0)。其中，us∈Cns×1，σi是D的奇異值，若選前l 個分量進行重構，則H 可近似表示為

式中：DD為D的主分量。

(3)根據主成分分析，將U中保留主方向的列向量組成的矩陣記為ψ。參照EFI，頻響數據矩陣可表示為主方向上的頻率響應與獨立同分布高斯白噪聲的和。記高斯白噪聲為N，則有

其中：ψ表示相應主方向上的頻率響應。根據Fisher信息矩陣推導可得

以信息矩陣的行列式作為目標范數，計算有效獨立分布向量

ED中越小的元素表示對應的候選測點對目標模態分量線性獨立性的貢獻越小，應該首先剔除，依次迭代，直至候選測點數目為所需要的傳感器數目為止。

由文獻[12]可知，采用EFI 選擇測點時，若傳感器數目大于目標模態數目，測點可能在局部聚集，從而導致信息冗余。由于FEFI 是EFI 在頻域內的推廣，具有與EFI 相同的性質，因此，分兩步為模型修正選擇測點位置。首先采用FEFI 確定與主方向相等數目的測點位置；然后采用文獻[13]中的距離系數—有效獨立法，確定傳感器的數目。該方法以距離系數修正Fisher信息矩陣，避免了EFI中信息冗余的問題。迭代中以使修正后的Fisher信息矩陣行列式最大化來逐步增加傳感器布置節點，直到布置的傳感器采集的信息能夠得到可靠的模型修正結果。

算法的流程如圖3所示。

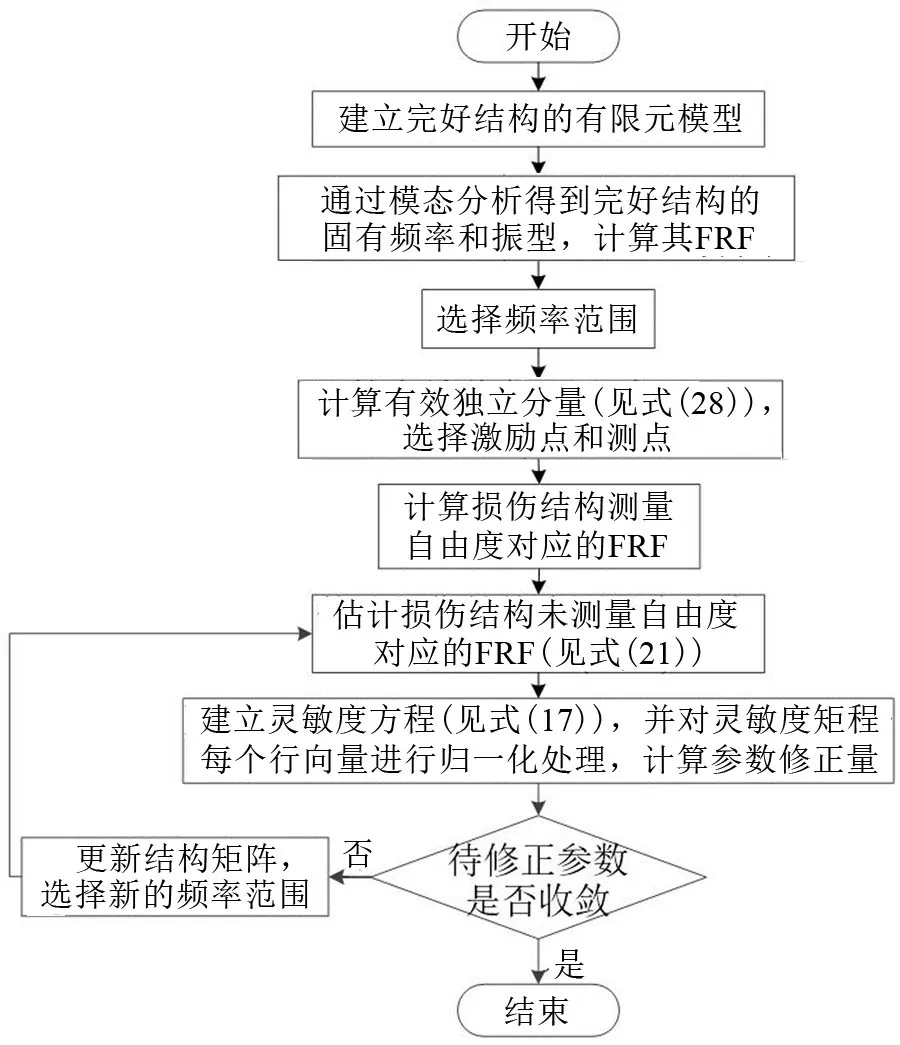
圖3 模型修正流程圖

4 數值模型試驗

4.1 模型簡介

圖4 桁架結構的單元及尺寸/cm

圖4所示的平面桁架結構由40 個桿單元組成。每個桿單元的密度為7 800 kg/m3，彈性模量為200 GPa。1－9號單元、10－18號單元、19－26號單元以及27－40號單元的橫截面積分別為18 cm2、15 cm2、10 cm2和12 cm2。結構有18 個節點，33 個自由度，如圖5所示。

圖5 桁架結構的自由度

這里用0.5%的阻尼系數來模擬模型的實際阻尼，選擇單元軸向剛度EA 作為待修正參數，E 為彈性模量，A為橫截面積。設定2種損傷工況來驗證模型修正方法的有效性，在工況1中，預設第7、10、17、23 和30 號單元為損傷單元，其剛度分別下降20%、20%、20%、30%和30%；工況2中，預設第15、25和38 號單元為損傷單元，軸向剛度分別下降30 %、40%和30%。假設結構受單點激勵，激勵點分別選擇在第2、16、19、29 和33 自由度處。對以上2 種損傷工況進行有限元分析，得到損傷結構的固有頻率和頻響函數。

4.2 選擇頻率范圍并估計損傷結構的FRF

分別對完好結構和損傷工況1 這2 種工況下的結構在第2 自由度處進行激勵，第13 自由度上采集輸出信號，分析得到無阻尼頻響函數曲線如圖6所示。

圖6 結構在完好狀態和損傷工況1對應的FRF

可以看出，在共振區完好結構和損傷結構的頻響函數差異變大，再結合第2小節的規則，模型修正的頻率選擇為共振區附近的頻率點。去除含有前3個共振區的低頻段；為避免振幅非線性的問題，忽略第5和第6共振區之間以及第7和第8共振區之間的頻率點。

選取結構的前8階固有頻率，根據以上分析，采樣間隔為1 Hz，工況1和2中分別選擇的頻率范圍如表1所示。

表1 用于模型修正的頻率范圍

根據上面選擇的頻率，采用1.3小節的方法對相應的FRF 進行估計。圖7 為損傷工況1 下結構的精確FRF曲線以及在所選頻段內估計的FRF圖。從圖7 中可以看出FRF 的估計值高度近似于FRF 的精確值。

圖7 工況1下精確的FRF以及在所選頻段內估計的FRF

4.3 測點優選

根據FEFI的算法思想，分兩步完成測點優選。

第一步，初選感器布置位置。

根據4.2 小節確定的頻率范圍計算頻響數據矩陣D。對D 進行SVD 分解，降維后保留前5 個奇異值，讓主方向上的能量占到系統總能量的95%。由式(28)計算有效獨立分布向量,在迭代中逐次剔去其中最小元對應的候選測點，直至候選測點減少至5個時停止。迭代結束時確定初選測點為第3、10、17、19、33自由度。

為了和采用距離系數—有效獨立法優化測點位置后的效果相比較，在進行下一步之前，在此先取初選測點進行模型修正，得到結構損傷識別結果。

針對工況1，在這5 個初選自由度上布置傳感器，進行基于FRF 的FEMU，損傷識別結果如圖8所示。

由圖8 可看出，對第7、10、17、30 單元的損傷識別較準確，對第23 單元處的損傷程度識別較差，同時對第5、20、21、22、33 等單元處出現了損傷誤判。說明在初選測點下直接進行模型修正雖然可以對大多數實際損傷位置進行識別，但同時會在其他位置上出現誤判斷和欠判斷的情況。由于損傷識別結果不能很好地反映實際工況，在此不再對工況2 進行試驗。

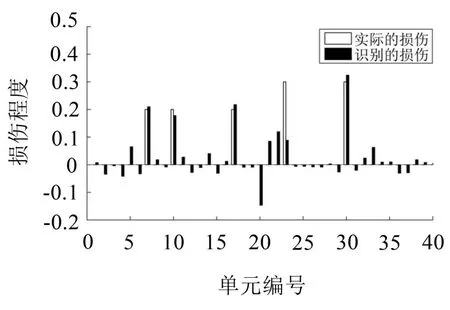
圖8 布置5個傳感器時模型修正識別的損傷和工況1實際損傷

第二步，采用距離系數—有效獨立法增加測點位置。

為了改善損傷識別效果，可逐步增加結構中布置的傳感器數目，并采用距離系數—有效獨立法確定增加的測點位置，得出第6 個測點位置為第25 自由度。針對工況1和工況2，分別在第3、10、17、19、25、33自由度處布置傳感器，進行基于FRF的FEMU，損傷識別結果如圖9所示。

4.4 模型修正結果分析

從圖9可以看出，布置6個傳感器時獲得的頻響數據能識別出工況1和2的損傷程度和位置，且識別結果較為準確。雖然在一些位置出現了虛假損傷，但都很微小，可以忽略不計。這主要是受阻尼和模型修正中估計誤差的影響而導致的。

表2 給出了彈性模量的修正結果。可看出，修正后損傷單元的彈性模量和真實值高度吻合，修正結果相對誤差的最大值為2.58%。

表3給出了兩種損傷工況下固有頻率的修正結果。可以看出，修正后的結構前8 階固有頻率和通過有限元分析計算得到的精確值基本一致，最大相對誤差僅為0.33%。說明采用本文方法能有效地識別出損傷結構的真實參數，可以提高結構動力學分析的準確性，為后續的優化設計提供依據。

5 結語

(1)建立數學模型時采用攝動法進行靈敏度分析，推導出質量和剛度參數變化與FRF 變化之間的線性關系。避免了使用泰勒展式以及對頻響矩陣的求導運算，而且建立的模型修正方程沒有截斷誤差，在參數修正過程中穩定性良好。

(2)分析完整頻率范圍內結構單點激勵下所有測量點靈敏度矩陣的2-范數，合理確定用于模型修正的頻率范圍。利用測量得到的損傷結構的固有頻率和完好結構的FRF 來重構未測量節點上的FRF，解決了測試信息的不完備問題。對靈敏度矩陣的每一個行向量采用相應行的范數進行歸一化，提高了算法的穩定性。

圖9 布置6個傳感器時模型修正識別的損傷和實際損傷

表2 彈性模量修正結果

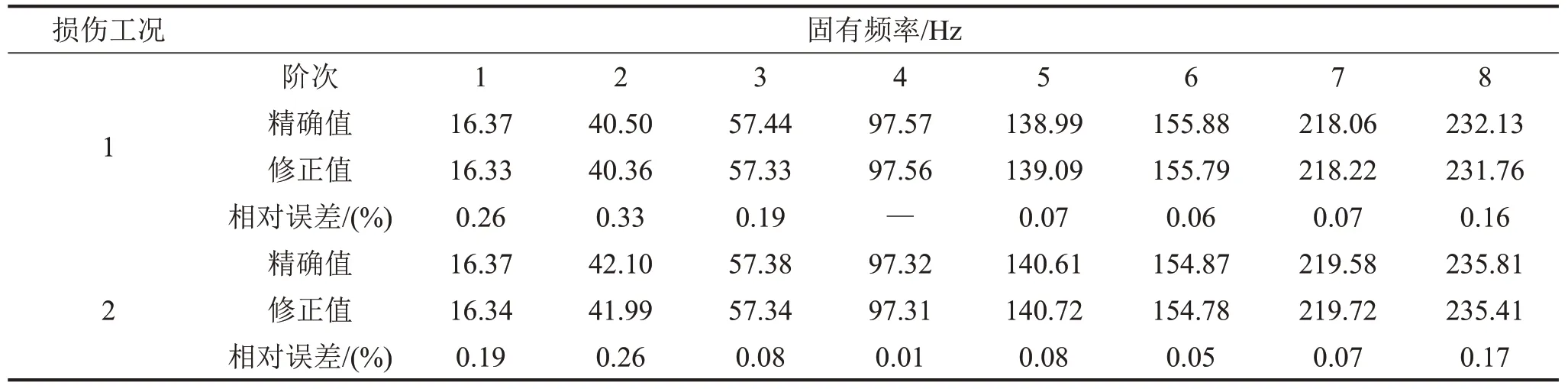
表3 2種損傷工況下結構固有頻率的精確值及修正值

(3)測點的優選決定了損傷識別的精度。采用FEFI 與距離系數—有效獨立法相結合的方法來確定傳感器布置方案。數值模型試驗分析表明，由該方法確定的少量傳感器獲得的FRF數據就能較為準確地識別損傷，模型修正結果與損傷結構真實參數高度吻合。

雖然數值算例中得到了較為理想的修正結果，但是實際試驗中存在環境等不確定性因素，所以，需要進一步研究如何利用實測數據并考慮不確定因素進行模型修正。