縫縮量、袖山高及裝袖角度的定量關(guān)系研究

沈德垚，侯東昱

(1.河北科技大學(xué) 紡織服裝學(xué)院，河北 石家莊 050000；2.河北省紡織服裝工程技術(shù)研究中心，河北 石家莊 050000)

目前國內(nèi)學(xué)者在裝袖縫縮量方面對面料與縫縮量的關(guān)系及對縫縮量的分配進行了深入的研究分析，劉東[1]就織物性能與袖子縫縮量的大小關(guān)系做了較為細致的討論，用數(shù)值分析的方法分析出了面料厚度與縫縮量的定量關(guān)系，并探討了縫縮量的分配方法和裝配位置的確定方法；卓開霞[2]提出了軸線配袖法，以合體袖的縫縮量及袖山高的相關(guān)變化為基礎(chǔ)，應(yīng)用數(shù)學(xué)分析方法設(shè)計實驗對縫縮量與袖山高及袖窿弧線的增量進行回歸分析，得出這3個相關(guān)變量的回歸方程。目前對裝袖角度與其相關(guān)變量的研究還停留在定性研究階段。想要根據(jù)不同的著裝條件設(shè)計出符合需求的不同裝袖，定性分析已不足以滿足不斷變化的著裝需求，因此，對裝袖中結(jié)構(gòu)變量的定量分析有一定的現(xiàn)實意義。

1 裝袖縫縮量及裝袖角度

1.1 縫縮量的產(chǎn)生

肩端點與大臂之間通過一個半球型曲面圓順連接，衣袖的袖山高一般覆蓋上臂圍線與肩點之間球面的最大曲線的長度，通過對袖山弧線與袖窿弧線的差量進行抽褶，做出臂根的曲面造型，還原出人體臂根形態(tài)，使裝袖達到飽滿立體的效果，袖山頭弧線通過抽褶去掉的長度量就是縫縮量[3]。這個量隨衣袖的寬松程度、袖斜線傾角、面料性質(zhì)變化而改變[4]。

1.2 縫縮量的作用

袖山縫縮量主要有功能性和設(shè)計性2個方面的作用，首先，在功能性方面，肩關(guān)節(jié)是肱骨頭與肩胛骨關(guān)節(jié)窩相連接的多軸性球關(guān)節(jié)，在身體運動中可動范圍最大[5]。考慮人體手臂頂部的球冠狀結(jié)構(gòu)形態(tài)的同時需要兼顧手臂前伸，后揚以及上抬等基本活動動作，因此必須通過工藝收縮來滿足人體肩部及臂部的基本活動需求，以更好地符合上肢頂部凸勢的表面形狀[6]。其次，考慮到裝袖工藝特點，裝袖與衣身之間的縫份量在袖山弧線長于袖窿弧線時向衣袖方向傾倒。袖山弧線輪廓呈現(xiàn)出圓弧形，目的是避免縫份向外撐起，通過縮縫的工藝手法達成這種圓順美觀的效果[7]。袖部造型作為服裝設(shè)計的重要部位，通過工藝收縮來達到袖山圓順而挺翹的外觀特點，以符合人們對優(yōu)美袖型的審美認(rèn)知。

1.3 縫縮量的設(shè)計

縫縮量的設(shè)計受面料種類、款式結(jié)構(gòu)以及制作工藝等因素影響。輕薄面料在裝袖縫合時易出現(xiàn)無法熨平的死褶，對縫制工藝要求較高，因此縫縮量需要相應(yīng)地減小以滿足形態(tài)及縫制需求。厚重面料需要相應(yīng)加大縫縮量，以使袖山處飽滿圓潤。縫縮量需要根據(jù)所設(shè)計服裝的面料及款式結(jié)構(gòu)工藝來進行調(diào)整，通常有2種調(diào)整方法，一種是控制袖山高不變，調(diào)整袖肥的長度；另一種是控制袖肥不變，調(diào)整袖山高的長度并調(diào)整前后袖山弧線的抬升量，最終使縫縮量長度達到符合需求的值。

1.4 縫縮量的影響因素

影響袖山造型的因素很多，如面料厚度、版型設(shè)計、制作工藝、服裝款式風(fēng)格及裝袖角度等[8]。袖子的縫縮量隨面料的厚度增加而增加，而袖山高和縫縮量則有著線性關(guān)系[9]。本文主要通過控制袖肥不變，設(shè)計實驗得出一定條件下袖山高與縫縮量及裝袖角度之間的定量關(guān)系，分析其變化曲線找到一般性規(guī)律，以便更好地提高袖型設(shè)計的實用性和美觀性。

1.5 裝袖角度

當(dāng)穿著者處于靜止站立時，衣袖呈現(xiàn)自然垂落狀態(tài)，將手臂沿身體側(cè)平面進行軸向抬升，此時手臂與鉛直方向的夾角就是裝袖角度。裝袖角度受袖山高和縫縮量的變化影響。保持袖肥不變增加袖山高，袖山弧線隨之變長，縫縮量隨之增大，這時所呈現(xiàn)的裝袖角度較小，反之亦然[10]。

2 實驗部分

以袖山高、縫縮量及裝袖角度為變量，選用相同的面料，以原型為基礎(chǔ)，保證袖窿相同，袖肥值固定為33 cm，袖山高從13.75 cm開始以0.5 cm為檔差增加長度，縫縮量相應(yīng)發(fā)生變化，縫制出7個袖山高不同的小樣，測量并記錄相應(yīng)縫縮量和裝袖角度,形成7組數(shù)據(jù)，袖子結(jié)構(gòu)如圖1所示，袖山高為13.75 cm的樣衣如圖2所示。

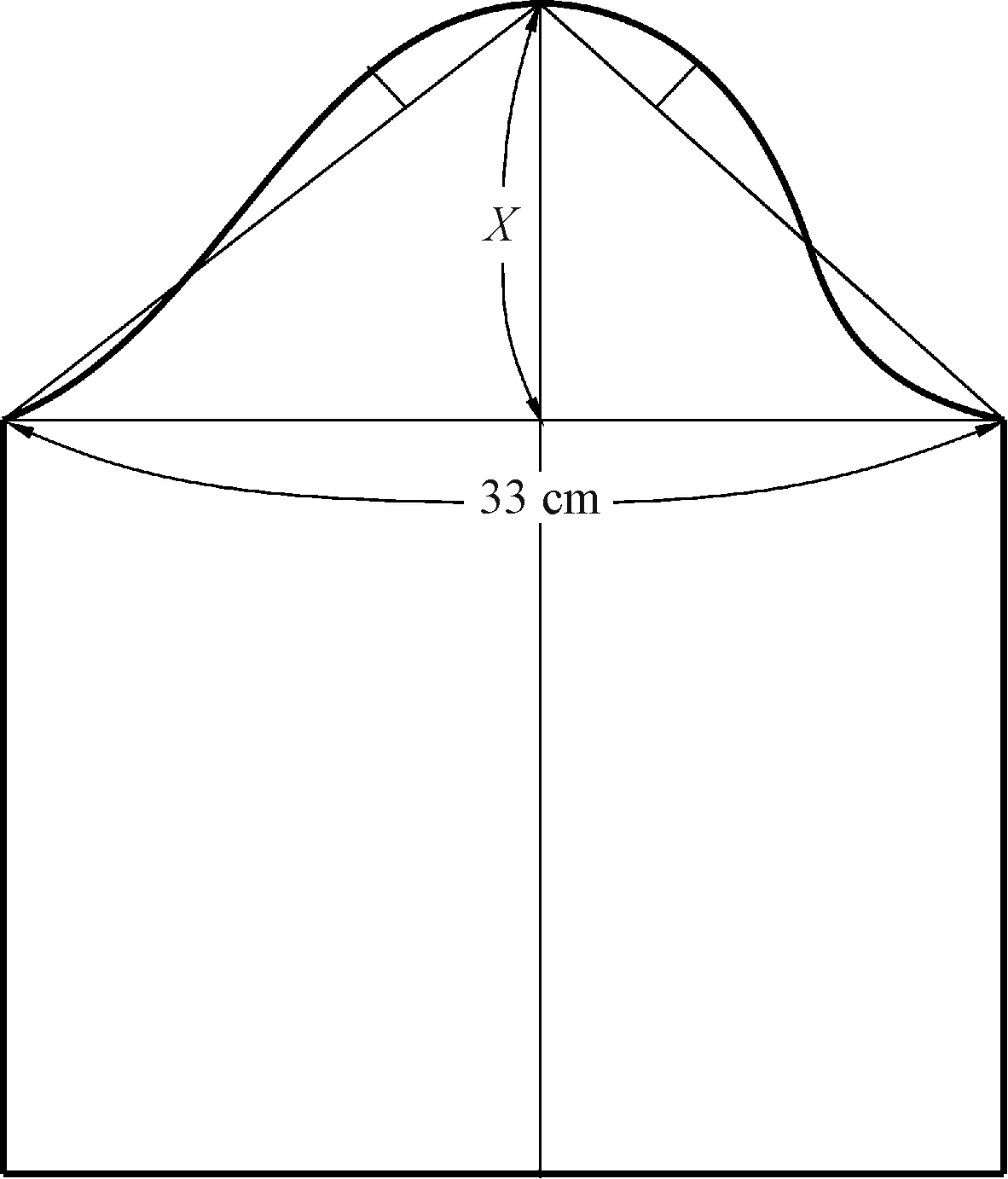
圖1 袖子結(jié)構(gòu)

圖2 袖山高為13.75 cm的樣衣

3 實驗結(jié)果與分析

3.1 縫縮量和袖山高的定量研究

根據(jù)實驗?zāi)康模涗浢拷M袖山高及對應(yīng)的縫縮量，通過MATLAB軟件將7組實驗數(shù)據(jù)進行擬合，可以發(fā)現(xiàn)，在袖窿、袖肥一定的情況下，縫縮量和袖山高呈現(xiàn)正相關(guān)線性關(guān)系，這與經(jīng)驗是一致的，袖山高越大，縫縮量越大。袖山高與縫縮量的線性關(guān)系如圖3所示。

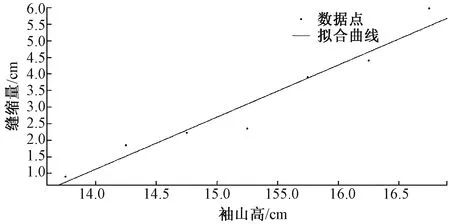
圖3 袖山高與縫縮量的線性關(guān)系

根據(jù)圖3的線性圖像，得出控制變量條件下的關(guān)系式：

y=1.572x-20.89

(1)

式中：y為縫縮量，cm；x為袖山高,cm。

實驗擬合出的數(shù)據(jù)圖像為線性圖像，在袖山高為13.75 cm至16.75 cm逐漸遞增時，縫縮量與袖山高大致呈現(xiàn)正相關(guān)的一次線性關(guān)系。即在控制其他條件不變的情況下，可以通過這2個量的任意一個量得出另一個量的近似值，當(dāng)其他條件改變時，也可以改變系數(shù)和常量來得出新的關(guān)系式，直觀地展現(xiàn)出這2個變量的相關(guān)關(guān)系，在平面制圖及計算機輔助設(shè)計中可以更加方便地得出相應(yīng)數(shù)據(jù)。

3.2 裝袖角度和袖山高的定量研究

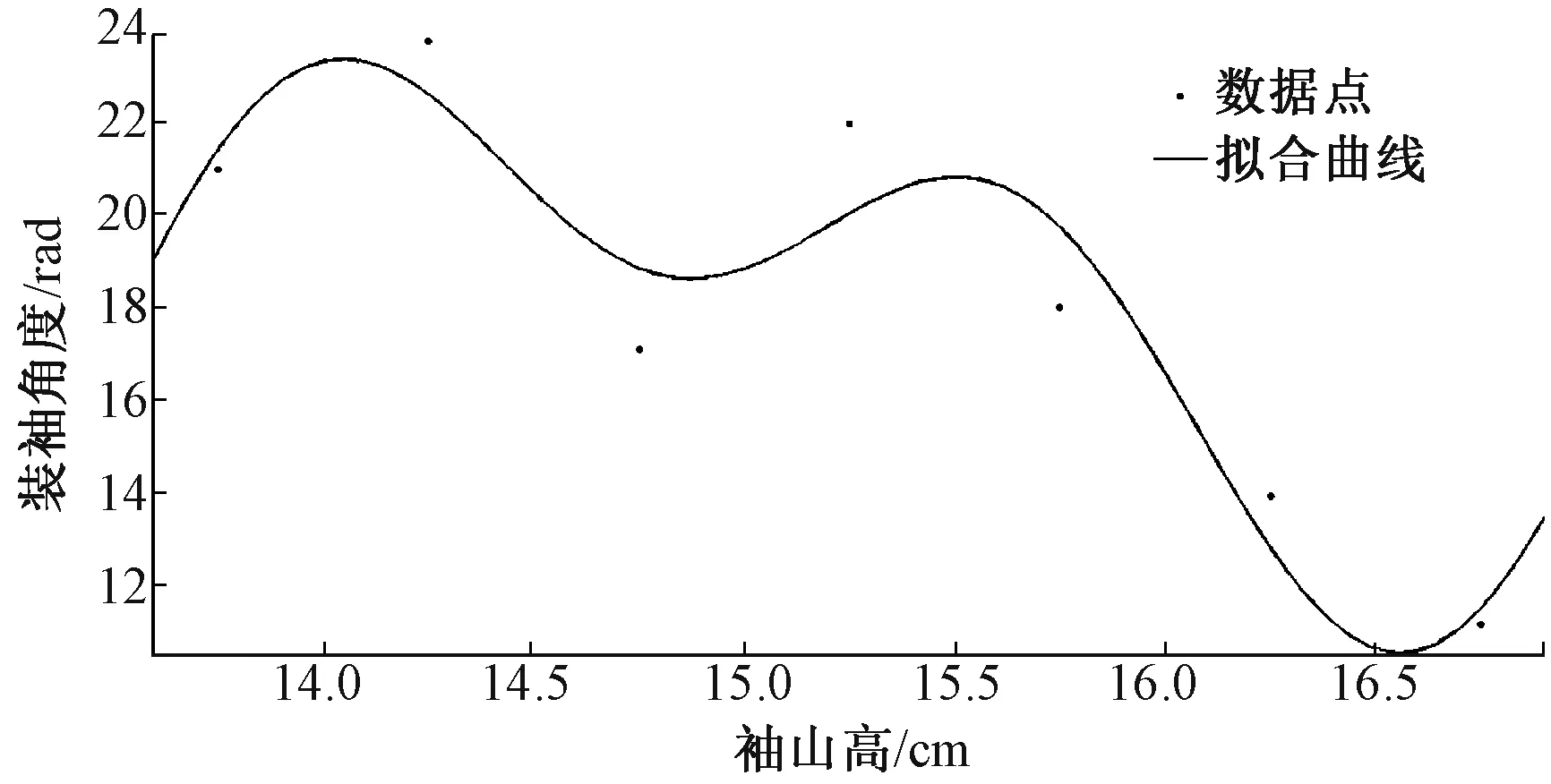
圖4 袖山高與裝袖角度的擬合圖像

根據(jù)實驗?zāi)康模涗浢總€袖山高對應(yīng)的裝袖角度。在控制其他條件不變的情況下，裝袖角度隨袖山高變化而呈現(xiàn)不穩(wěn)定的變化，直接用經(jīng)驗無法分析相關(guān)關(guān)系，因此需要定量研究數(shù)據(jù)之間的相關(guān)關(guān)系。通過MATLAB軟件將所得數(shù)據(jù)進行擬合，袖山高與裝袖角度的擬合圖像如圖4所示。

根據(jù)圖4的線性圖像擬合，得出控制變量條件下基于二次傅里葉擬合的函數(shù)關(guān)系式：

(2)

式中：f(x)為裝袖角度，rad，x為袖山高,cm；

a0=0.315 30(0.006 167,0.624 5)

a1=0.072 35(-1.111,1.256)

b1=0.020 33(-3.659,3.699)

a2=-0.022 77(-5.605,5.559)

b2=-0.055 44(-2.667,2.556)

w=1.739(-1.591,5.069)

由實驗數(shù)據(jù)和圖像不難看出，袖山高長度在較低范圍內(nèi)，裝袖角度隨袖山高的增加而升高，并在剛剛超過14 cm處達到峰值，隨之較為平緩地下降，在接近15 cm的位置到達谷值。在袖山高繼續(xù)上升的過程中，裝袖角度在15.5 cm的位置上達到第2個峰值隨之較為快速地下降，在超過16.5 cm的位置上達到第2個谷值。擬合圖像體現(xiàn)在裝袖外觀上為裝袖角度先隨著袖山高的增加而緩慢增加，隨著縫縮量到達一定的閾值，由于袖山縮縫導(dǎo)致袖山處向內(nèi)擠壓，裝袖角度隨之減小，在此過程中裝袖角度出現(xiàn)一定的反復(fù)，但峰值小于第1個峰值，總體趨勢是裝袖角度隨袖山高的增大而減小，在袖山高超過16.5 cm后基本很難實現(xiàn)圓順美觀的效果因此不予考慮。

4 結(jié)束語

在符合上述條件和數(shù)值范圍的情況下，應(yīng)用本文式(1)(2)可計算出袖窿、袖肥一定時，不同袖山高對應(yīng)的袖山縫縮量和裝袖角度，當(dāng)袖窿或袖肥變化時，只需將相應(yīng)系數(shù)和常數(shù)變化得出新的關(guān)系式。在紙樣上，當(dāng)袖山縫縮需要達到一個具體的量時，可根據(jù)式(1)調(diào)整袖山高使之達到期望效果；同理，為了滿足服裝設(shè)計和不同著裝條件下對裝袖角度的不同需求，可應(yīng)用式(2)在13.75～16.75 cm范圍內(nèi)通過調(diào)整袖山高的長度來控制裝袖角度的大小。在實際應(yīng)用時，不僅要考慮到設(shè)計要求，還要考慮人體穿著的舒適性，同時還需要考慮到不同面料對這些變量間關(guān)系的影響。因此，文中式(1)(2)存在一定的局限性，缺乏更為廣泛的數(shù)據(jù)分析和與其他變量間的關(guān)系分析；同時，實驗過程和實驗方法還需要通過進一步的優(yōu)化得出更加接近真實變量關(guān)系的關(guān)系式，以期更好地為設(shè)計美觀合體的袖型而服務(wù)。