基于納米流體的PMSM熱平衡分析
井志華,楊 綠,徐 達,樊艷娥,何 鋒,吳懷超,袁 焱
(1.貴州大學,貴州 550025; 2.貴陽航空電機有限公司,貴州 550025)
0 引 言
永磁同步電機(以下簡稱PMSM)具有功率因數高、起動力矩大、功率密度高等特點,被廣泛應用于電動汽車、軌道交通、船舶推進、航空航天和國防等諸多領域[1]。中高功率PMSM的熱損耗較大,溫升過高會引起永磁體退磁、輸出轉矩下降、絕緣氧化、潤滑失效等問題,因此其散熱系統設計是PMSM設計中的關鍵問題之一。
常見的電機散熱措施主要有自然散熱、強迫風冷和液冷三種形式[2]。已有文獻研究表明,三種散熱措施的散熱能力大小依次為液冷、強迫風冷和自然冷卻,針對中高功率PMSM采用液冷散熱方式可較易滿足所需的熱平衡溫度[3-4]。同時,一些研究通過優化流道和流速,還可進一步降低電機的工作溫度和體積。如文獻[5]基于MATLAB和CFD數值計算軟件找出了適合水道結構截面尺寸;文獻[6]采用有限體積法研究了電機內、外流體流動性能,得到了電機內部空氣流動的分布規律。近年來,隨著納米技術的發展,納米流體作為散熱介質受到了國內外研究者的關注。文獻[7]通過采用氧化石墨烯納米流體來提高汽車散熱器的性能,結果表明,與基液相比,納米流體能夠較好地提高汽車散熱器的性能。隨著新能源汽車的快速發展,電動汽車用PMSM的輕量化與熱管理系統設計需要進一步壓縮散熱結構尺寸和優化散熱工藝參數,因此,基于新型納米流體散熱介質,探討其對電動汽車用PMSM的散熱效果與結構優化,具有突出的現實意義。
本文以一臺45 kW表貼式PMSM為例,采用有限體積法對電機溫度場進行計算分析。通過分析改變傳熱介質、流體流量和流道大小對電機溫度場的影響,揭示了納米流體作為傳熱介質相較于傳統傳熱介質能夠顯著降低熱平衡溫度,得出了流體流量和流道大小對電機溫度場的影響規律。
1 PMSM結構及損耗
本文以一臺45 kW表貼式PMSM為研究對象,采用液冷方式對電機進行冷卻。電機結構的簡化模型如圖1所示,流體流道為螺旋結構如圖2所示,基本參數如表1所示。

圖1 電機模型
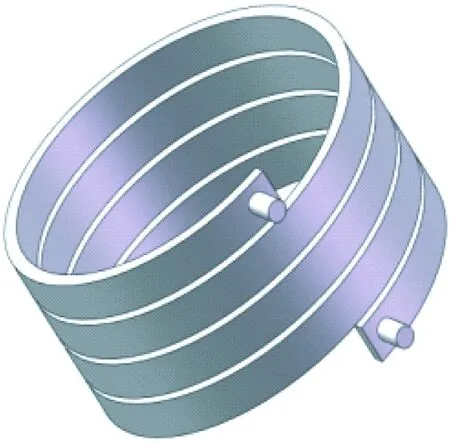
圖2 流體流道

參數數值額定功率P/kW45額定電壓u/V480額定轉速n/(r·min-1)3 500
電機損耗主要包含定子鐵耗、繞組銅耗、轉子損耗和摩擦損耗。本文電機損耗參考文獻[8]進行計算。
2 PMSM穩態溫度場數學模型
根據傳熱學基本原理可知,電機溫度場處于穩態時,導熱不隨時間項變化,其三維穩態含有熱源、各向異性材料的熱傳導方程,在直角坐標系下可表示[9-10]:
(1)
式中:T為PMSM待求溫度;kx,ky,kz分別為材料在x,y,z方向的導熱系數;Q為求解域內各熱源體密度之和;n為單位法向矢量;α為散熱面的散熱系數;Tf為散熱面周圍流體溫度。
3 PMSM溫度場求解域的確定
3.1 基本假設
為了建立PMSM三維溫度場求解域,合理簡化求解過程,對電機做如下基本假設[10-12]:
1) 忽略溫度變化對導熱系數和散熱系數的影響;
2) 定子槽內浸漬狀態良好,浸漬漆填充均勻,且銅線絕緣漆分布均勻;
3) 槽絕緣和鐵心緊密結合在一起;
4) 電機液冷時,由于流體流速遠小于聲速,馬赫數很小,因此將流體作為不可壓縮流體處理;
5) 流體在電機流道內流動時,其雷諾數很大,故采用湍流模型對電機內的流場進行求解;
6) 忽略重力、磁場對冷卻介質的影響;
7) 各個固體部件之間接觸良好,忽略接觸熱阻。
3.2 模型等效
為了便于對PMSM的溫度場進行仿真分析,結合電機結構、傳熱和冷卻系統的特點,對電機做如下等效:
1) 定轉子間氣隙等效
電機轉子旋轉時,帶動周邊空氣運動,相應提高了對應位置的散熱能力。因電機內部氣體流動的無序性,其對流散熱系數難以確定。為了簡化計算,將流動的空氣等效為有效導熱系數為λe的靜止空氣,此時,定轉子之間流動氣體的換熱能力的等效方法如下[13-14]:
(2)
式中:Re為氣體雷諾數;μ為轉子表面的線速度;δ為氣隙長度;λ為空氣的運動粘度。
氣體中臨界雷諾數:
(3)
當Re>Reer時,氣體流動為紊流狀態,其有效導熱系數λe可表示:
λe=0.001 9η-2.908 4Re0.464 1ln (3.333 61η)
(4)
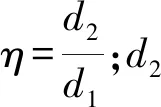
2) 繞組絕緣的等效
定子繞組是由直徑較小銅線繞制而成,表面涂有絕緣層,其在定子槽內排列不均勻、無規律,沒有完全填充整個槽,因此繞組槽內實際模型較為復雜。為使計算簡便,假設:定子槽內的導線排列均勻,沒有溫差;銅線表面的絕緣漆均勻分布;浸漬漆完全填充繞組槽。根據假設,將槽內所有導線看作一個導熱體,對稱分布在槽中間;將導線外部的絕緣漆、環氧、絕緣紙以及少量的空氣等效為一個材料均勻導熱體,分布在導線的周圍,其等效模型如圖3所示。
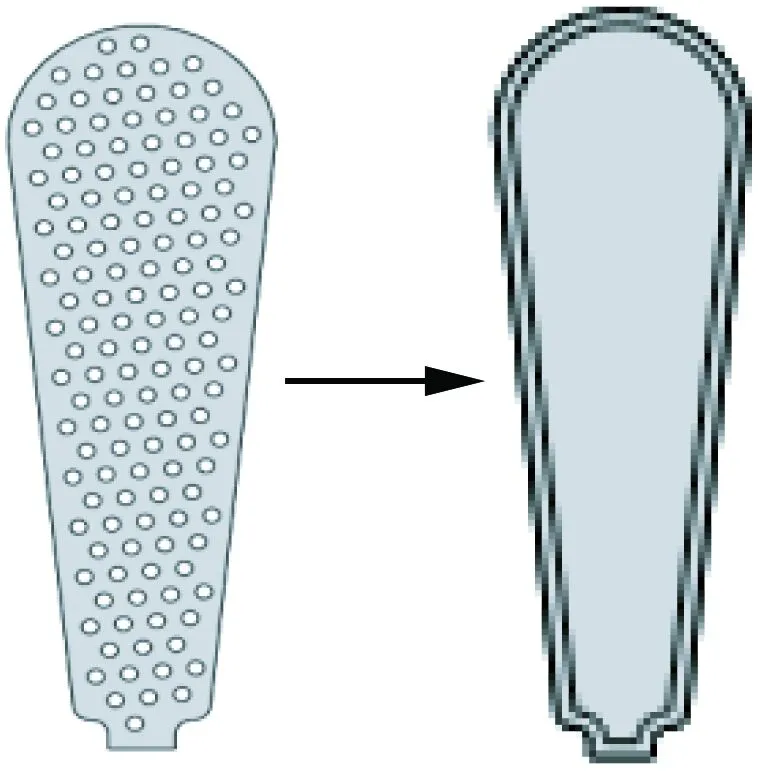
圖3 繞組等效模型
等效槽內絕緣層的導熱系數參考文獻[15]進行計算:
(5)
式中:δi為每個導熱體的厚度;λi為每個導熱體的導熱系數。在本文中,λeq=0.09 W/(m ·℃)。
3) 定轉子導熱系數的等效
工程上定轉子鐵心是由很多個沖片疊壓而成,沖片與沖片之間涂有絕緣漆,造成定轉子鐵心軸向導熱系數與徑向和周向導熱系數不同。在求解過程中,要把電機定轉子鐵心分別等效為一整個實體。此時,根據傳熱學理論,將鐵心沖片軸向傳熱看作多沖片平壁串聯導熱,將鐵心周向和徑向傳熱看作硅鋼片多層平壁并聯導熱。其導熱系數計算如下[16]:
(6)
(7)
式中:λz,λr和λθ分別為軸向、徑向和周向導熱系數;δFe為定子鐵心硅鋼片的凈長;δ0為絕緣介質的凈長;λ1為定子鐵心中硅鋼片的導熱系數;λ0為鐵心疊片絕緣介質的導熱系數;KFe為定子鐵心的疊裝系數。
3.3 散熱系數的確定
電機散熱系數受電機工藝、使用材料、材料導熱系數等因素影響,以致較難得到準確的計算模型。通常電機散熱系數是借助經驗公式來進行計算,其計算公式如下[15-16]:
定子鐵心端面散熱系數:
(8)
式中:v為轉子表面的旋轉線速度。
轉子端面散熱系數:
(9)
機殼散熱系數:
外殼向周圍介質散熱的自然散熱系數根據經驗公式計算:
(10)
式中:v為機座內壁的風速,若為自然冷卻,v=0;T0為機座外壁的空氣溫度。本文中,定子鐵心端面散熱系數α1=22.2 W/(m2·K),轉子端面散熱系數α2=28 W/(m2·K),機殼散熱系數α3=14 W/(m2·K)。
4 模型求解及結果分析
為了獲取不同傳熱介質、散熱管道當量直徑以及不同介質流體流量對PMSM全域溫度的影響及其規律,運用Fluent求解圖1的PMSM和圖2的散熱水道溫度場模型。分別求解水(W)、銅納米流體(NF-Cu)和石墨烯納米流體(NF-G)三種傳熱介質在不同當量直徑以及不同介質流體流量情況下的溫度場。傳熱介質基本參數如表2所示。

表2 流體編號與基本參數[17-18]
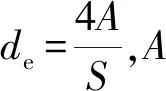

圖4 電機網格模型
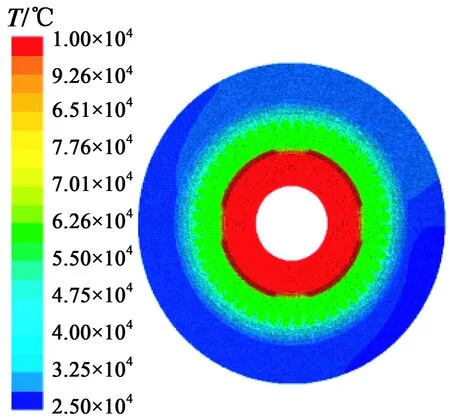
圖5 電機溫度場仿真模型
4.1 流體流量對電機溫度場的影響
通過Fluent軟件,基于有限體積法對電機溫度場進行仿真,其流道截面當量直徑為15 mm。傳熱介質分別為水、銅納米流體和石墨烯納米流體,通過改變電機入口流量,分別求解得到電機熱平衡溫度,結果如圖6所示。
從圖6可以看出,在滿足某一電機全域溫度條件時,石墨烯納米流體、銅納米流體和水的流量依次增加。其中,在97.8 ℃時,對應的石墨烯流體流量為10 L/min,水的流量約為14.5 L/min。相對于傳統水介質,石墨烯流體流量下降約30%,從而大幅節省散熱泵功率。
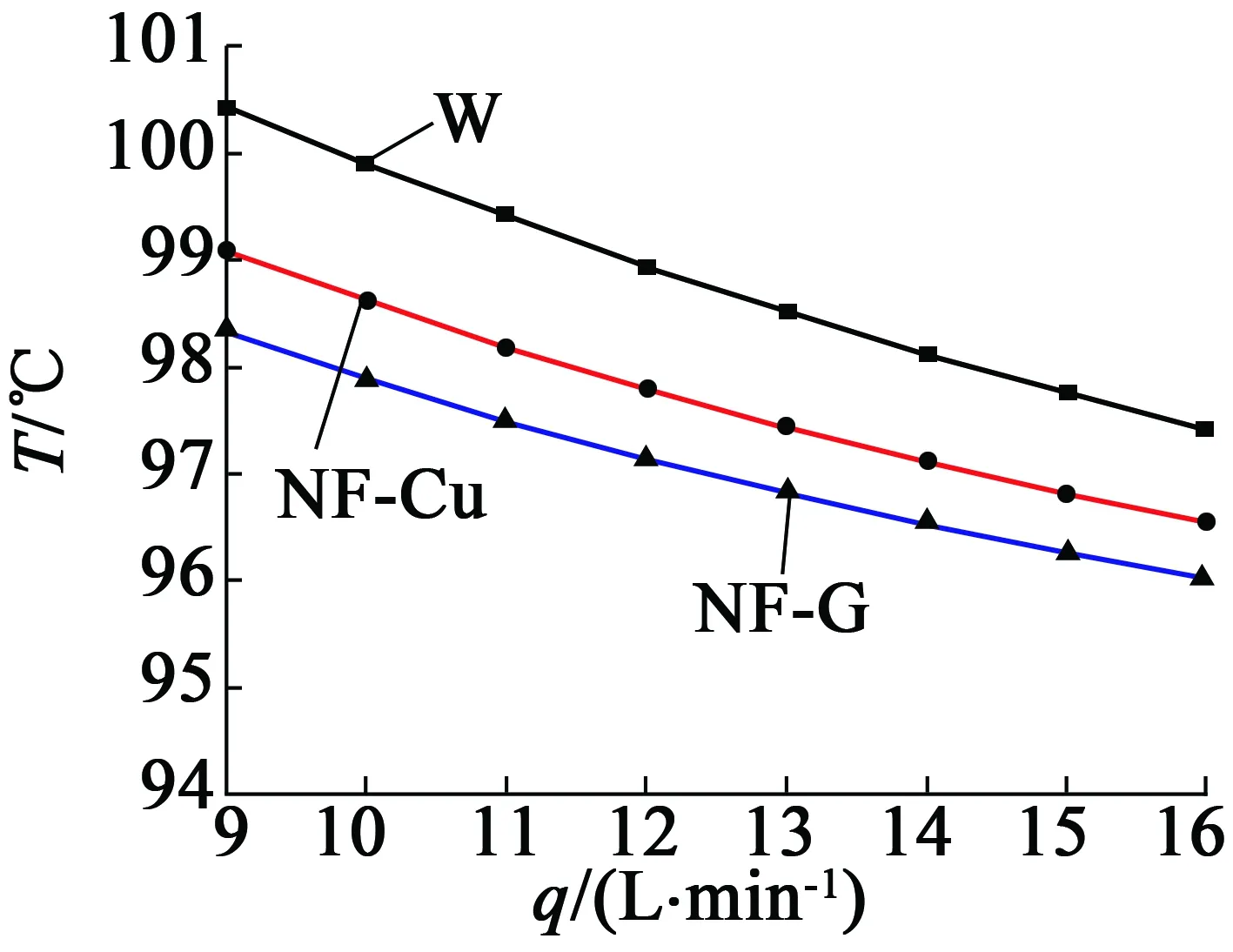
圖6 電機全域溫度隨流量變化圖
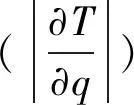
為了進一步量化傳熱介質流量對電機全域溫度的影響規律,應用回歸分析方法,得出了水、銅納米流體和石墨烯納米流體與電機全域溫度之間關系的回歸模型:
(11)
式中:T為電機全域溫度值;q為流體流量。
4.2 流道當量直徑對PMSM熱平衡溫度的影響
維持散熱介質流量不變,求解不同周向矩形截面螺旋流道當量直徑時電機熱平衡溫度,得出流道當量直徑對PMSM熱平衡溫度的影響。求解中不同流道相關參數如表3所示。
邊界定義流體入口流量為10 L/min,電機熱平衡溫度隨流道當量直徑和流速的變化曲線如圖7所示。
從圖7可以看出,維持流量不變,在所考察的當量直徑區間內,de約為16 mm時所對應的電機熱平衡溫度取較低值。電機熱平衡溫度總體上隨當量直徑的增大呈增大趨勢。這是因為,當電機散熱介質流體流量為一定值時,流體流速v隨流道當量直徑de的增大而減小,流速降低造成流體與流道之間的對流散熱系數下降,而流速對散熱效率的影響大于當量直徑所致。
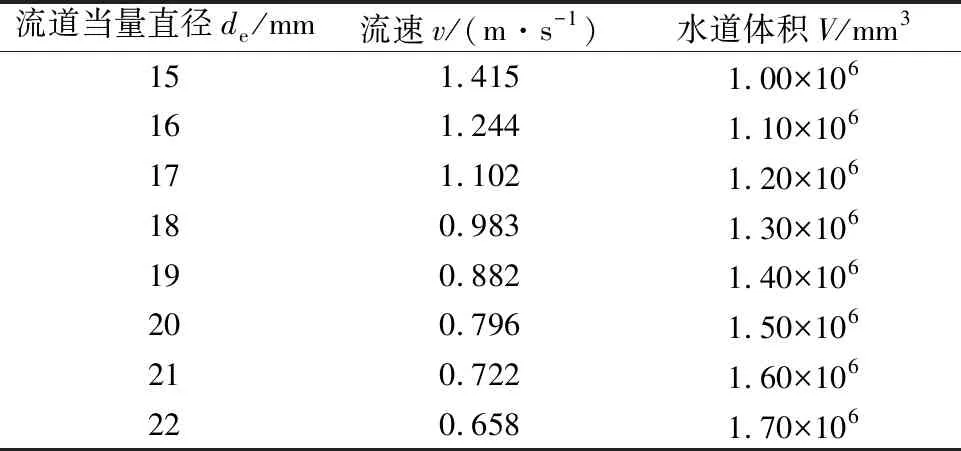
表3 流道基本參數
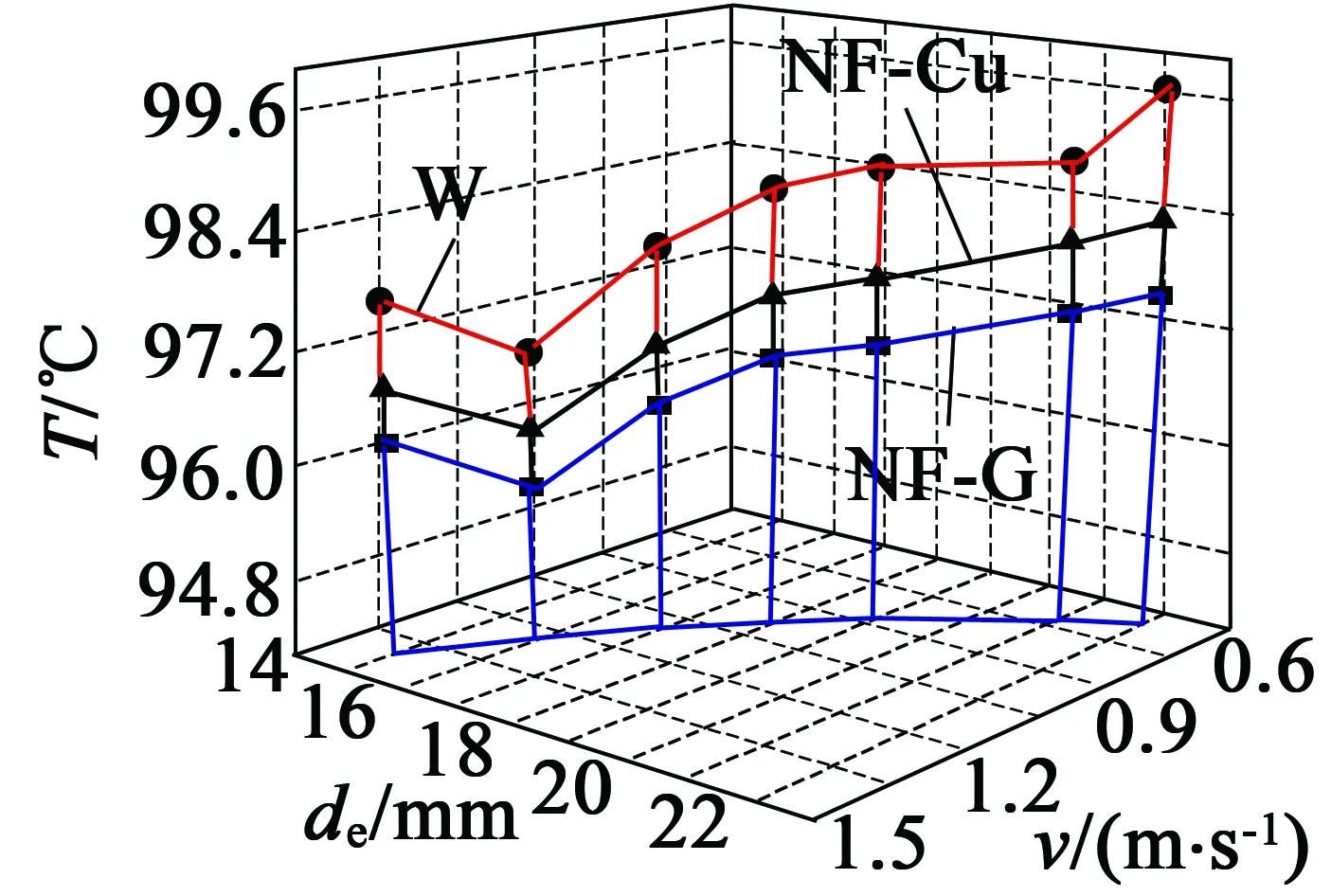
圖7 電機熱平衡溫度與流道當量直徑之間的關系曲線
5 結 語
本文以一臺45 kW表貼式PMSM為例,應用有限體積法分別求解熱平衡方程,揭示了不同傳熱介質、散熱管道當量直徑以及不同介質流體流量對PMSM全域溫度的影響及其規律。主要結論如下:
1) 熱平衡溫度一定時,石墨烯納米流體、銅納米流體和水的流量依次增加。其中,在97.8 ℃時,相對于傳統水介質,石墨烯納米流體流量下降約30%,從而可較大幅度節省散熱泵功率。
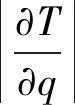
3) 流量一定時,在本文考察的當量直徑區間,流速對散熱效率的影響大于當量直徑,且PMSM熱平衡溫度總體隨著當量直徑的增大呈增大趨勢。

