基于VSIMM-CKF的機場場面運動目標跟蹤*

孫壽宇 宮淑麗

(南京航空航天大學民航學院 南京 210016)

0 引 言

機場場面管理需要對場面活動區進行有效的交通管理，國際民航組織于2004年提出在機場部署“先進場面運動引導控制系統”(advanced surface movement guidance and control system, A-SMGCS)的概念[1]，A-SMGCS概念提出基于保障機場安全和增大機場容量兩大因素，實現監視、路徑選擇、引導和控制功能[2]，其中監視功能是整個系統功能的基礎[3].目前我國大型國際樞紐機場均安裝有場面監視雷達(surface movement radar, SMR)，配合目視監視、語音通信等實現對機場場面活動區域的運動目標的監視與引導[4].由于SMR測量數據含有噪聲，需要對SMR得到的航跡數據進行濾波處理.常用的非線性估計方法是基于傳統的Taylor級數展開的擴展卡爾曼濾波(extended kalman filter, EKF)算法.EKF思想是將非線性系統一階線性化，但是線性化過程會帶來近似誤差.Julier[5]提出的無跡Kalman濾波(unscented Kalman filter, UKF)以無跡變換(unscented transformation, UT)為基礎,摒棄了對非線性函數線性化的傳統做法，因而計算精度較高.UKF雖然不需要計算Jacobin矩陣，但只有選擇合適的參數才能保證其收斂性.Arasaratnam等[6]提出的容積卡爾曼濾波(cubature Kalman filter，CKF)基于球面徑向積分準則，利用2n個具有相同權重的容積點對狀態的概率密度分布函數進行逼近，避免復雜的雅克比矩陣的運算，提高了濾波的精度和穩定性.許多學者基于CKF做了大量研究，如文獻[7]，針對容積卡爾曼濾波器在遞推過程中，計算量大、數值不穩定等問題，提出平方根容積卡爾曼濾波.文獻[8]將牛頓高斯迭代法引入了平方根容積卡爾曼濾波提出改進迭代平方根容積卡爾曼濾波，文獻[9]基于采樣點正交變換改進CKF提出了TCKF.

交互式多模算法(interacting multiple model, IMM)通過馬爾可夫鏈可實現各個模型之間的軟切換，增加了模型之間的交互功能.文獻[10]將IMM算法和CKF相結合對彈道再入目標跟蹤研究，文獻[11]將IMM算法和EKF相結合對中段彈頭跟蹤研究，文獻[12]將IMM算法和UKF相結合對機場場面目標跟蹤研究.IMM是一種固定結構的多模型算法，Li[13]創立了使用時變模型集的變結構交互式多模型算法(variable structure interacting multiple model, VS-IMM).該算法可以優化模型集，減少系統的計算量，提高跟蹤的精度.文獻[14]采用自適應網格對模型集進行調整，結合基于S修正RBUKF濾波算法，文獻[15]提出基于球面徑向容積規則的平滑變結構濾波算法.本文將VSIMM算法與CKF相結合，采用VSIMM-CKF算法，應用于機場場面監視.

1 場面運動目標運動模型建立

1.1 上海虹橋機場地形信息

上海虹橋國際機場采用雙跑道、雙航站樓運行管理的模式.滑行道系統為進、出港飛機提供跑道和機坪之間的聯系通道，滑行道系統關系著機場的運行效率和運行安全水平[16]，見圖1.為了能夠統一時間實現多架飛機的穿越需求，提高飛機運行效率，飛行的跑道穿越滑行是不可避免的，保障飛機安全穿越跑道滑行對此進行場面監視至關重要.

圖1 虹橋機場北流向機場地形信息圖

1.2 飛機運動模型

飛機的運動包含三種運動：在跑道上加速運動，在跑道與滑行道或滑行道與滑行道連接處的勻速轉彎運動，在滑行道上勻速直線運動.

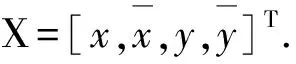
X(k)=FCV(k-1)X(k-1)+GCV(k-1)W(k-1)

(1)

式中：FCV為CV模型的運動轉移矩陣.

(2)

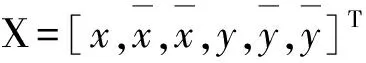
X(k)=FCA(k-1)X(k-1)+

GCA(k-1)W(k-1)

(3)

式中：FCA為CA模型的運動轉移矩陣.

(4)

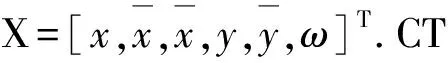
X(k)=FCT(k-1)X(k-1)+

GCT(k-1)W(k-1)

(5)

式中：FCT為CT的運動轉移矩陣.

(6)

2 容積卡爾曼濾波

為了解決求解多變量非線性函數與高斯密度函數乘積的積分，Arasaratnam提出容積卡爾曼濾波，即通過三階容積積分法則，利用2n個容積點加權求和近似計算加權高斯積分，對于函數f(x)的加權高斯積分：

(7)

式中：N(x;μ,P)為x服從均值μ和協方差陣P的正態分布；S滿足S·(S)T=P，具有2n個元素的容積點集{ξi}具有如下形式.

CKF算法流程見圖2.

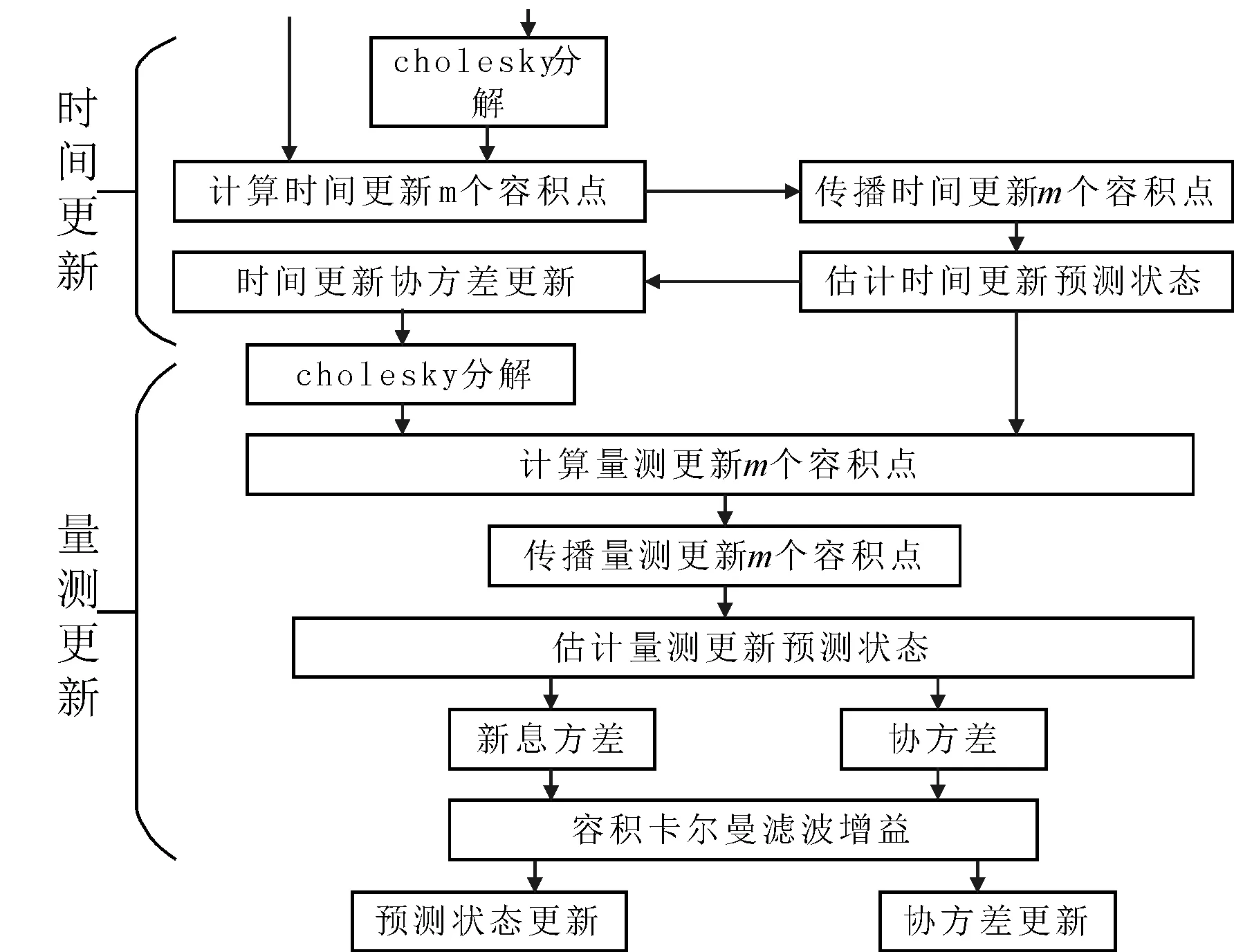
圖2 CKF算法流程圖

具體流程如下：

1) 時間更新

①假設在第k時刻后驗密度函數

p(Xk-1|Dk-1)=N(xk-1|k-1,Pk-1|k-1)已知，Pk-1|k-1可以分解為

(8)

②計算容積點(i=1,2,…,m)

Xi,k-1|k-1=Sk-1|k-1ξi+xk-1|k-1

(9)

這里m=2n.

③傳播容積點(i=1,2,…,m)

(10)

④估計預測狀態

(11)

⑤協方差更新

(12)

2) 量測更新

①Pk|k-1分解

(13)

②計算容積點

Xi,k|k-1=Sk|k-1ξi+xkξk-1

(14)

③傳播容積點

Zi,k|k-1=h(Xi,k|k-1,uk)

(15)

④計算量測預測值

(16)

⑤計算新息方差

(17)

⑥計算協方差矩陣

(18)

⑦計算容積卡爾曼濾波增益

(19)

⑧預測狀態更新

xk|k=xk|k-1+Wk(Zk-zk|k-1)

(20)

⑨協方差更新

(21)

3 基于VSIMM-CKF算法

運動目標的跟蹤研究主要取決兩個方面，首先，模型集的正確建立可以準確反應機動目標的運行狀態；其次，合適濾波算法可以有效濾除量測原因帶來的誤差.VSIMM算法模型集和概率轉移矩陣可根據目標的運動情況和地圖及其他因素等可變，在不同條件下使用不同的模型集，不僅能減少系統的計算量，而且能夠保證所選模型與系統運動相匹配，使MM估計器達到最優，提高跟蹤的精度.而對于非線性濾波問題，CKF算法比UKF算法更加嚴謹，可避免參數選取不當而造成濾波器性能下降.VSIMM-CKF算法利用VSIMM算法對模型集優化，同時在濾波方面采用更為嚴謹的CKF算法.

3.1 VSIMM算法

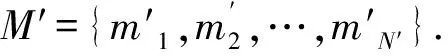
3.2 VSIMM-CKF算法

結合CKF的變結構多模算法流程見圖3.

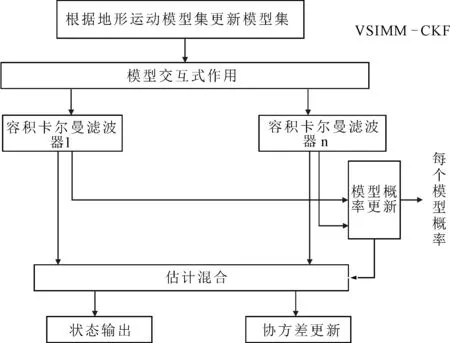
圖3 VSIMM-CKF算法流程圖

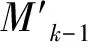
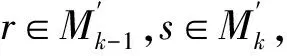
(22)

模型s的預測概率為

(23)

模型的混合概率為

(24)

(25)

(26)

3) CKF濾波見第2節

4) 模型概率更新 模型概率

(27)

(28)

5) 估計融合

(29)

(30)

4 仿真及結果分析

4.1 仿真場景設置

假設飛機在所在初始位置為(200 m，200 m),沿著跑道方向以初始速度為50 m/s，加速度為-2 m/s2直線運動20 s，然后以1 (°)/s的轉彎速率運動到B3，在40～60 s時沿著B3做勻速直線運動，然后以10 (°)/s的轉彎速度運動10 s運動至H3，最后在70～80s沿著H3做勻速直線運動.根據機場地形條件建立模型集，模型1為勻速直線運動；模型2為加速直線運動；模型3為轉彎率為1 (°)/s的左轉彎運動；模型4為轉彎率為5 (°)/s的右轉彎運動；模型5為轉彎率10 (°)/s的右轉彎運動.雷達采樣周期為1 s，考慮到SMR精度，距離方差19，方位角方差0.5.分別對IMM-EKF,VSIMM-UKF,VSIMM-CKF進行50次蒙特卡洛仿真實驗.

4.2 仿真結果分析

圖4為仿真過程中VSIMM-CKF每個模型的概率.

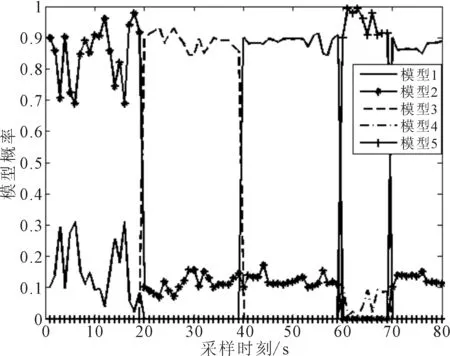
圖4 VSIMM-CKF每個模型算法概率

由圖4可知，VSIMM-CKF在每個時刻刪除了不必要的模型，從總模型集中選取了能反映目標真實運動狀態的2種運動模型進行了融合估計.

圖5為X,Y方向的位置RMSE曲線，圖6為X,Y方向的速度RMSE曲線.

由圖5可知，在初始時刻由于濾波器沒有跟蹤上，所以誤差X,Y位置誤差都較大.圖5a)中VSIMM-CKF在模型轉換時刻20 s左右、40 s左右等模型轉換時刻，即飛機做機動運動時誤差較大.而在非模型轉換時刻誤差基本維持在5 m以下，在模型轉換時刻峰值RMSE值大概16 m.IMM-EKF在模型轉換時刻峰值約為48 m,VSIMM-UKF在模型轉換時刻峰值約為28 m.圖6中一開始飛機沿著X軸平行運動不存在Y軸方向位移，所以誤差較低，在20 s左右飛機做機動運動時，誤差會增加.VSIMM-CKF峰值RMSE值為18 m，IMM-EKF峰值RMSE值為58 m，VSIMM-CKF峰值RMSE值約為28 m.由圖6可知，VSIMM-CKF誤差明顯要小于IMM-EKF和VSIMM-UKF.

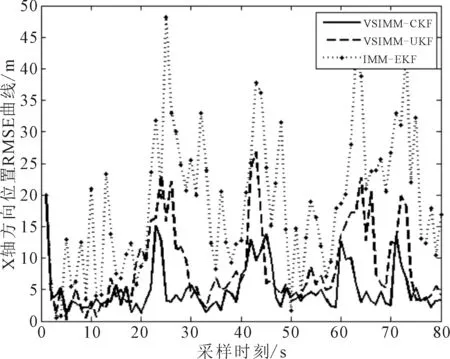
a) X方向

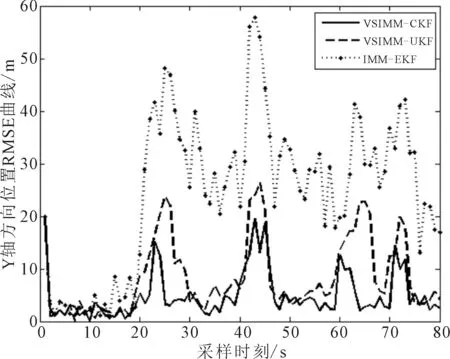
b)Y方向

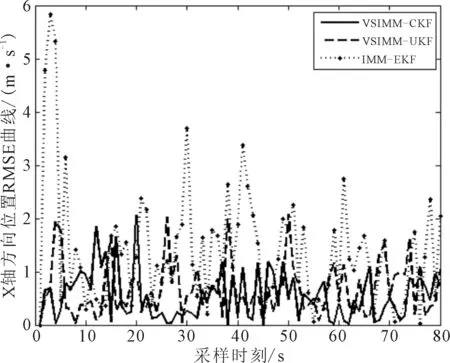
a) X方向

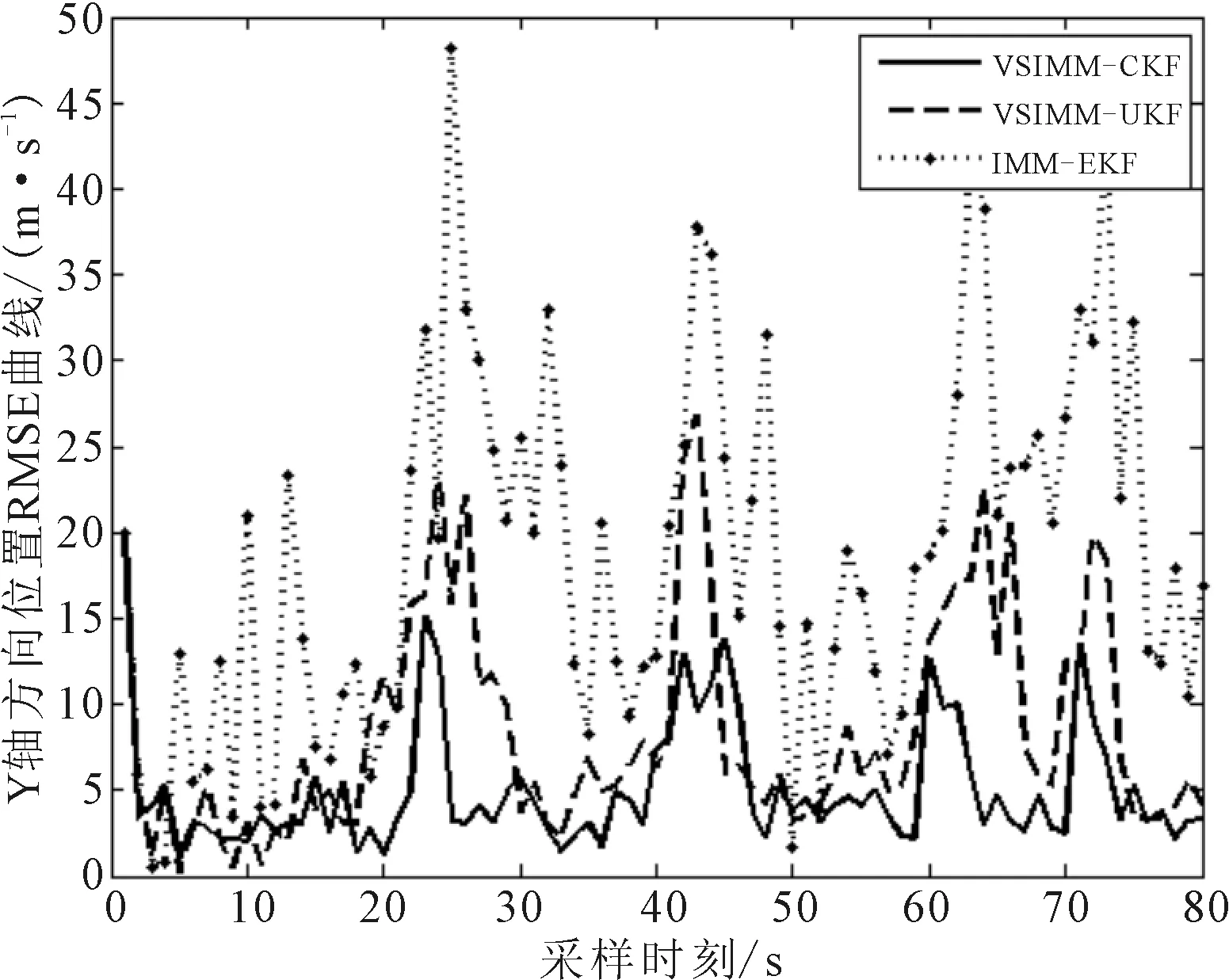
b)Y方向

表1為三種算法均方根誤差均值和運行時間.表中IMM誤差明顯高于VSIMM，主要是由于IMM算法中每個時刻需要計算所有模型的概率，對于模型較多時會增加計算的復雜度，導致精度下降.由于VSIMM-UKF需要進行頻繁的UT變換，也增加了計算的復雜度，而且，UKF可能會由于 點選取不當而導致精度下降.

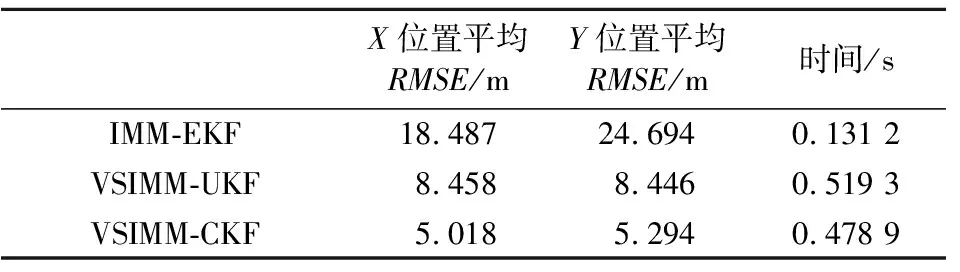
表1 三種算法均方根誤差均值和運行時間對比

5 結 束 語

針對機場場面上飛機的運動為例，結合上海虹橋機場地形信息，研究了基于SMR的機場場面單目標飛機運動監視.根據飛機的實際運動和機場地形信息，建立了五個運動模型.VSIMM算法使用時變的模型集，可避免IMM算法中模型之間不必要的競爭，減少計算量.CKF作為一種非線性濾波方法，以其對隨機變量非線性變換后概率分布具有良好的逼近精度的優勢得以發展.本文提出將CKF應用于VSIMM中，將VSIMM-CKF應用于機場場面飛機的監視中.并將VSIMM-CKF與IMM-UKF,VSIMM-UKF進行了仿真對比，仿真結果表明，VSIMM算法跟蹤精度明顯優于IMM算法，而且VSIMM-CKF計算時間要優于VSIMM-UKF,因此，將VSIMM-CKF應用于機場場面移動目標監視中能很好地完成單目標跟蹤，精確實時的單目標跟蹤算法也可以解決機場多目標跟蹤問題.