機匣螺栓連接分區域薄層單元建模方法

王 攀，臧朝平

（南京航空航天大學能源與動力學院，南京210016）

0 引言

螺栓連接結構憑借構造簡單、實用性強等優點，被廣泛應用于航空發動機機匣和轉子結構的連接。在工程應用中，螺栓連接件在承受工作載荷之前，需要對螺栓施加一定的預緊力，使螺栓和被連接件之間產生相互作用力，從而產生不同的接觸面連接剛度，進而影響結構的動力學響應。因此，螺栓連接結構建模方法的研究成為結構動力學研究領域的熱點問題[1]。螺栓連接的有限元模擬方法主要分為2類:非線性接觸算法和界面單元法。前者需要迭代計算結構響應，計算量較大。隨著有限元法的發展，Liu等[2-3]建立了螺栓連接部件的精細有限元模型，但由于其自由度數目龐大，不適用于復雜的連接結構；Ahmadian等[4-6]運用薄層單元法將連接結構接觸面等效為厚度很薄的實體單元，進行動力學建模，并運用優化算法修正薄層單元材料參數；馬雙超等[7]將薄層單元法運用到航空發動機領域；姚星宇等[8-9]給出薄層單元法在航空發動機機匣螺栓連接結構的建模原理，并研究了薄層單元材料參數對螺栓連接剛度的影響規律，但文獻中并未考慮由于施加不同的預載荷使螺栓法蘭連接結構實際接觸面積變化，以及接觸微凸體變形帶來的剛度改變影響整個裝配體的動力學響應。

本文基于螺栓連接結構的超模型連接剛度計算公式[10-12]，運用赫茲接觸理論以及M-B分形模型[13-16]，推導了不同預緊力螺栓連接簡化模型連接參數的計算公式，并以1個螺栓連接試驗機匣為例，對該簡化模型的仿真頻率與模態試驗測試頻率進行對比。

1 分區域薄層單元建模方法

1.1 分區域薄層單元

采用分區域薄層單元對螺栓連接部分進行簡化建模，如圖1所示。圖中綠色部分代表預緊力影響較弱的法蘭區域；紅色部分代表預緊力主要影響的螺栓區域。

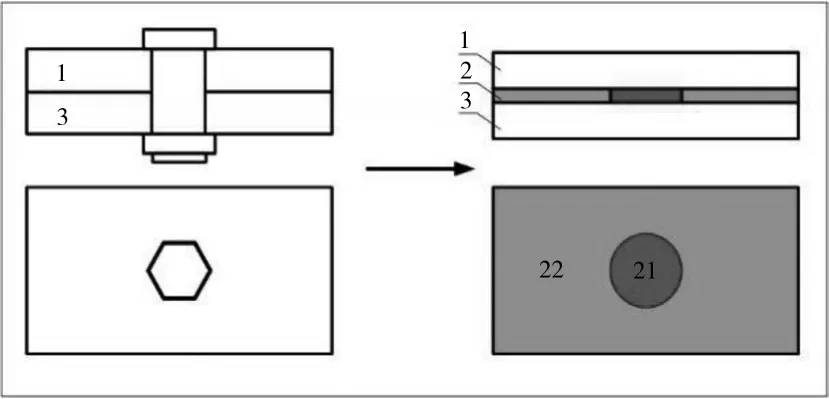
圖1 分區域薄層單元簡化模型

把上安裝法蘭1、薄層單元2和下安裝法蘭3視為串聯的彈簧結構，可得薄層單元連接結構的軸向總剛度

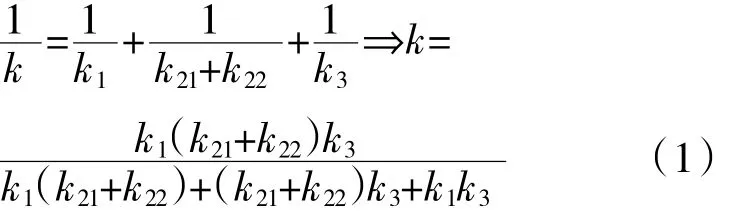
式中:k1、k21+k22和k3分別為上安裝法蘭、薄層單元和下安裝法蘭的軸向剛度；k21和k22分別為圖1中紅色部分薄層和綠色部分薄層的軸向剛度。

分區域薄層單元部分的軸向總剛度為

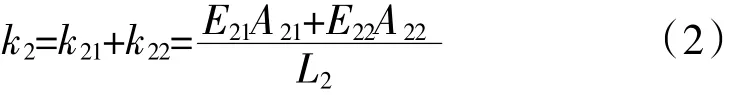
式中:E21和E22分別為圖中紅色區域和綠色區域的彈性模量；A21和A22分別為圖中紅色部分和綠色部分的面積；L2為薄層的厚度。

1.2 薄層單元軸向總剛度

對螺栓連接結構件進行靜力學分析，連接區域的應力分布集中在螺栓桿、螺母與被連接件接觸的區域，如圖2所示。其中螺栓連接結構的軸向連接剛度主要由螺桿連接的區域與預緊力作用的區域決定[8-9]。

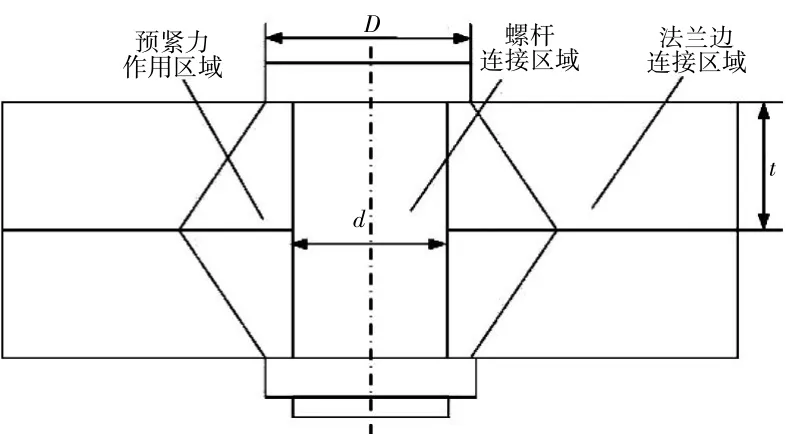
圖2 螺栓連接結構區域

螺桿連接區域的軸向剛度為

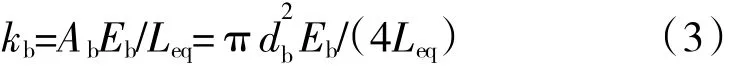
式中:Ab為螺栓桿的截面面積；db為螺栓桿的直徑；Eb為螺桿彈性模量；Leq為螺栓桿的當量長度。

對于螺栓預緊力作用區域，將被連接件的預緊力分布區域等效為切去頂端的錐形區域。可得該區域的連接剛度為

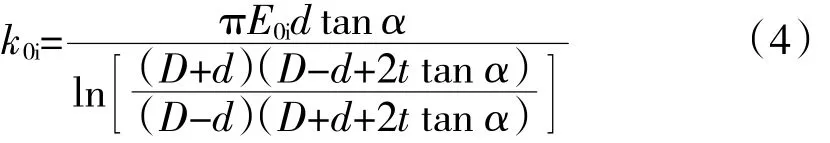
式中:E0i為被連接件的彈性模量；t為法蘭邊厚度；α為半錐形角，與螺栓預緊力F大小有關。

由于整個螺栓預緊力作用區域中，上下2個被連接件為串聯關系，則可知該區域的軸向連接剛度為

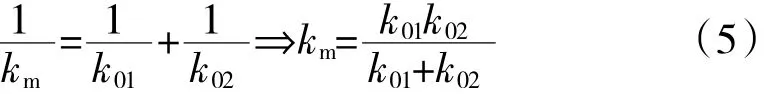
由此可得整個螺栓連接區域的連接總剛度ks

1.3 法蘭區域剛度

1.3.1 赫茲接觸理論

法蘭接觸面實質上由2個粗糙表面組成，粗糙表面的微凸體在外載荷作用下發生變形，如圖3所示。根據赫茲公式[13-14]可得微凸體法向載荷和彈性變形的關系

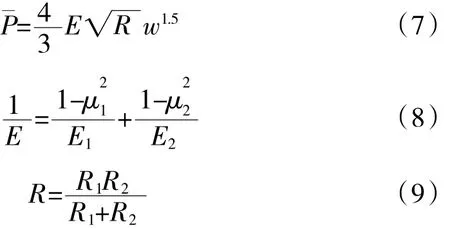
式中:E為2個接觸面的等效彈性模量；R為2個微凸體的等效接觸半徑；w為接觸點的法向變形量。微凸體接觸區域的接觸面積可以表示為a'=2πRw。

軸向載荷P對法向位移w求導，求解出微小接觸點的剛度為

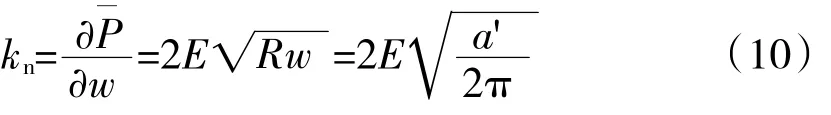
具有截面積的微凸體的變形[13-14]為

將式（11）帶入 a′=2πRw，可得微接觸點頂端的曲率半徑

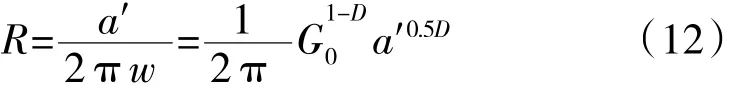
通過對大量試驗數據進行擬合[15]，可得金屬表面機械加工后的分形維數D、特征尺寸系數G與加工表面粗糙度Ra之間的關系式分別為

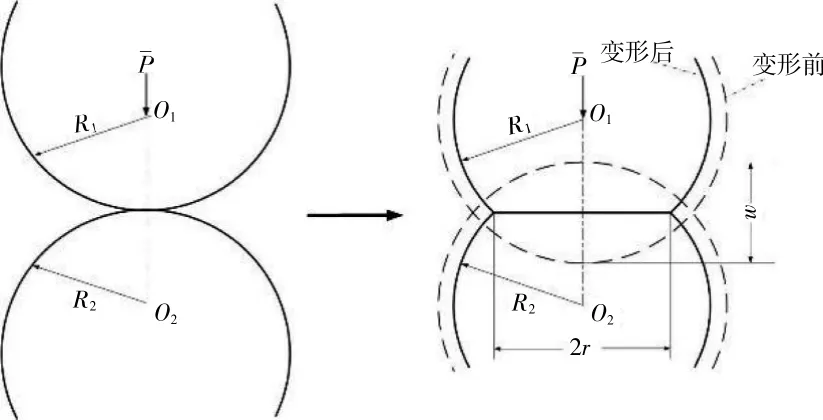
圖3 法向外載荷作用下的微凸體變形

1.3.2 M-B分形模型

粗糙表面中微凸體的近似分布形式如圖4所示。根據M-B分形模型[13-14]，微凸體截面積為a′的接觸點大小分布函數 n（a′）為

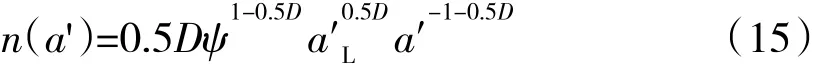
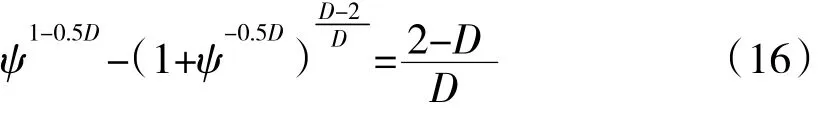
式中:ψ為加權系數

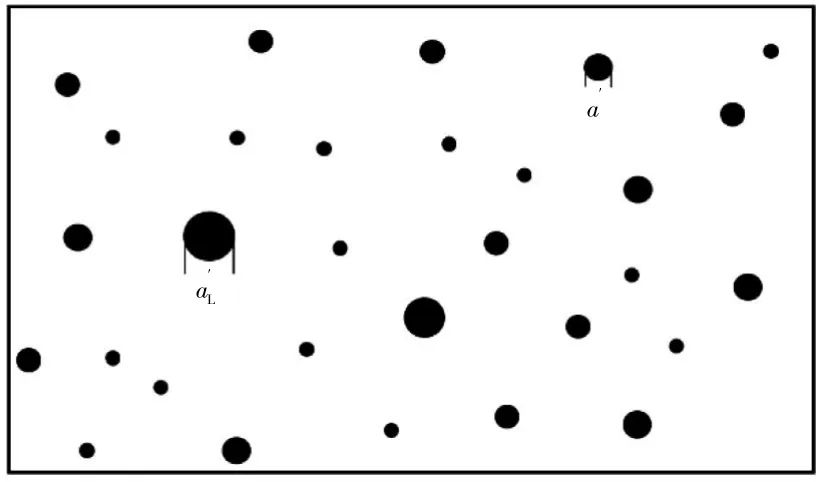
圖4 接觸表面微凸體分布

在接觸面處，區分彈塑性變形臨界面積a'c為

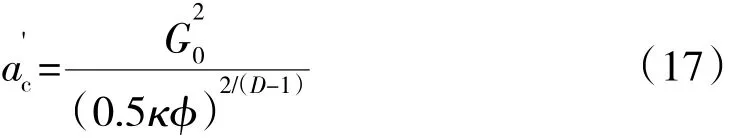
式中:κ=H/σs；Φ=σs/E；H 為較軟材料的硬度；σs為較軟材料的屈服強度。

微凸體的法向塑性形變載荷與接觸面積關系為

綜上所述，赫茲公式描述的單個微凸體的接觸剛度、M-B分形接觸模型以及結合面的法向接觸剛度，可由單個接觸點的剛度式（10）根據尺寸分布n（a'）積分得到

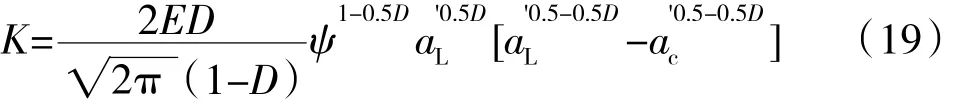
將式（11）（12）、帶入式（7），加上塑性形變載荷（18），根據尺寸分布積分，得到結合面的法向彈塑性總載荷

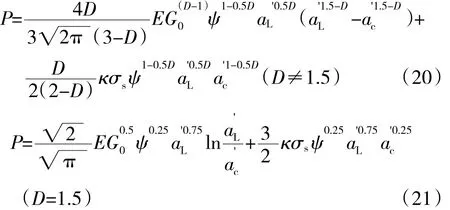
1.4 分區域薄層單元彈性模量

根據工程經驗，對于螺桿直徑為d的螺栓，擰緊力矩M和預緊力F之間相互換算的經驗公式為

法蘭的法向總載荷P即為所有螺栓的總預緊力，從而確定法蘭法向接觸剛度K作為分區域薄層單元中的法蘭區域剛度。再由螺栓連接部分的總剛度ks確定出螺栓區域剛度。之后，結合式（23）和式（24）可以求解出分區域薄層單元的彈性模量

2 螺栓連接機匣試驗

2.1 機匣靜力學分析

對于如圖5（a）所示的螺栓連接機匣，由36個M6螺栓連接。根據超模型的建模方法，采用實體螺栓結構建立機匣連接件的超模型。為了后續的靜力學分析，確定半錐形角。設定超模型網格尺寸為3 mm，采用2階4面體單元劃分網格，如圖5（b）所示。該連接模型共有148萬個節點，444萬個自由度。

圖5 連接機匣

在連接螺栓上分別施加 3、5、7、9、11 N·m 的預緊力，確定半錐形角，根據式（6）計算總剛度ks，見表1。

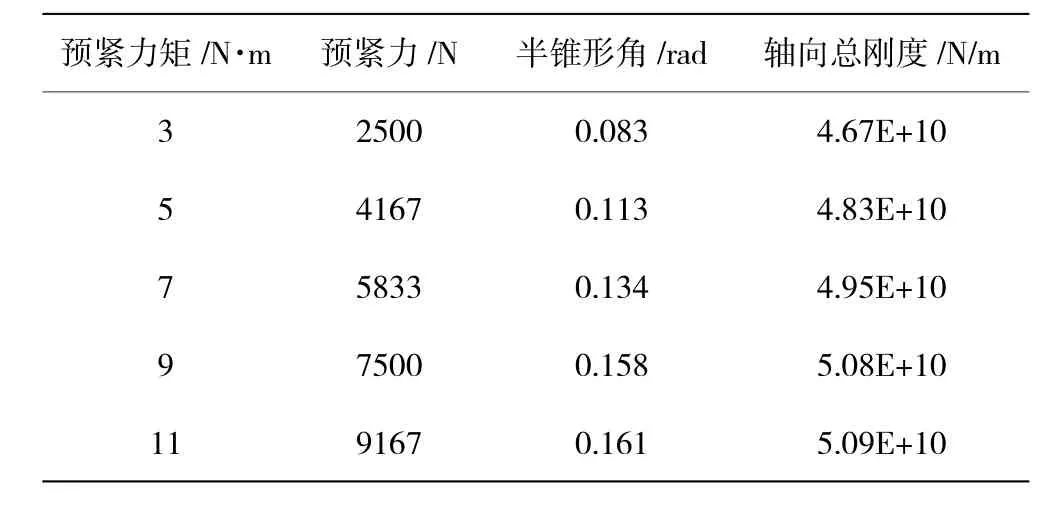
表1 不同預緊力下機匣連接件軸向總剛度

不同擰緊力矩下機匣連接件總剛度的變化如圖6所示。從圖中可見，軸向連接剛度曲線的斜率隨著擰緊力矩的增大逐漸減小，說明隨著擰緊力矩的增大，機匣螺栓法蘭連接部分逐漸趨于剛性。

2.2 螺栓連接機匣簡化

根據分區域薄層單元建模方法，去除機匣連接件法蘭邊上的螺栓孔，把螺栓等效為如圖7所示的分區域薄層單元。

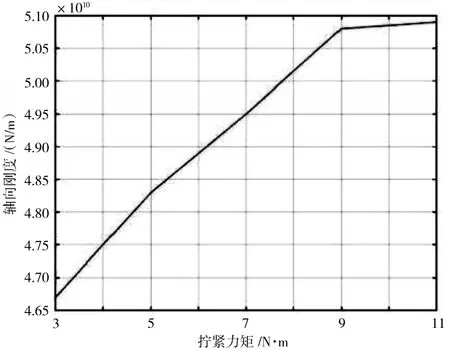
圖6 軸向剛度隨擰緊力矩的變化

最終建立的機匣連接件簡化模型如圖8所示。采用2階4面體單元，設定網格尺寸為10 mm。該簡化模型共有14萬個節點，42萬個自由度，與超模型相比，連接機匣模型規模降低到原來的1/10。

根據式（23）和式（24）確定不同預緊力下的分區域薄層單元的彈性模量，見表2。

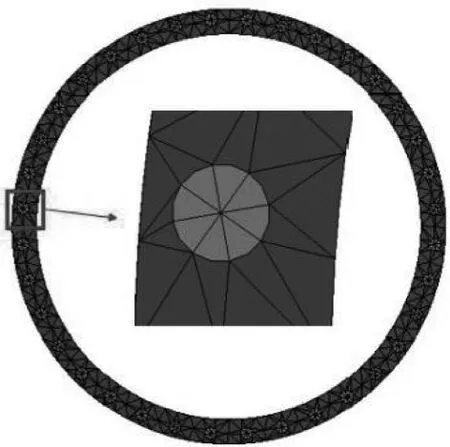
圖7 薄層單元建模

圖8 螺栓連接機匣簡化模型

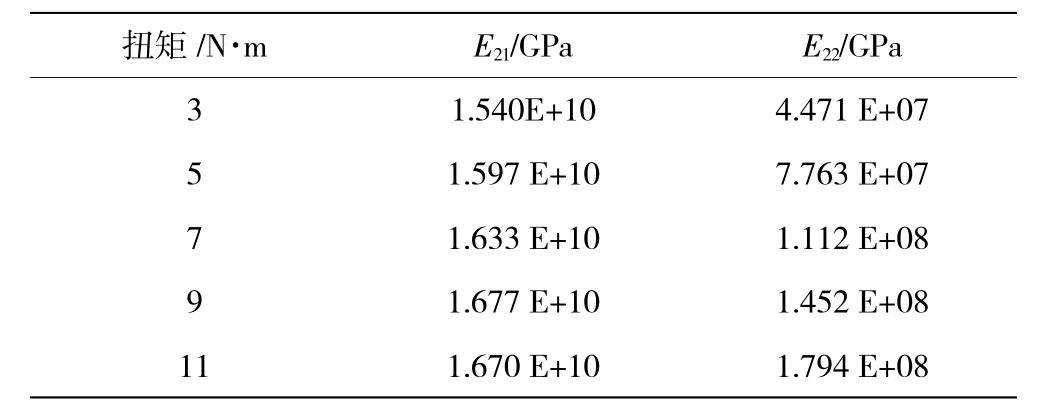
表2 薄層單元的彈性模量

圖9 連接試驗機匣模態試驗

2.3 螺栓機匣試驗測試

在連接螺栓上施加3～11N·m的擰緊力矩時，測試連接機匣的模態頻率如圖9所示。采用力錘激勵，加速度傳感器測量；采集激勵信號和響應信號，通過頻響分析軟件對測得的頻響函數進行分析，并提取連接機匣前8階頻率。

2.4 結果對比

在螺栓擰緊力矩分別為3、7、11 N·m時，分區域薄層單元模型仿真頻率與機匣試驗頻率見表3。從表中可見，連接機匣試驗頻率隨著擰緊力矩增大而加快，第3、4階頻率變化最為明顯，說明螺栓預緊力大小對連接機匣的動力學響應有較大影響。簡化模型仿真頻率與機匣試驗頻率相比，最大誤差僅為2.83%，滿足工程設計要求。由此可見，分區域的薄層單元建模方法能準確地模擬在不同預緊力下螺栓連接結構的剛度變化，建立有效的連接結構有限元模型。

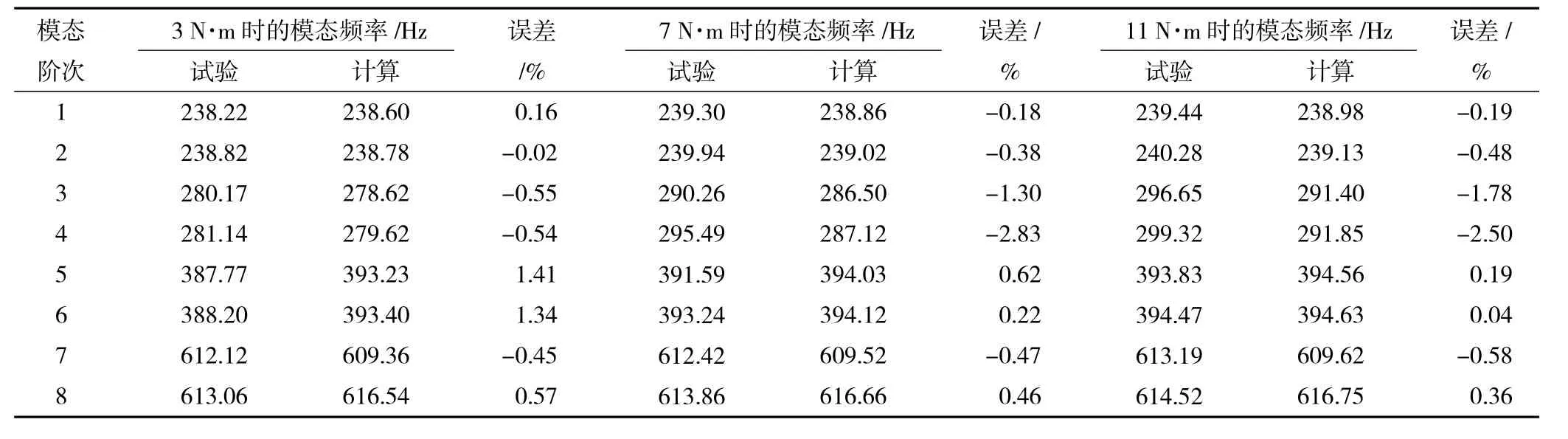
表3 在擰緊力矩為3、7、11 N·m時分區域薄層單元簡化模型的模態頻率

3 結論

本文基于螺栓連接超模型的剛度理論、赫茲接觸理論以及M-B分形模型，考慮螺栓的數量和法蘭邊的接觸，建立了分區域薄層單元的螺栓連接簡化建模方法，推導了不同預緊力下分區域薄層單元彈性模量的計算公式。通過模態試驗驗證了不同螺栓預緊力簡化建模方法的正確性，得到如下結論:

螺栓預緊力對機匣連接部分的法向接觸剛度影響較大，隨預緊力的增大，法向接觸剛度增加，之后逐漸趨于平穩；連接機匣的各階固有頻率也逐步加快，之后也趨于平穩。

本文連接接觸的建模，沒有考慮連接接觸非線性阻尼的影響，但為進一步在此方面深入探索螺栓連接動力學的問題奠定了基礎。