以“不變”應(yīng)“萬變”

江蘇省蘇州市陽山實(shí)驗(yàn)初級(jí)中學(xué)九（9）班 許辰宇

【問題背景】已知y關(guān)于x的函數(shù)表達(dá)式y(tǒng)=2kx-3k+2，觀察這個(gè)函數(shù)表達(dá)式，你有什么發(fā)現(xiàn)？

面對(duì)這個(gè)問題，一開始或許你毫無頭緒，仔細(xì)思考后，可能你會(huì)有所發(fā)現(xiàn)，甚至發(fā)現(xiàn)獨(dú)特之處。

【思考探索】不難發(fā)現(xiàn)，這是一個(gè)含參數(shù)（k）的一次函數(shù)解析式。為了研究它的特殊性，我們不妨取一些k值（如表1），并畫出它的圖像（如圖1）。

表1

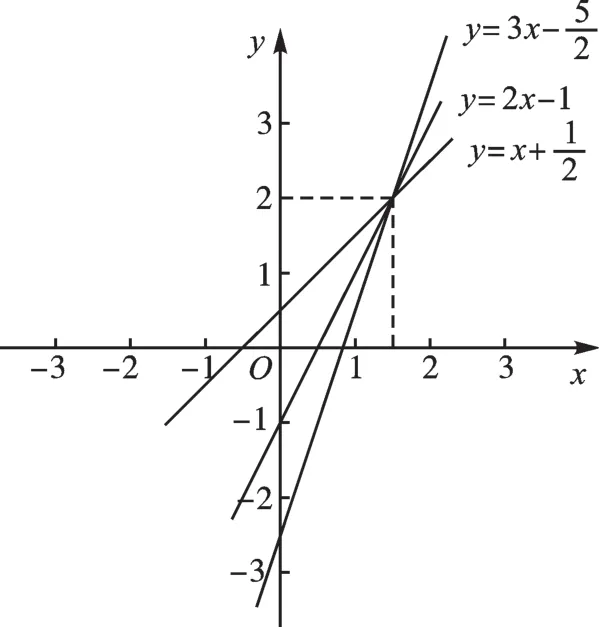
圖1

觀察圖像，我們可以得知，一次函數(shù)y=2kx-3k+2的圖像總經(jīng)過點(diǎn)（，2）。這是什么原因呢？于是，我對(duì)原來的表達(dá)式進(jìn)行恒等變形，看看能否找到問題的答案。

由y=2kx-3k+2，可得y=k（2x-3）+2，即y-2=k（2x-3）。

既然原函數(shù)表達(dá)式y(tǒng)=2kx-3k+2是成立的，那么變形后的表達(dá)式也是成立的，而我們知道，k作為一個(gè)系數(shù)是可以取不為0的任何實(shí)數(shù)的，要使原式成立，需滿足（y-2）和（2x-3）的值分別為0。這就是為什么函數(shù)圖像總經(jīng)過點(diǎn)（，2）的本質(zhì)原因。

結(jié)論應(yīng)用如圖2，在平面直角坐標(biāo)系xOy中，以原點(diǎn)O為圓心的圓過點(diǎn)A（13，0），直線y=kx-3k+4與⊙O交于B、C兩點(diǎn)，則弦BC的長(zhǎng)的最小值是多少？

本題是一道有關(guān)線段最值的問題。在圓內(nèi)求線段的最值，需確定線段的兩個(gè)端點(diǎn)的位置。從這個(gè)角度分析，即使我們知道k值，也很難確定點(diǎn)B與點(diǎn)C在平面直角坐標(biāo)系中的位置。因此，我們要從函數(shù)表達(dá)式入手，將其進(jìn)行適當(dāng)?shù)淖冃危l(fā)現(xiàn)函數(shù)圖像總過點(diǎn)（3，4），此時(shí)可求得圓心O到點(diǎn)（3，4）的距離為5，問題就轉(zhuǎn)化成求過⊙O內(nèi)一點(diǎn)的最短弦問題。運(yùn)用垂徑定理和勾股定理，求解步驟如下：

解：∵y=kx-3k+4，

∴k（x-3）=y-4，

∵k有無數(shù)個(gè)取值，由x-3=0、y-4=0，

可得x=3，y=4，

∴直線一定過點(diǎn)D（3，4）。

如圖3，根據(jù)勾股定理，可求得OD=5。

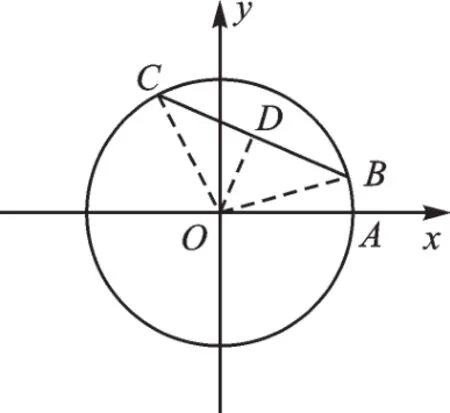
圖3

∵最短的弦BC是過點(diǎn)D且與⊙O垂徑垂直的弦，∴連接OC，OC=OA=13，OD=5，在Rt△COD中，可求得CD=12。

∵OD⊥BC，

∴BC=2CD=24。

【解題感悟】在求解有關(guān)含參數(shù)的函數(shù)表達(dá)式的問題時(shí)，往往需要在變化的參數(shù)中找到那個(gè)“不變”的點(diǎn)（或量），再運(yùn)用這些不變的量去破解復(fù)雜多變的問題，此所謂以“不變”應(yīng)“萬變”。

教師點(diǎn)評(píng)

此文“結(jié)論應(yīng)用”中呈現(xiàn)的題目來源于某次調(diào)研試卷，是一道一次函數(shù)與圓相結(jié)合的綜合題，所給一次函數(shù)解析式為“含參型”解析式。在講評(píng)此題時(shí)，許辰宇同學(xué)展示了自己的解法，從“數(shù)式”的視角做了詳細(xì)的分析。對(duì)于該題，一部分同學(xué)理解并掌握，但仍然有部分同學(xué)不太理解，尤其是怎么得到“定點(diǎn)”的。課后他將此題整理成文，從“表格”“圖像”“數(shù)式”的全方位視角作了精彩分析，讓同學(xué)們對(duì)此類“含參型”一次函數(shù)過“定點(diǎn)”的本質(zhì)有了更深刻的認(rèn)識(shí)。這篇文章從問題提出、問題分析、問題解決和問題反思4個(gè)環(huán)節(jié)展開，結(jié)構(gòu)優(yōu)美，言之有物，思考深刻，值得借鑒。