建模序列數乘變換下的DDGM(1,1)模型參數特性

馬紅燕，崔 杰,2，王 雨

（1.淮陰工學院 商學院，江蘇 淮安 223001；2.南京航空航天大學 灰色系統研究所，南京 210016）

0 引言

20世紀90年代初，中國學者鄧聚龍教授提出了灰色系統理論（簡稱灰理論）。該理論以“部分信息已知，部分信息未知”的“小樣本”“貧信息”不確定性系統為研究對象，通過對部分已知信息的生成、開發，提取有價值的信息，從而對系統結構性質、演化規律進行正確描述與有效監控[1-3]。目前，灰理論在農業、工業、國防、科技、軍事、教育、醫療等眾多領域具有廣泛的應用空間，已為經濟和社會發展發揮了重要推動作用。現有研究表明，在灰建模前對系統原始特征序列進行數據變換，有利于簡化建模過程[4-7]。目前，學術界部分學者對灰預測模型建模序列數乘變換前后的參數變化特征進行了研究，并取得了豐碩成果[8-14]。研究結果顯示，對部分灰預測模型而言，在建模前對系統特征序列進行線性變換，可降低其建模復雜性。

灰預測是灰理論的重要分支之一。灰色GM(1,1)預測模型一直倍受學者們關注，同時亦是應用最為廣泛的灰色模型之一。然而，該模型在實際應用中卻時常出現預測精度不穩定的問題。目前眾多文獻對其進行的深入研究結果顯示，該模型以差分方程建模為基礎進行參數估計，而用來預測的時間響應函數卻是由相應微分方程的解引申得到，從差分方程到微分方程的跨越缺乏科學依據和理論基礎。鑒于此，謝乃明等[15]提出了DGM(1,1)模型，解釋了GM(1,1)預測精度不穩定的主要原因，并對DGM(1,1)模型的參數進行了優化研究。然而，DGM(1,1)模型依然是基于累加的方式尋找蘊含在序列中的灰指數規律，以解釋系統未來的發展趨勢。而在已知建模序列為近似齊次指數序列前提下，對該序列進行累加生成往往會破壞其原有規律，降低建模精度。因此，曾波等[16]在DGM(1,1)模型基礎上，提出了直接DGM(1,1)模型（簡稱DDGM(1,1)模型），并通過實例證明了該模型的有效性。由于DDGM(1,1)模型提出時間尚短，關于該模型參數特性的研究成果十分缺乏。研究其參數特性有利于進一步拓展DDGM(1,1)模型的應用范圍，簡化該模型的建模過程，提高其建模效率。鑒于此，本文以DDGM(1,1)模型為研究對象，利用三級參數包技術分析了該模型建模參數在系統特征序列經數乘變換前后的數量關系，進而揭示了該模型精度在建模序列經數乘變換前后的變化規律。

1 DDGM(1,1)模型的建模原理

定義1：設系統原始特征非負序列X(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}，則：

式（1）為直接DGM(1,1)模型，簡稱DDGM(1,1)模型[16]。

定理2：設B、Y、如定理 1所述，取則：

（1）稱 (β1，β2)為DDGM(1,1)模型的一級參數包，記作PI：

（2）稱 (β1，β2)的構成成分為DDGM(1,1)模型的中間參數，其全體構成該模型的二級參數包，記作PII。

（3）稱DDGM(1,1)模型的二級參數包的構成成分為基本參數，其全體構成該模型的三級參數包，記作PIII。

命題1：DDGM(1,1)模型的一級參數包PI在最小二乘準則下有如下矩陣算式：

其中：

命題2：令：

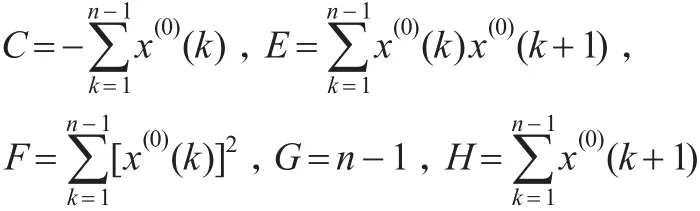
則有：

命題3：DDGM(1,1)模型的參數包有：

（1）一級參數包

（2）二級參數包

（3）三級參數包

2 DDGM(1,1)模型的參數特性

定義2：對于系統原始非負數據序列Xk，Yk=ρXk，k=1，2，…,n;(ρ為常數，且ρ＞0)稱為數乘變換，其中ρ為數乘量。

設X(0)=(x(0)(1)，x(0)(2)，…，x(0)(n))為系統原始非負特征數據序列，Y(0)=(y(0)(1)，y(0)(2)，…，y(0)(n))為其經數乘變換后的序列。ρ為數乘量，且：

記 (β1，β2)為利用序列X(0)構建的 DDGM(1,1)模型參數序列為X(0)經數乘后的序列Y(0)構建的DDGM(1,1)模型參數序列，其他參數的定義類似。

定理3：二級參數包PII為：

則有:

證明：

得證。

定理 4：記 (β1，β2)為利用系統特征序列X(0)構建的DDGM(1,1)模型中的參數序列，(βˉ1，βˉ2)為利用其數乘序列Y(0)構建模型對應的參數序列，則：

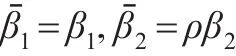
證明：

證明：

故：

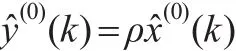
定理6：記ε(k)與εˉ(k)分別為由序列X(0)與Y(0)構建的DDGM(1,1)模型的相對誤差，即：

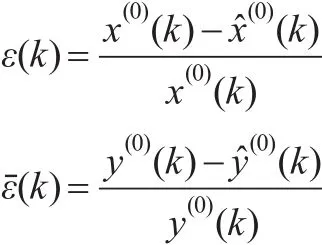
則有：

證明：

由定義2與定理5可得：

3 實例分析

設系統特征序列X(0)=(1.2，3.0，4.2，5.0，6.0，7.2)。由式（2）和式（3）可得：

由式（4）可得：

當數乘量ρ=0.5時：

因此：

上述計算結果進一步佐證了本文的結論。

4 結束語

本文采用參數包技術對DDGM(1,1)模型建模序列經過數乘變換前后模型建模參數的量化關系及其精度變化規律進行了深入研究。結果表明，DDGM(1,1)模型的精度與其建模序列的數乘變換無關，該模型的建模精度不會因其建模序列受數乘變換作用而發生變化。因此，在DDGM(1,1)模型建模過程中，可對系統特征序列進行數乘變換預處理，進而在不改變模擬與預測精度的前提下簡化其建模過程。