基于一般灰數的灰靶決策模型拓展與應用

劉中俠,劉思峰，蔣詩泉

（1.南京航空航天大學 經濟與管理學院，南京 210016；2.銅陵學院 財稅與公共管理學院，安徽 銅陵 244000）

0 引言

灰靶理論最早是由灰色系統理論創始人鄧聚龍教授提出，其基本思想是在決策模型中含有灰元或在一般決策模型與灰色模型相結合的情況下，從一組模式序列中，找出最靠近子命題目標值的數據,構造標準模式，各模式與標準模式一起構成灰靶，標準模式即是靶心。每個灰關聯差異信息空間中的模式與靶心的灰關聯度稱靶心接近度，簡稱靶心度，并提出灰靶變換。繼鄧聚龍之后，劉思峰在灰靶決策模型中利用靶心距的數值反映了局勢效果向量的優劣[1]。在鄧聚龍和劉思峰已有的研究基礎上，陸續有相關學者對灰靶決策進行深入研究和擴展[2-6]。文獻[7,8]從決策者指標滿意域和風險態度對群體決策的影響視角，提出了基于前景理論的三參數區間灰數群體灰靶決策模型，該方法充分考慮了專家關于各屬性的心理期望灰靶和決策風險態度。文獻[9]針對指標值為區間數的情形，把灰靶決策模型由實數序列推廣到區間數序列，建立了基于區間數的灰靶決策模型。文獻[10]通過比較指標集中各指標值與靶心連線所圍成圖形的面積大小來對決策方案的優劣進行評價，從而在一定程度上弱化了建模對象中極端指標值對靶心距計算結果的影響,建立了蛛網灰靶決策模型。文獻[11,12]提出了沖突利益主體不完全確定權重信息情景下的群決策方法和基于區間數的多時點多屬性灰靶決策模型，針對多屬性決策的不確定性和多時點性，利用隸屬度對案例進行排序，旨在對決策方案的排序進行優化。文獻[13]結合層次分析法和離差最大法確定指標權重，提出了多指標灰靶決策的靶心貼近度法，該方法是對加權灰靶決策的一種改進。本文在已有的研究成果基礎上，將灰靶決策理論從實數和區間灰數推廣到一般灰數，針對一般灰數灰靶決策方法的不足，給出一般灰數的概念及其距離計算公式。運用多目標線性規劃的理論給出確定指標權重的優化方法，依據灰靶決策思想，對目標屬性值和方案值均是一般灰數的決策方案，構建了基于一般灰數的灰靶決策模型，在一定程度上拓展了灰靶決策理論。

1 一般灰數的基本概念

在現實問題中，由于多種原因會使得決策信息表現為復雜性和不確定性，為了準確地表示復雜不確定信息。在灰理論的思想的指導下，將區間灰數的概念和距離測度進行了拓展，這些研究將為灰關聯與灰靶等決策模型提供了堅實的理論基礎。

定義1[1]：設則稱g±為一般灰數。其中任一區間灰數，滿足且分別稱為g±的下界和上界。

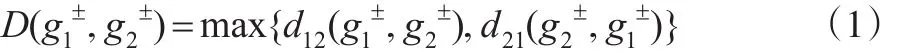
2 基于一般灰數的灰靶決策模型構建

基于一般灰數處理方法和灰靶決策模型的構建機理的角度，下面分別依次論述模型構建算法和步驟。

2.1 決策矩陣規范化處理

設skj為方案k的第j個指標值，該值為一個一般灰數，即，其中k=1，2，…，l；j=1，2，…，m。

（1）若skj為效益型指標，則規范化算子為，其中

（2）若skj為成本型指標，則規范化算子為，其中

2.2 靶心和靶心距的確定

2.3 計算投影一致性系數

定義5：稱PrjA-A+(A-Ai)表示方案Ai與負靶心連線在正負靶心連線上的投影值；PrjAi+A(A-A+)表示正負靶心連線在方案Ai與正靶心連線上的投影值，其計算公式分別為

定理1：PrjA-A+(A-Ai)越大，方案Ai越靠近正靶心A+；越小，方案越遠離正靶心越大，則方案Ai越靠近負靶心A-，PrjA+Ai(A-A+)越小，方案Ai越遠離負靶心A-。

證明：（略）。

定理2：設PrjA-A+(A-Ai)與PrjAi+A(A-A+)如定義6所示，設，其中γi為一致性系數，則，且一致性系數γi越大說明第i方案越好。

證明：（略）。

定義6：稱ψi=Ri--Ri+為靶心距得分函數。其中，Ri+表示第i個方案到正靶心的正靶心距，Ri-表示第i個方案到負靶心的負靶心距。其中，ψi值越大表明方案越優，值越小表明方案越劣。

定義7[14]：TODIM方案排序法，方案Ai相對每個方案Aj相對優勢度，其中：

在上述優勢度的計算公式中，Φc(Ai，Aj)表示方案Ai相對方案Aj在屬性C下的優勢度，參數θ是衰退系數，其值越小，表示決策者損失規避程度越高。最后計算方案Ai的全局優勢度根據ξi的大小對方案進行排序，ξi越大，方案方案越好。

2.4 指標權重的確定

設指標權向量為w=(w1，w2，…，wm)T，根據灰靶決策模型的效果向量測度準則，建立以下權重確定的多目標最優化模型：

3 基于一般灰數的灰靶模型決策步驟

步驟1：決策信息規范化處理；

步驟2：正負靶心確定；

步驟3：依2.4確定權重，計算靶心距和靶心距得分函數；

步驟4：計算投影值；

步驟5：計算灰靶決策一致性系數γi；

步驟6：TODIM法計算方案全局優勢度；

步驟7：方案排序。

4 案例分析

某投資銀行準備對一個企業進行投資，通過第一輪篩選后，還剩最后三家企業，現要在這三家企業A1、A2、A3中選擇一家，其評價指標分別為：S1表示企業年產值（千萬元）；S2表示企業社會效益（千萬元）；S3表示對環境污染程度，指標權重為W=(w1，w2，w3)經專家評價三個指標的權重范圍為w1∈[0.1，0.2]，w2∈[0.2，0.3]，w3∈[0.3， 0.5]，具體指標數據見表1。試確定銀行的最佳投資方案。

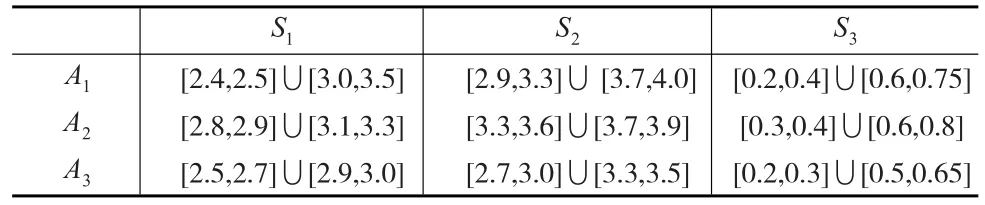
表1 決策矩陣

步驟1:信息規范化處理（見表2）。

表2 規范化決策矩陣

步驟2:確定正負靶心。

步驟3：根據2.3確定權重，計算靶心距和靶心距得分函數值。

（1）計算指標權重

求解最優化問題：

解得：W=(0.2,0.3,0.5)。

（2）計算靶心距

根據定義4，分別計算正負靶心距。

（3）計算靶心距得分函數值

根據定義6，計算靶心距得分函數值。

步驟4：計算投影值。

步驟5：計算灰靶決策一致性系數γi。

步驟6：基于TODIM方法計算方案全局優勢度。

步驟7：三種方法的方案排序。

表3 不同方法結果比較

為了說明該模型的優越性，將本文排序法同靶心距得分函數方法進行比較，本文方法排序是A2＞A1＞A3而靶心距得分函數排序也為A2＞A1＞A3這兩種方法排序完全一致。充分說明本文方法排序的合理性。將本文方法同TODIM法比較，TODIM法方案排序A1＞A2＞A3，排序結果是不盡相同，因為采用的TODIM法排序默認衰退系數θ=1，而TODIM法衰退系數取值的不同會影響方案的排序結果。而本文方法則不受其他主觀因素干擾，所以排序的可信度更高，綜上可以看出，與TODIM法比較而言本文方法的排序結果更值得信賴。

同時，由于決策環境信息的復雜不確定性，所以決策者只能以一般灰數的形式給出決策信息，此時很難根據現有的灰靶決策方法進行決策。而基于一般灰數的灰靶決策模型就能很好地解決這一問題，該模型是考慮方案與正、負靶心之間的距離關系，通過在改變投影方向并結合相對貼近度的思想，并利用多目標優化模型給出一種確定指標權重的方法，構建了基于一般灰數的灰靶決策模型。本文給出的案例充分說明該法對排序更加科學合理。

5 結束語

本文針對信息為一般灰數的決策問題進行了系統研究。首先，利用一般灰數來表征復雜不確定信息。其次，給出了一般灰數的距離定義。再次，利用灰靶決策的思想和相對貼近度的思想，提出了基于一般灰數的灰靶決策拓展模型，該模型有效地解決了復雜不確定信息的決策問題，其最大優點是有效解決策信息為復雜不確定性的一般灰數時，難以精確排序問題。最后，通過實際案例充分說明該模型的科學合理性，為復雜不確定信息下決策問題的研究提供了一個新的研究視角。