考慮導彈速度時變的帶落角約束制導律*
龍婧,孔哲,潘濤
(西安航天動力技術研究所,陜西 西安 710025)
0 引言
隨著現代戰爭作戰需求的多樣化,以及固體變推力發動機技術的發展,小型戰術導彈將具有一定程度的自主變速能力,因此在進行末制導律設計時應同時考慮速度變化。但目前大多數基于比例導引律[1-4]、最優制導律[5-8]以及滑模變結構制導律[9-12]而展開的落角約束末制導律研究均假定導彈速度恒定,關于速度時變的研究較少。現有的幾篇文獻中,馬國欣[13]等將導彈的速度信息視為是部分先驗已知的,通過對導彈速度曲線進行預測并根據當前時刻測得的實際速度大小對其進行更新,從而得到了導彈速度的變化規律。Taub[14]對預測的速度不斷進行數值迭代獲得了接近實際的速度變化規律,并基于最優控制極小值原理推導出了落角約束末制導律。這2篇文獻都將速度預測為時間的函數,實際過程中需要不斷進行更新或者迭代,增加了推導過程的難度。
本文直接將導彈速度假設為相對距離的指數函數,通過建模引入了脫靶量和落角約束,根據最優控制原理直接求解黎卡提方程,獲得了考慮速度時變的帶落角約束的制導律解析表達式。仿真表明,該制導律能夠滿足設計要求,并可以適用于不同速度變化的情形,相比傳統的最優彈道成型末制導律具有更平直的彈道和更小的需用過載。
1 問題描述與建模
首先進行以下假設:①導彈和目標均視作質點,在二維平面內運動,且目標靜止;②忽略導彈和目標受到的重力作用;③末制導階段導彈速度矢量與彈目連線之間的夾角為小量。末制導段彈目相對運動如圖1所示。
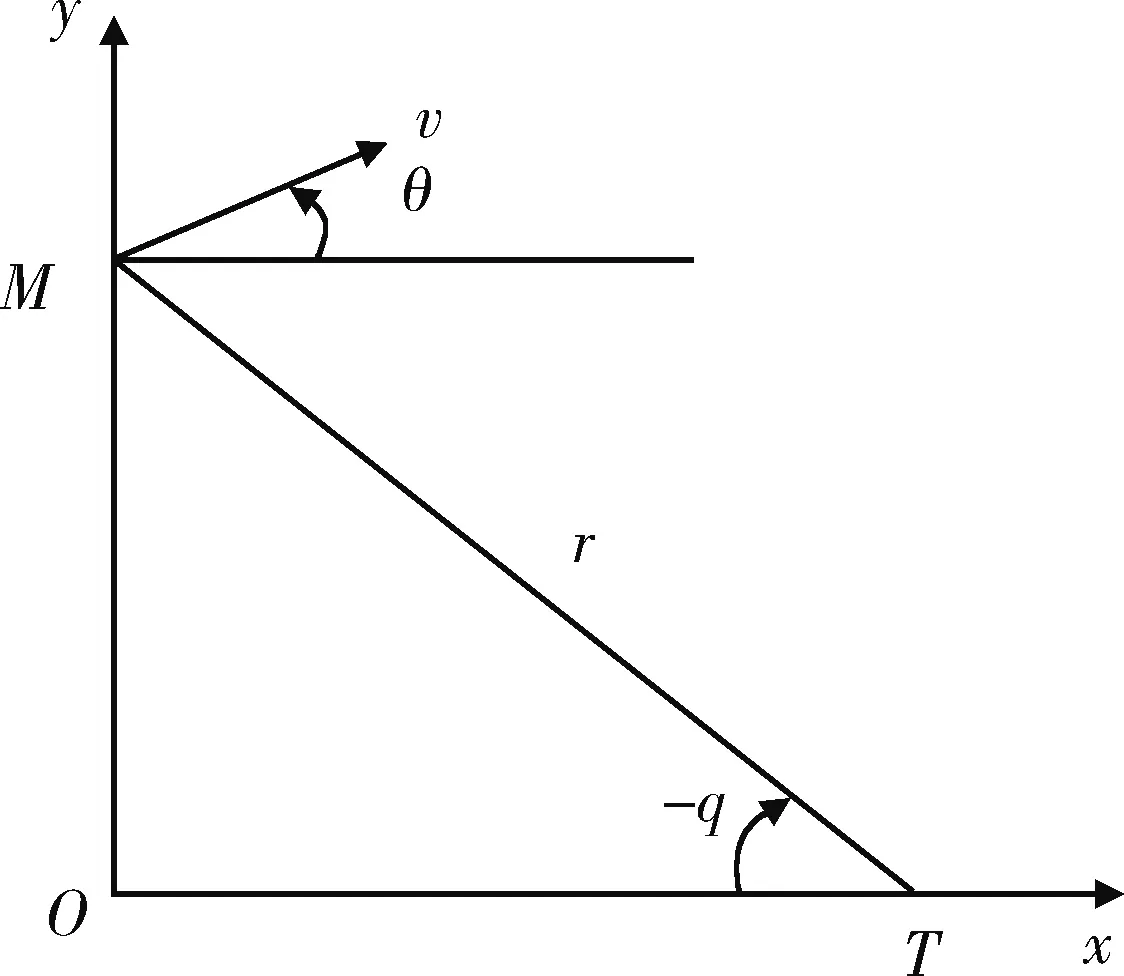
圖1 彈目相對運動關系圖Fig.1 Relative motion relationship betweenmissile and target
圖1中,M代表導彈位置,T代表目標位置。r,q,θ分別為彈目相對距離、目標視線角以及導彈的彈道傾角,v為導彈當前時刻的速度。
相對運動方程可以描述為
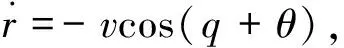
(1)
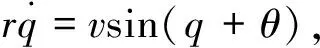
(2)
對式(2)求導并聯立式(1)可得
(3)
為了滿足脫靶量以及末端落角約束,選取狀態變量如下:
(4)
式中:θd為導彈的期望落角。
則上述問題可以表達為系統狀態方程的形式:
(5)
終端約束條件為x1(tf)=0,x2(tf)=0。
選擇二次型性能指標如下:
(6)
式中:R為對稱正定矩陣;F為半正定對稱矩陣。選取R=1,F-1=0,將導彈末端約束問題轉化為典型的最優控制問題。
2 最優制導律設計
根據最優控制理論[15]可知,第2節描述的問題的最優解存在且唯一,即
u*=-R-1BTPx,
(7)
式中:P為滿足黎卡提方程的對稱矩陣,可以通過求解逆黎卡提方程得到。
逆黎卡提方程如下:
(8)
令
(9)
由于P為對稱矩陣,q12=q21。
則式(8)可以寫為
(10)
即
(11)
將式(11)展開后可得
(12)
假定導彈在制導過程中的速度可控,并可近似寫成彈目相對距離r的指數函數的形式,如式(13)所示:
v=kra,
(13)
式中:k和a為常數,且滿足k>0,a<0。當導彈速度為常值時,a=0。對式(13)求導可得速度變化率為
(14)
此外,根據第1節假設(3)可得
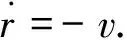
(15)
聯立式(12)~(15)求解即可得到矩陣Q如下:
(16)
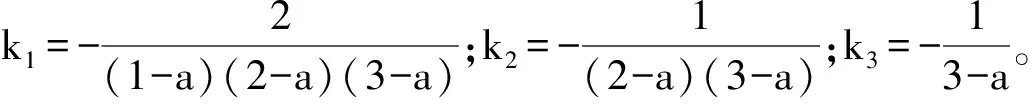
P=Q-1=
(17)
將k1,k2,k3代入式(17)中,則
(18)
將式(7)展開,代入矩陣B,P,x,最終可以得到
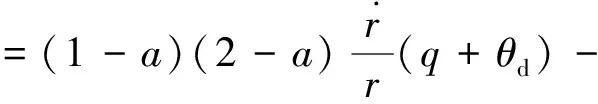
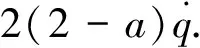
(19)
最優制導律為
(20)
當a=0時,導彈速度為常值,導引律為
(21)
與文獻[5]中給出的相同。
1.1 對象 選擇2011年1—12月在我院行前列腺電切術患者40例為觀察組,年齡53~79歲,平均年齡68.0歲,實施臨床護理路徑方法;以2010年1—12月在我院行前列腺電切術患者40例為對照組,年齡在56~81歲,平均年齡71.0歲,采用常規護理方法。入選條件:診斷明確,沒有嚴重的合并癥,且患者能配合完成各項治療和護理。兩組患者在年齡、文化程度等比較差異無統計學意義(P>0.05),具有可比性。
3 仿真分析
設初始時刻導彈的坐標為(0,4 000m),目標的坐標為(3 000 m,0)。初始時刻導彈的彈道傾角為0,導彈的期望落角為-60°。
(22)
3.1 仿真校驗
為了研究不同速度變化情況下本文提出制導律的性能,在上述仿真條件下,分別取a=-0.2,k=550;a=-0.6,k=16 500;以及a=-1,k=500 000進行仿真,結果如圖2所示。
仿真結果表明,在初速相同,導彈采用不同的加速度飛向目標的條件下,本文給出的制導律都能夠以要求的落角擊中目標,導彈軌跡以及彈道傾角變化較為平緩,法向過載較小,而且在彈道末端導彈的法向過載有趨于0的趨勢。因此,本文提出的制導律有效且具有良好的綜合性能。
3.2 與傳統最優制導律對比
為了研究本文給出的末制導律與傳統的最優末制導律即式(20)與式(21)的區別,進行了如下仿真。
其次對速度曲線的不同擬合情況進行對比。由圖3d)可以看出,擬合速度1的精度高于擬合速度2,所以制導律1相比制導律3具有更平緩的彈道和更小的法向過載,但二者差距并不明顯,這說明速度曲線擬合精度要求不必太高。
綜上,在較大的擬合精度范圍內,本文給出的制導律都具有高于傳統最優制導律的綜合性能,因此,當導彈速度時變時,可以用速度關于相對距離的指數函數對導彈預設的速度曲線進行擬合,并根據式(20)得到性能良好的制導律。
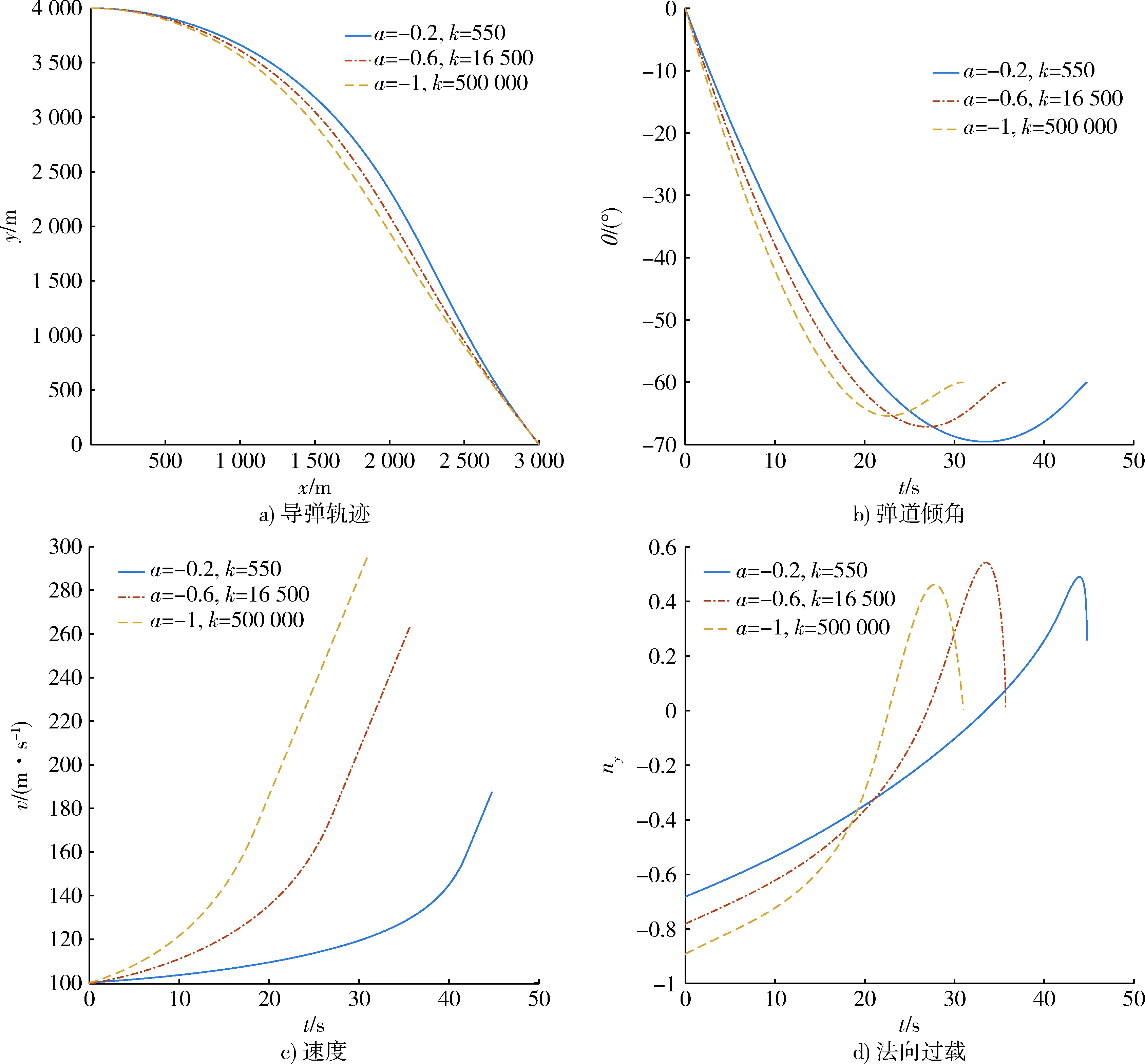
圖2 不同參數條件下的仿真結果Fig.2 Simulation results with different parameters

圖3 勻加速情況下最優制導律對比Fig.3 Comparison of optimal guidance law with constant acceleration
4 結束語
本文根據小型戰術導彈可能具有的自主變速能力,提出了速度時變條件下滿足脫靶量和落角約束的最優制導律。仿真結果證明了推導中各個假設的合理性以及該制導律的有效性。所設計的制導律結構簡單,精度良好,適用范圍廣,具有一定的工程應用價值。

