目標RCS特性的仿真可信度評估方法及應用*
孫碧晴,王旭
(北京理工大學 信息與電子學院,北京 100081)
0 引言
作為一種可以在非試驗環境下,對目標進行模擬的技術,目標仿真技術已深入到科學研究和工程應用的許多領域。外場試驗消耗人力物力,因此在非必須做外場試驗的情況下,采用仿真系統對目標特性進行模擬是一種較優的替代方案。針對目標RCS特性仿真技術是模擬仿真技術與雷達技術相結合的產物,它可以通過算法推導或是搭建實物平臺,對目標RCS特性進行模擬。隨著仿真技術的不斷發展和對仿真系統需求的不斷增長,仿真系統的可信度成為了關注的焦點,它體現了仿真系統與被仿真真實系統的一致性程度,表征了仿真系統的使用者對應于仿真試驗的結果解決某個特定問題的正確性的信任度[1]。
然而,針對雷達的評價系統大多對于雷達性能評估[2-3],對于目標RCS特性仿真的可信度評價方法的研究尚未充分進行。為此,本文研究了仿真系統可信度評估方法,并對其進行改進,最終應用于雷達目標特性仿真系統的可信度評估工作中。
基于相似學的仿真系統可信度評估方法通過計算仿真系統與原型系統的相似度,得到仿真系統的仿真可信度[4]。目前常用的相似度計算方法[5-7]具有局限性:沒有考慮到數據序列之間的相關性,因此在數據序列趨勢不一致的情況下給出的相似度結果并不合理。在數據相關的條件下對數據的相似度進行計算則更有意義,因此本文給出了相關相似度的概念作為相似度的改進方法,參與仿真系統的可信度評估。
本文首先簡要介紹了仿真系統可信度分析方法及相似學原理,并結合現有技術,提出了基于相關性分析的仿真系統相似度算法以及運用灰色綜合評價法確定仿真權重的方法,以實現對目標RCS特性模擬系統的可信度評估,并給出了相應評估模型,最后對實例進行評估并給出結果。
1 可信度分析對象與分析方法
根據仿真系統的評估對象不同,可信度評估工作主要分為2類:一是分析仿真結果是否與理論值或期望值一樣,即分析結果的逼真度;二是驗證模型行為特性與系統行為特性的對比精度滿足仿真目的規定的要求,也就是判斷模型的有效性[8]。
根據仿真系統可信度評價的原理,可信度評估可以分為定性、定量和定性定量綜合等3類方法[1,5]。定性方法簡便直觀,但具有較強的主觀性;定性與定量綜合方法適合解決復雜系統的可信度評價問題,在一定程度上仍存在定性評價的主觀性問題;定量評價的方法是以相似學原理為基礎,通過數學手段對評價策略進行描述,給出仿真系統與實際系統之間的一致性結果,較好地解決了前面2種方法的缺點。
本文討論的可信度評估方法是以仿真系統輸出結果的逼真度為評估對象,基于相似學原理,對仿真數據和參考數據(實測數據)進行定量評價的,并可以推廣到其他基于輸出結果的仿真系統可信度評估情景中。
2 可信度的定量評價模型
2.1 相似學原理
系統A由k個要素組成,系統B由l個要素組成,系統A與B有m對相似要素(相似元),每對相似元的相似程度記為q(ui),系統間的相似度記為Q,則相似系統的數學模型可描述為
Q=f(k,l,m,q(ui)), 1 系統相似度為 (1) 式中:m/(k+l-m)表示系統A與B之間相似要素數量m對系統相似度的影響;βiq(ui)表示每一相似要素的相似程度及其權重對系統相似度的影響;相似度q(ui):0≤q(ui)≤1。 (2) 數據序列長度為n的2組數據序列的相似度為 (3) (4) 上述計算相似度的方法不能識別2組數據變化趨勢的一致性程度,因而不能識別數據序列極性,進而不能給出合適的相似度值。本文提出了相關相似度的概念來描述數據的相似性,來解決上述問題。 通過以上的分析可知,在數據變化趨勢一致的條件下計算數據相似度更有實際意義。我們將2組數據之間的趨勢一致性程度稱為它們的相關度。假設一對待評估系統中的某相似元可以用具有n個值的序列x描述,2個系統對應的序列x1與x2之間具有k個趨勢相關點,則x1與x2的相關度為 (5) 利用相關度對相似度進行調節,得到2個數據序列的相關相似度。將式(5)代入式(4),得到2組數據序列的相關相似度為 ξ(ui)=q(ui)ri. (6) 相似元的相關相似度ξ(ui)可以視為其相似度q(ui)的一種優化解,因此在評估系統間的相似度(可信度)Q(A,B)時,可以用相關相似度ξ(ui)替代相似度q(ui)參與計算。 目前文獻介紹最多的相似要素權重確定方法是AHP層次分析法[6-7,9-13]。其權重的確定需要經過專家團根據具體系統特征給出評判結果[1,12-13],會受到很大程度的主觀影響,且適應性差。 采用灰色綜合評價法來判斷各個相似要素的權重。該方法可以很好解決權重評定的主觀性和適應性差的問題[14-15]。 建立灰色關聯。{x0,x1,…,xm}為因子集。其中x0為參考序列;xi為仿真系統輸出的參數數據序列;i=1,2,3,…,m。 參考序列之初值項: (7) 各點之絕對差值: (8) 兩極最大差與最小差: (9) (10) 計算關聯系數: (11) 式中:ζ為分辨系數,且ζ∈(0,1),通常取ζ=0.5。 計算關聯度: (12) 對得到的各因素關聯度進行歸一化,求各因素所占的權重: (13) 仿真試驗過程中,要求仿真系統A和實際系統B的相似要素(輸出參數)的個數相同,且每個參數對應的數據序列等時距、等長度。 式中:n為序列長度;i=1,2,3,…,m為仿真系統輸出參數的個數。 綜上所述,采用式(1)計算得到仿真系統的綜合可信度時,仿真系統和實際系統的相似要素個數相同,即k=l=n,則系統間的可信度為 (14) 對于式(14),當Q=0時,仿真系統與實際系統之間沒有任何相似的地方;當0 第2步,采用式(5),(6)得到2組數據序列的相關相似度ξ(ui); 第3步,采用式(7)~(13)獲得各個相似要素的權重βi; 第4步,采用式(14)計算仿真系統A相對實際系統B的綜合可信度Q(A,B)。 構造3組數據序列。第1組,序列2的每個點數值是序列1每個點數值的2倍;第2組,序列2的每個點數值是序列1每個點數值的2倍且極性相反(-2倍);第3組,兩序列的關系基本隨機,其中有的點對應數據設計成0.5倍的關系,有的極性相反。各個序列的具體數值見表1。 3組數據序列的曲線分別如圖1a)~c)所示。假設V0與V00為1組相似系統的一對相似元,其中V0為理論(實測)系統的輸出結果,V00為仿真系統的輸出結果。 表1 3組數據序列的值Table 1 Values of three groups of data set 運用式(2),(4)和本文提到的相關相似度的計算方法(下文中,將這3種方法用“方法1”、“方法2”、“方法3”簡化代替),獲得上述3組數據序列相似度計算結果如表2所示。 第1組數據序列存在倍數關系,然而方法1給出的相似度為0,與實際情況不符;方法2,3計算的結果更符合情況。對于后2組數據,方法1給出的結果超出相似度取值范圍,不具有參考價值,因此下文只對比分析方法2,3處理這2組數據的結果。由于方法2不能識別數據極性,對倍數相同、極性不同的2對序列(第1,2組數據)給出了相同的結果;而由于方法3具有識別極性的功能,結果更為可靠。對比圖1c),方法2對于第3組數據的處理結果過高,而方法3的結果更為可靠。 注:第1組數據的相關度r1=1,第2組為r2=0,第3組為r4=0.368 4。 通過算例運用與對比分析,可見本文給出的相關相似度方法比較好的解決目前相似要素相似度計算方法存在的問題。 本實例對某型艦艇雷達模擬靶進行評估。該模擬靶是采用電磁計算軟件計算艦艇的RCS理論值作為輸入,設計建造的雷達模擬靶,可對目標在Ka,Ku,X波段VV,HH極化條件下的目標RCS特性進行模擬。按照本文論述的仿真系統可信度評價模型和可信度評價步驟,采用該型艦艇的RCS理論數據與外場試驗中對雷達模擬靶的量測數據作為對比,對模擬系統進行可信度評估。相應的,仿真系統的評估參數共6個,分別為Ka波段、Ku波段、X波段中目標HH極化和VV極化的RCS信息,如圖2a)~c)所示。 第1步,計算模擬靶的Ka波段HH極化結果、Ka波段VV極化結果、Ku波段HH極化結果、Ku波段VV極化結果、X波段HH極化結果、X波段VV極化結果與RCS理論值的相似度,結果為:q={0.970 7,0.978 8,0.970 9,0.982 4,0.967 3,0.968 4}。 第2步,計算模擬靶的Ka波段HH極化結果、Ka波段VV極化結果、Ku波段HH極化結果、Ku波段VV極化結果、X波段HH極化結果、X波段VV極化結果與RCS理論值的相關相似度,結果為:ξ={0.791 1,0.927 1,0.836 6,0.965 5,0.807 7,0.831 7}。 第3步,計算Ka波段HH極化、Ka波段VV極化、Ku波段HH極化、Ku波段VV極化、X波段HH極化、X波段VV極化結果在仿真系統可信度評價體系所占權重,結果為:β={0.156 9,0.173 9,0.157 3,0.178 3,0.165 9,0.167 8}。 第4步,綜合得到該模擬靶的可信度:Q=0.862 6。 近年來,針對仿真系統可信度評估問題,盡管已開展了許多研究工作,但大多集中在仿真結果的校核驗證方面,對仿真可信度評估方法的研究仍不充分。本文對此做了一些有益的嘗試,所提出的相關相似度的計算方法和基于模糊綜合的仿真參數權重的方法,通過模擬驗證和工程運用表明,方法是可行的,能夠在一定程度上解決目前有關相似度算法的局限;可以適用于目標RCS模擬器的工作實際,滿足目標仿真驗證工作需要。本文闡述的方法也可以推廣到數學仿真系統可信度評估領域。2.2 相似度的確定

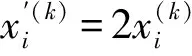

2.3 相似要素權重的確定
3 仿真系統綜合可信度評價方法
3.1 仿真系統綜合可信度
3.2 仿真系統可信度計算步驟

4 算例應用
4.1 相似度算法驗證運用

4.2 實例應用
5 結束語

