密集火力打擊目標選擇及WTA求解算法*
賈汝娜,宋貴寶,李一夫
(海軍航空大學,山東 煙臺 264001)
0 引言
美軍在《快速決定性作戰》中提出“基于效果作戰”的理論,即“對知識、計劃和作戰都有重要意義的戰爭哲學,重在戰略、戰役和戰術級使用軍事和非軍事能力以獲取所期望的戰略結果”,其理論基礎是認為“敵人是一個系統”,改變了傳統殲滅有生力量達到作戰目的的“基于摧毀的作戰”思想,強調通過影響關鍵點來控制局勢,找到攻擊的重心和關鍵弱點[1]。2003年的伊拉克戰爭體現了上述特點,美軍抓住重心巴格達城市,巧妙打擊要害,最終通過控制薩達姆指揮基地使得整個對方作戰系統崩潰。在現代作戰中,美軍的目標選擇理論有許多借鑒之處,尤其是敵我雙方戰斗力量不再懸殊巨大,作戰的兵力和武器裝備等消耗巨大,準確判斷敵方系統的重要價值目標和關鍵環節可以起到掌控戰場局勢、加速戰爭進程和減少戰爭損失的作用。
對價值目標進行密集火力攻擊,以集中火力對敵方進行摧毀性打擊是海上作戰的經典思路[2],但在實戰中不同火力發射平臺的發射準備時間和發射轉火時間存在差異,如何進行多波次打擊時火力目標分配以提高打擊效率是一個重要問題。在火力分配(weapon target assignment,WTA)的求解上,常采用的方法有精確算法和智能算法。精確算法,如目標規劃算法,動態規劃算法,可以求得問題的唯一精確解,但不適用于求解規模較大的情況;現代智能算法包括遺傳算法,粒子群算法,蟻群算法等,可以通過提高求解次數不斷尋找優化解,求解問題規模大且求解效率高[3-4]。
1 目標任務契合度計算方法
1.1 直覺模糊隸屬度函數求解目標任務契合度思路
對于敵方目標的價值判斷首先要確定目標價值的影響因素,通常包括作戰任務、戰場態勢、威脅等級、戰場環境等因素表征具體目標在整個作戰任務中的任務價值模式P[5-7]。
常見的專家等級打分法、經驗判斷法等受專家非理性因素影響較大,所以結合直覺模糊集理論,選取直覺隸屬度函數,在一定程度上規避了非理性決策行為的影響[8-10]。
對各敵方目標Gp(p=1,2,…,n),計算其與任務價值模式P的契合度,用QGp表示。選擇模糊集〈αP,βP〉表示敵方目標的任務價值,直覺模糊集〈μ,ν〉表示任務價格模式P的作戰需求,那么敵方目標Gp與作戰需求模式P的非相似程度表示為D(〈αP,βP〉,〈μ,ν〉)(0≤D≤1),而且D越小表示兩者的匹配程度越高,所以這里取QGp=1-D。模型建立過程如下。
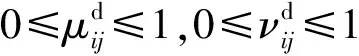
S=(sj)1×n=P(〈μ1,ν1〉,〈μ2,ν2〉,…,〈μn,νn〉).
同樣用αpj(j=1,2,…,n)表示敵方目標Gp關于A={a1,a2,…,an}的隸屬程度,用βpj(j=1,2,…,n)表示敵方目標Gp關于A={a1,a2,…,an}的非隸屬程度,其中0≤αpj≤1,,0≤βpj≤1,且0≤αpj+βpj≤1。那么敵方目標Gp關于A={a1,a2,…,an}的能力特征值用直覺模糊集<αpj,βpj>來表示,記為
rpj= {aj,<αpj,βpj>}(p=1,2,…,
m;j=1,2,…,n)
從而直覺模糊環境下G1,G2,…,Gm個敵方目標關于可以表示為矩陣形式:
R=(rpj)m×n=
假設能力特征aj(j=1,2,,…,n)相對于模糊概念“重要”的隸屬度為ρj,非隸屬度為ξj,其中0≤ρj≤1,0≤ξj≤1且0≤ρj+ξj≤1。那么能力特征aj的權重用直覺模糊集<ρj,ξj>來表示,記為ωj={aj,<ρj,ξj>}(j=1,2,…,n),從而直覺模糊環境下任務價值特征的權重可以表示為如下向量形式形式:
W= (ωj)1×n=
P(<ρ1,ξ1> <ρ2,ξ2> … <ρn,ξn>).
利用直覺模糊集規范化歐式距離公式和直覺模糊集算子,敵方目標Gp與能力需求模式P的非相似測度可以表示為

(1)
式中:
(2)
表示專家對于敵方目標關于Gp相對于A={a1,a2,…,an}能力估計的加權猶豫度;而
(3)
表示專家對于作戰任務P相對于A={a1,a2,…,an}能力估計的加權猶豫度。D越小,表示敵方目標Gp與能力需求模式P的匹配程度越高。
1.2 實例分析
假設我方的可選敵方目標有G1,G2,G3,G4,和G55個,分析5種敵方目標對于我方作戰任務的任務契合度指標Q。專家根據威脅等級、抗毀傷能力、成本價值、攻擊能力、協同能力、機動性能、偵察能力和支援保障能力[11]確定其作戰需求模式,其對應的權重直覺模糊集,任務需求直覺模糊集和5個敵方目標對應的能力指標值直覺模糊打分如表1所示,第1行表示8個指標權重,第2行表示對各權重的模糊隸屬度打分,第3-7行表示各目標對應8個指標的模糊隸屬度打分。
我們用s1,s2,s3,s4,s5,s6,s7,s8分別表示威脅等級、抗毀傷能力、成本價值、攻擊能力、協同能力、機動性能、偵察能力和支援保障能力8種任務價值需求的直覺模糊集,作戰需求模式集合S的數據如下:
權重向量為
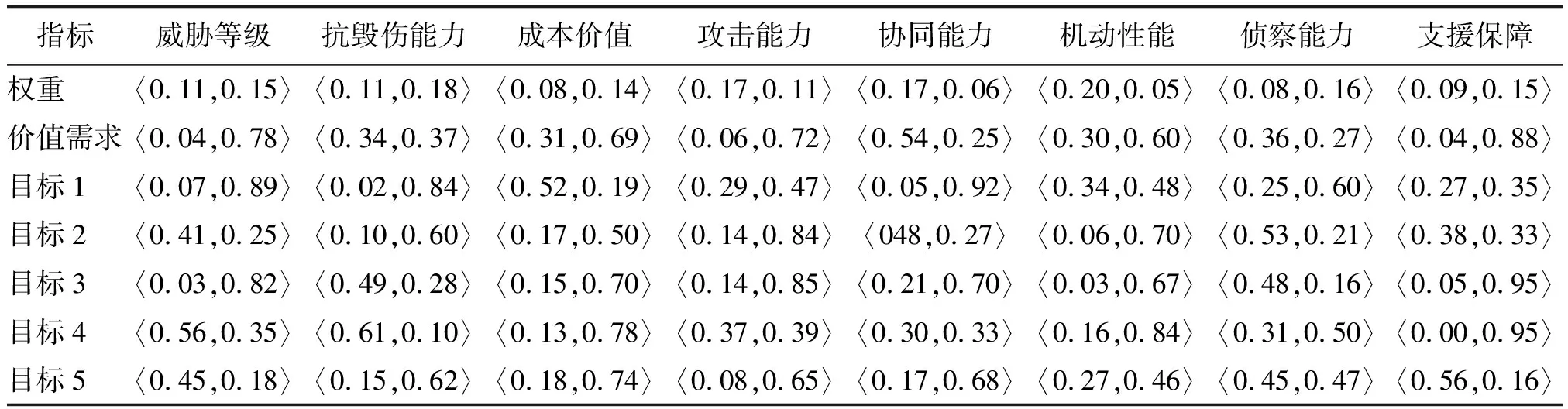
表1 指標權重、價值需求和目標模糊隸屬度打分結果表Table 1 Index weight, value need, and target fuzzy membership rating score results table
直覺模糊環境下5個敵方目標相對于8個任務價值需求的直覺模糊集指標值如下:
根據公式(1),(2),(3)計算任務價值敵方目標G1與作戰任務能力需求的非相似度
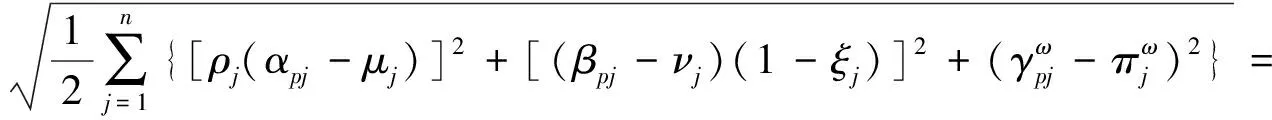
同理可計算出G2,G3,G4,G5與作戰任務能力需求的非相似度:
DG2=0.688 1,DG3=0.440 8,DG4=0.573 1,DG5=0.950 1.
因此可計算G1,G2,G3,G4,G5的任務契合度指標數據:
QG1=0.001 3,QG2=0.311 9,QG3=0.559 2,
QG4=0.426 9,QG5=0.094 9.
可以看出5個敵對目標的任務價值排序為3,4,2,5,1,目標5和目標1的任務契合度較低,在進行目標攻擊時優先選擇目標3,4,2。
2 密集火力攻擊WTA求解方法
本文的WTA問題是指求解對價值目標進行多次火力攻擊時艦艇平臺與目標的分配問題[12],包含每波次平臺目標分配情況和艦艇平臺多次目標攻擊的時間優化。任務價值編隊攻擊作戰時,通常會以最大規模進行協同攻擊[13],包括每波次導彈發射數量最大和縮短多波次打擊的時間間隔。當進行多次密集的火力攻擊時,如果認為每次火力攻擊不存在干擾,將會出現某艦艇敵方目標尚未完成上一波次火力打擊任務而又接到新的攔截任務的情況,從而導致任務失敗,所以對于連續多波次的火力攻擊,要合理考慮艦艇敵方目標資源占用情況。由于該問題求解規模較大,考慮的約束因素較多,所以本文采用改進的遺傳算法(GA)進行求解。GA是一種模仿自然演化規律的進化算法,通過把問題參數編碼產生一條染色體,通過選擇、交叉、變異等生成符合條件的染色體,該問題模型在決策變量為正整數,易于編碼,基于專家經驗的啟發式規則能夠極大地提高尋優速率,所以GA是解決該組合優化問題的有效方法[14-16]。
2.1 模型建立
數學模型及約束條件如下:
(1) 對已篩選出的敵方價值目標敵方目標進行編號,表示為P={p1,p2,…,pi…,pn},用pi表示第i個價值敵方目標。
(2) 對我方艦艇敵方目標進行編號,并表示為M={m1,m2,…,mj…,mm},用mj表示編號為j的艦艇敵方目標。不同艦艇敵方目標的反艦導彈攜載數量、發射準備時間和轉火調整時間不同。攜載反艦導彈數量約束體現在各艦艇敵方目標可參與的打擊波次數,不同敵方目標的發射準備時間和轉火調整時間不使用具體時間,以1~10的正整數表示,這是因為時間計算復雜,為簡化模型,只體現不同艦艇敵方目標所需時間的對比。
(3) 打擊波次序列集為OP={op1,op2,…,opj,…,opn},opj={opj1,opj2,…,opjk}表示敵方價值目標各波次打擊序列。
(4) 艦艇敵方目標目標匹配集合OPM={opi1,opi2,…,opik},opij={opij1,opij2,…,opijk},表示各波次中目標pi與各艦艇敵方目標的匹配序列集。
基于改進GA的算法流程為:建立符合條件的初始種群;計算染色體的適應度值,采用輪盤賭法擇優;通過整數交叉和整數變異得到新個體;不斷擇優直到達到設定遺傳代數,算法結束。算法流程如圖1所示。
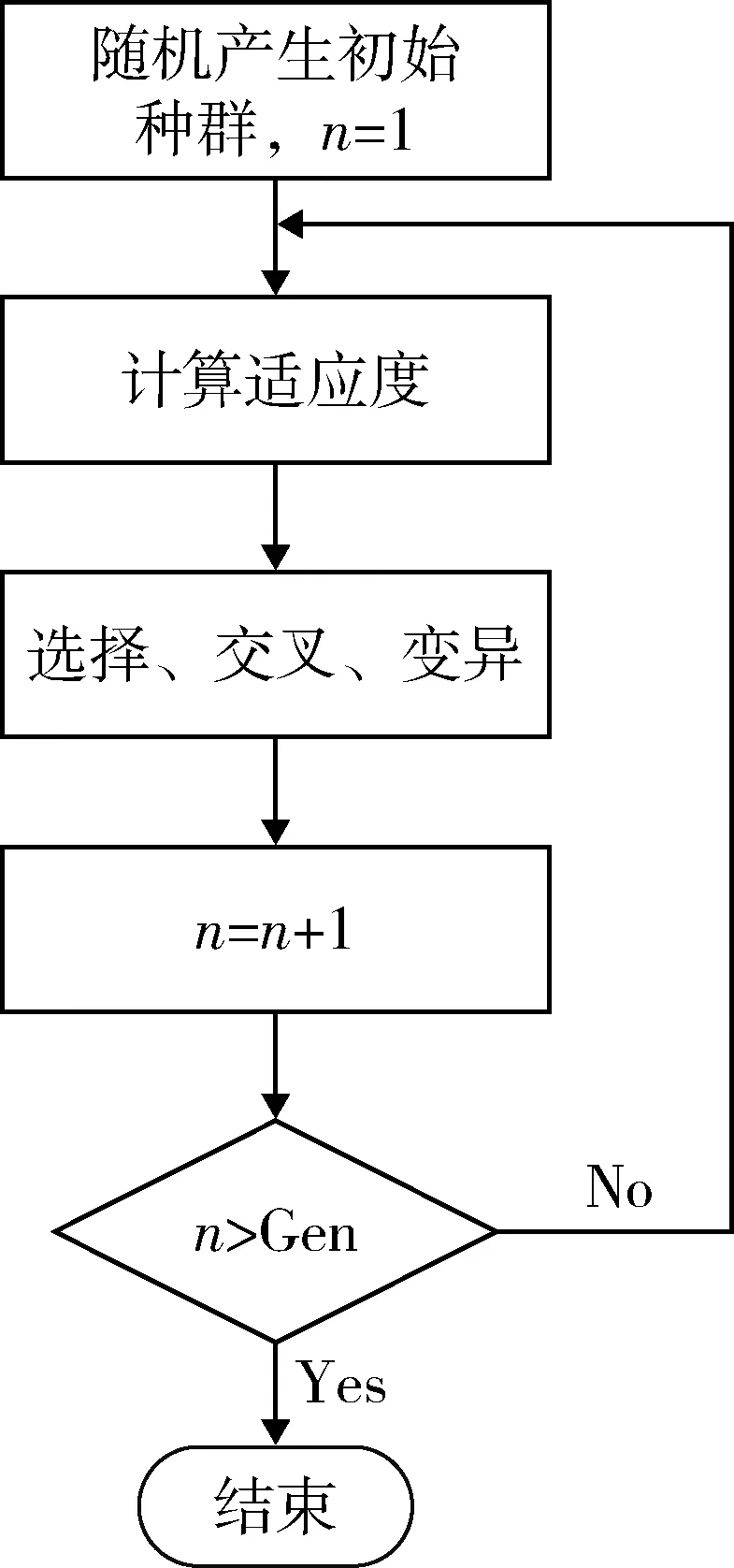
圖1 遺傳算法流程圖Fig.1 Genetic algorithm flow chart
2.2 算法實現
(1) 編碼
本文中要采用多層的十進制編碼方式來表達多層信息,即對待攻擊的n個價值目標進行m波次的攻擊,以長度為2nm的整數表示,前nm個整數表示對各價值目標打擊序列,后nm個整數表示各波次各價值目標匹配的艦艇敵方目標。
(2) 選擇適應度函數,本文中選擇完成全部波次打擊的總時間作為適應度函數,即
fitness(i)=time.
(3) 選擇操作
保證種群數量不變情況下,選擇適應度最好的個體到新種群中。通常采用輪盤法選擇,當待選擇個體總數為n時,個體i被選擇的概率一般表示為
(4)
產生一個(0,1)間的隨機數,按照個體編號順序依次對被選擇概率進行加總,如P1=0.15,P2=0.12,對于個體2而言,其對應的隨機數區間為[0.15,0.27],當隨機數為0.25時選擇個體2。
(4) 交叉操作
由于編碼的特殊性,交叉操作的個體為前nm位,并對交叉后缺失和多余的個體進行相應的目標和敵方目標調整。
(5) 變異操作
遺傳過程中會有基因發生突變的小概率事件,此時會產生新的個體。變異操作為選擇2個變異位置進行交換。
(6) 重復以上操作,選擇合適的遺傳代數,結束操作后選出最優排序。
2.3 算例求解
假設敵方待攻擊目標有4個,我方艦艇平臺構成為2艘護衛艦和1艘驅逐艦,記為a,b和c,分別可進行的攻擊波次數為2,2,4;考慮轉火攻擊時增加的發射準備延遲,將轉火后再攻擊記為一次新的攻擊方式,那么一共有包括平臺1的2次攻擊,平臺2的2次攻擊,平臺3的4次攻擊的8種攻擊方式,編號為1,2,3,4,5,6,7,8擬進行3波次密集火力攻擊。目標波次與攻擊方式匹配如表2,對應的耗用時間如表3。
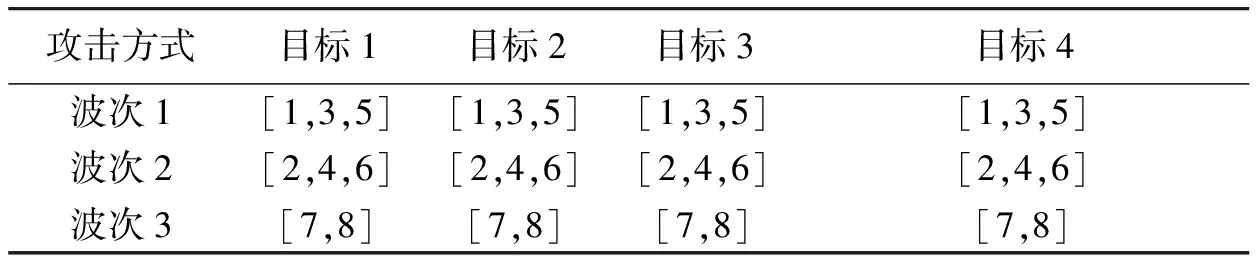
表2 目標波次攻擊方式匹配表Table 2 Target, attack wave, and attack mode match table

表3 目標波次攻擊方式耗用時間表Table 3 Target, attack wave and attack duration table min
算法設定種群數目為40,最大迭代次數為50,交叉概率0.8,變異概率0.6。結果顯示為,所需最短時間為16,一種攻擊方案如圖2所示,用3位數序列表示目標和對應波次,如202所在位置表示目標2第2波次攻擊分配給艦艇平臺3的第2次轉火攻擊。
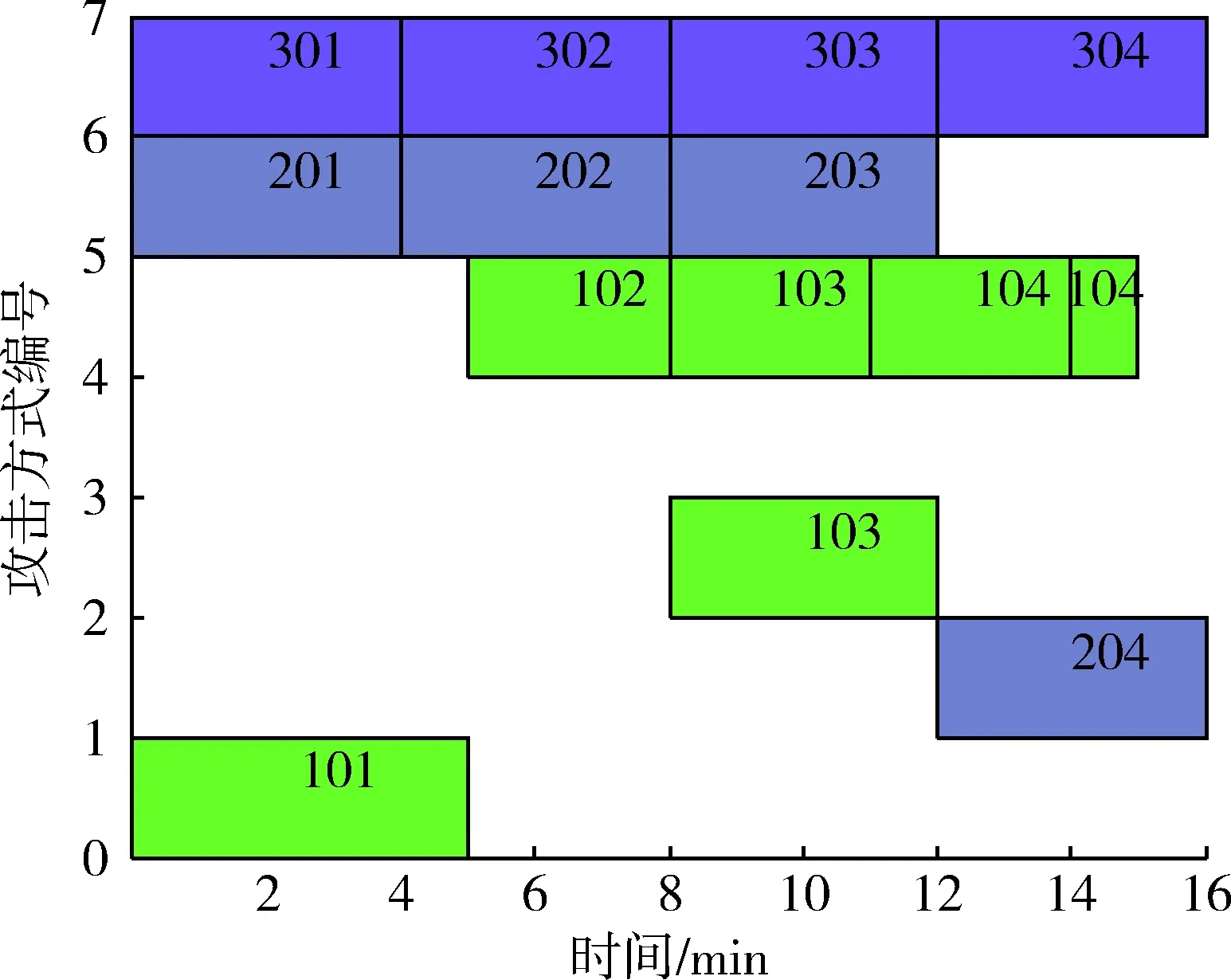
圖2 目標打擊方式分配結果圖Fig.2 Target strike distribution results graph
種群均值和最優個體的適應度變化情況如圖3所示,可以看出,由于數據規模小,在第7代左右就可以求出最優個體,對于更大規模和層次的WTA問題可以通過增加遺傳代數進行求解。
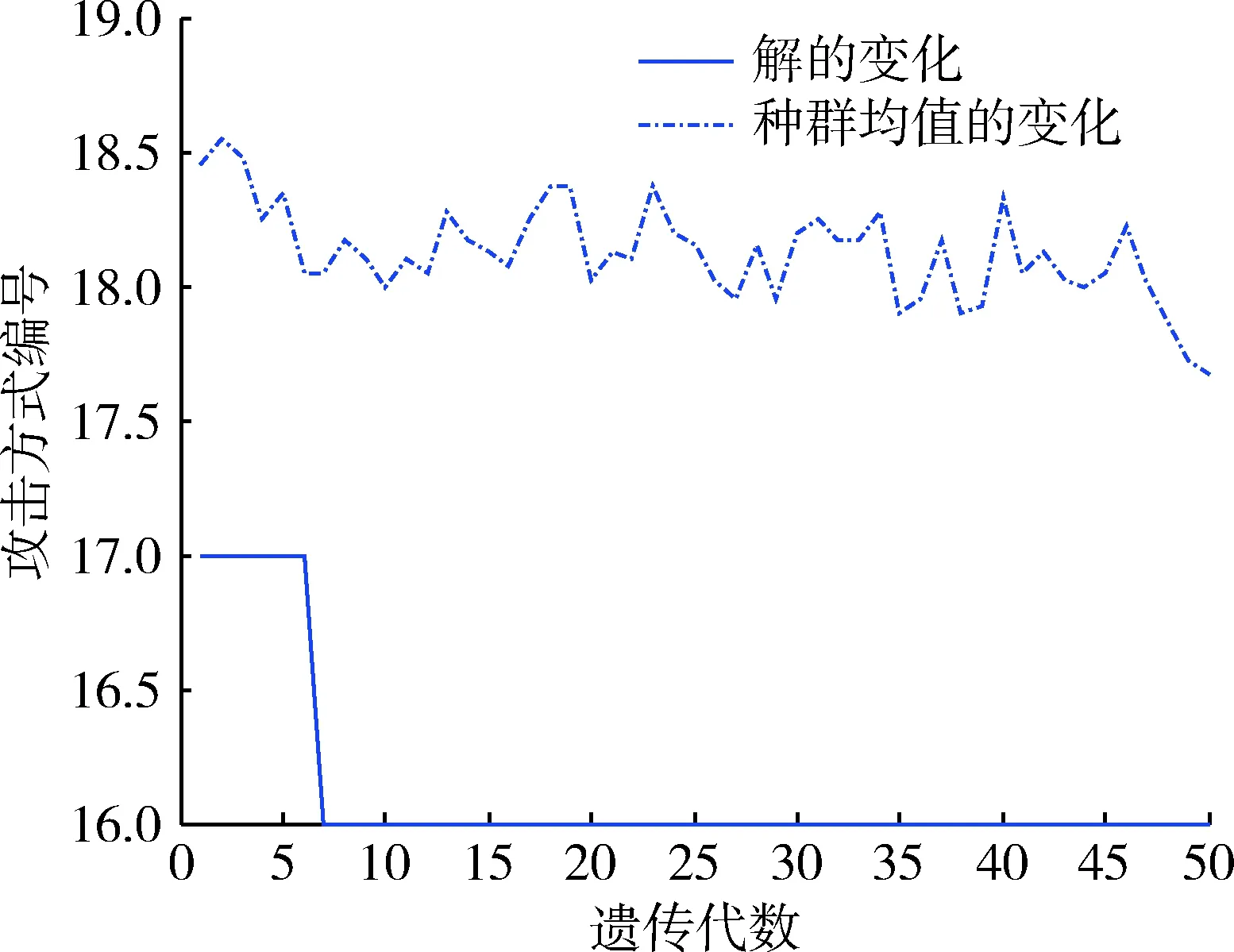
圖3 解和種群均值變化表Fig.3 Solution and mean value ofpopulation changes table
3 結束語
針對多目標攻擊場景下火力打擊問題,提出了一種基于模糊隸屬集理論的目標任務契合度計算方法,建立了多波次火力攻擊平臺目標分配模型,并通過算例求解進行了驗證,對艦艇編隊密集火力打擊下的作戰決策有一定參考價值。

