基于線性非線性回歸分析的防空導彈費用建模*

趙曰強，安實，麥強，于道林，張耀東

(1.哈爾濱工業大學 管理學院，黑龍江 哈爾濱 150001；2.中國航天科工防御技術研究院，北京 100854；3.北京電子工程總體研究所，北京 100854)

0 引言

研究防空導彈武器系統費用時，導彈的生產費用單價最受關注。這是因為在武器系統中導彈的技術性能指標可比性強，而地面系統由于使用要求不同，配置繁簡差別顯著，費用的統計測算離散很大；從整個壽命周期費用來看，生產費用最穩定，研制階段由于受到技術基礎、研制周期、試驗鑒定次數的影響費用離散很大；另外，現實中很多防空導彈武器系統的研制生產，一般將導彈和雷達制導等地面系統由不同的承包商分開承擔，導彈相對獨立性強。綜上所述，從導彈的生產費用單價入手易于得到可靠的費用模型。

1 費用變量的分析與選擇

費用變量是指影響導彈費用的敏感量[1]。防空導彈武器系統性能指標較多，各指標對費用都有一定的影響，相互間還存在著復雜的關聯性[2]。下面對主要技術性能參數進行相關性分析與選擇。

首先分析導彈殺傷空域對費用的影響。一般來說在有效載荷(一般指戰斗部)給定的情況下，射程增大往往造成發射質量增大，進而引起費用的增加。另外，在射程一定的情況下，提高推進劑的性能雖然可以降低導彈發射質量，但推進劑的費用必定隨著增大。提高制導精度可以降低有效載荷，進而大幅降低發射質量，但制導系統的成本會大幅度提升，這在一定程度上會抵消導彈發射質量降低帶來的好處。可以看出，在一定制導體制下，射程是影響費用的主要因素。

然后分析導彈質量對費用的影響。發射質量決定了導彈的大小，從而也決定了所需的動力消耗。發射質量越大，費用越大；戰斗部質量決定了導彈的殺傷威力，在炸藥類型相同的情況下，威力增大，戰斗部質量增大，對制導精度的要求降低。可以看出，戰斗部質量的變化將從導彈質量和制導精度2個方面影響導彈的費用，其對經費的影響不是單一的增減關系。

此外分析導彈飛行速度對費用的影響。導彈飛行速度增大，可縮短射擊周期，提高火力密度，增大有效發射區和殺傷區。同時，導彈飛行速度的提高對導彈控制能力、結構、防熱水平等都提出了更高的要求，進而導致導彈費用的增加。

導彈殺傷概率直接取決于導彈的制導精度、引戰配合和殺傷威力。其中，制導精度對導彈殺傷概率的影響至關重要。

導彈的可靠性和維修性相關費用可以按導彈武器系統總費用的一定比例來概算[3]。

通過以上分析，結合對導彈武器系統費用敏感的幾個主要參數(殺傷空域、導彈質量、飛行速度、戰斗部質量、制導精度、目標通道等)，選取以下參數作為研究影響導彈單價的自變量：最大射程、發射質量、最大飛行速度、戰斗部質量以及制導誤差。

在較早的模型中，自變量多選用發射質量、發動機裝藥、戰斗部質量、最大射程等組合[4-5]。這是由于20世紀80年代以前的防空導彈多是第1代、第2代的產品，技術水平接近，例如：均采用指令制導、脈沖多普勒雷達。后來隨著技術的發展，出現了相控陣雷達，防空導彈可以打擊多目標。于是出現了以最大射程和多目標數作為自變量的組合。但是現今的導彈制導控制技術得到了大幅度的提升，TVM制導、主動雷達末制導、光學制導和使用直接力控制使得制導精度越來越高，甚至具備了直接碰撞的能力。所以傳統的變量參數(如戰斗部質量mz)已經難以包含影響導彈費用的全部主要因素；因此，本文引入了新的變量制導誤差ρ。另外，多目標能力在全系統費用的估算中將是關鍵因素之一，系統費用建模時要予以關注[6]。

2 導彈生產費用單價的線性建模

關于防空導彈的生產費用單價和性能參數，數據來源較多，數據的可信度較高，因此可采用參數法。具體而言，首先從已經選出的有代表性的性能參數中確定對導彈費用敏感的自變量，例如：最大射程R，發射質量m，導彈最大飛行速度vm以及導彈制導誤差ρ。然后，收集整理類似其他項目的歷史數據。最后利用統計回歸分析技術建立起費用與自變量間的關系。

假定導彈生產費用單價y(Cmp)與各參數x1～4(R，m，vm，ρ)之間具有如下的線性函數關系：

y=b0+b1x1+b2x2+b3x3+b4x4+e，

(1)

式中：e為服從獨立正態的隨機變量。

運用多元線性回歸分析來確定式(1)中的待定參數b0，b1，b2，b3，b4。

可見對x1～4(R，m，vm，ρ)的n組不同取值(R1，m0，vm1，ρ1)，(R2，m2，vm2，ρ2)，…，(Rn，mn，vmn，ρn)；有對應的y(Cmp)的值Cmp1，Cmp2，…，Cmpn。

(2)

式中：X為自變量矩陣；Y為因變量；B為回歸系數；E為隨機誤差，由式(1)得

Y=XB+BE，

(3)

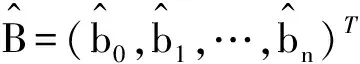
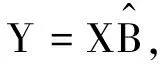
(4)

變換得

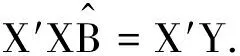
(5)

假定(X′X)的逆矩陣(X′X)-1存在，則得到式(5)回歸問題的最小二乘解為

(6)

2.1 大中型導彈生產費用單價線性模型的建立

建模用到的樣本數據真實有效性是取得良好統計結果的關鍵，參照文獻[7-11]等，查找分析幾個國內外最新防空導彈型號的性能參數和費用數據，并參照美國國防部公布的陸軍緊縮指數，對于不同時間價格水平進行比較，整理列于表1中。

由表1中導彈主要性能技術參數作為自變量x1～4(R，m，vm，ρ)，導彈生產費用單價y(Cmp)作為因變量，進行多元線性回歸分析，運用Matlab運算得：

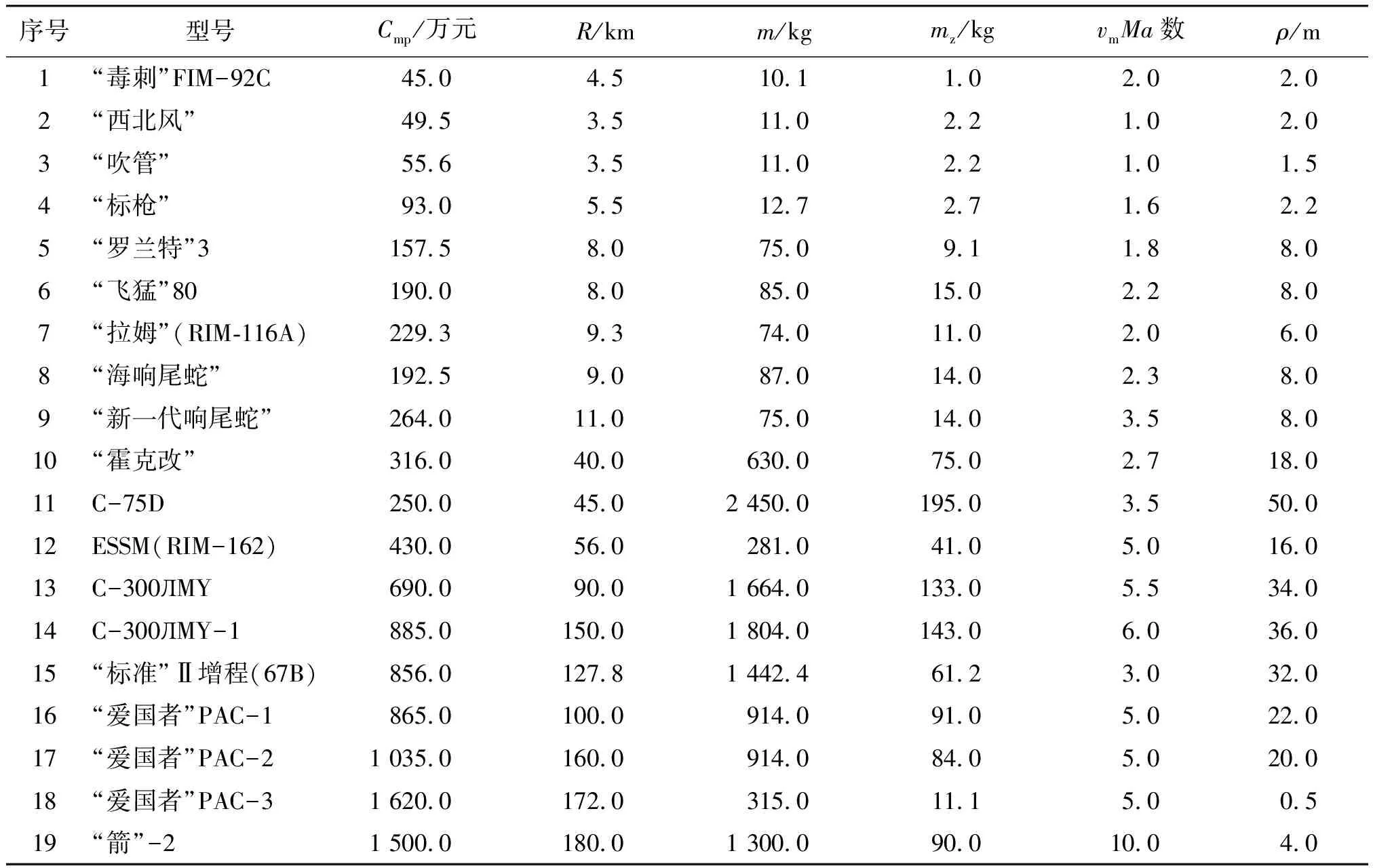
表1 幾種防空導彈費用數據

注：Cmp為折算的2010年數據，單位人民幣萬元

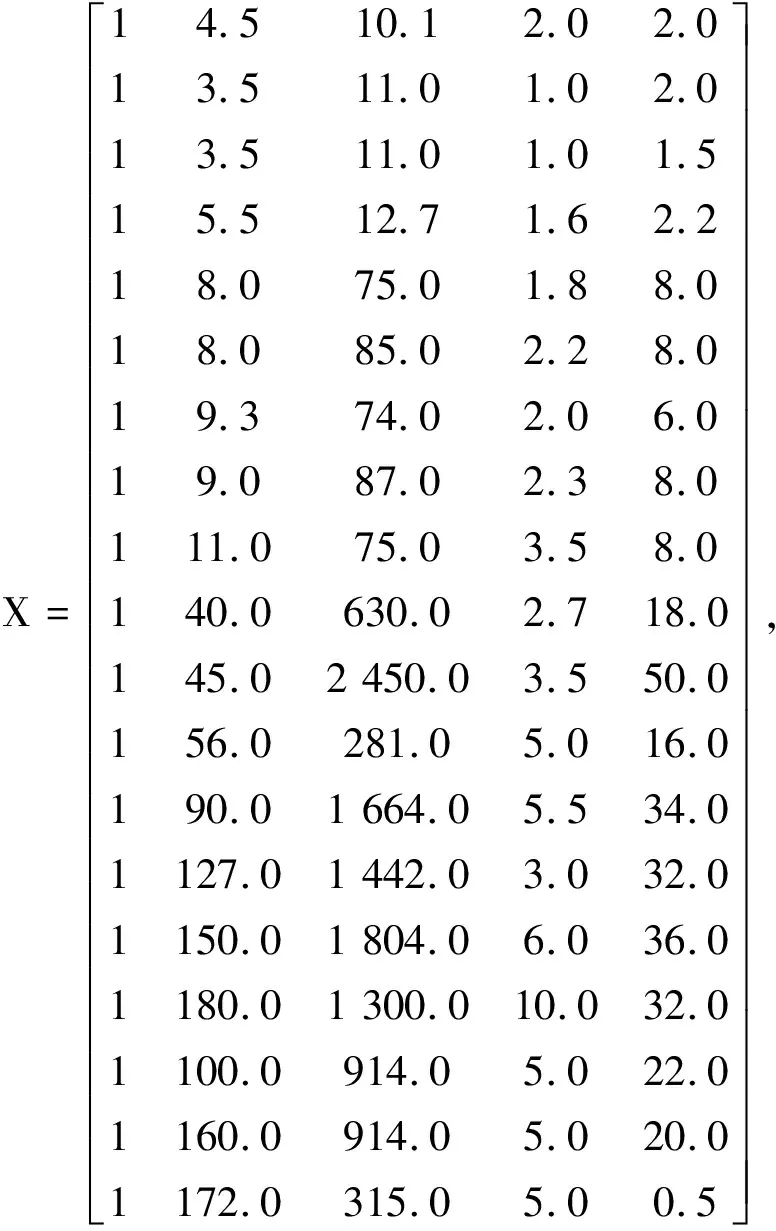
Y= (45.0，49.5，55.6，930.0，157.5，190.0，229.3，

192.5，264.0，316.0，250.0，430.0，690.0，885.0，

856.0，865.0，1 035.0，1 620.0，1 500.0)T.

(7)

將式(7)代入式(2)，得

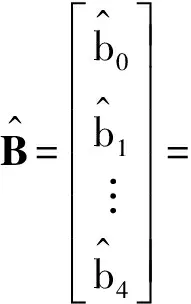
(8)

代入式(1)，則得回歸費用模型：

y= 61.940 2+6.362 1x1-0.126 8x2+

52.780 6x3-13.426 3x4.

(9)

首先利用表1樣本值和計算值對模型進行驗證，由式(9)得出計算值和歷史數據值進行比較可以看出，小型導彈的費用估算偏差較大，最大到了279.02%，該模型已經不能適用；該模型對大中型導彈的適用性略好。

這里，解決模型對小型導彈和中大型導彈擬合結果偏離的問題，美國陸軍導彈系統全壽命費用模型中對于研制費用提供了3個CER解析式，其中第一個只能適用于便攜導彈的費用估計[12-13]。這也得到一些提示，可以對小型和大中型導彈的費用估計進行分段處理。通過對導彈數據的分析，選用導彈發射質量30 kg作為分段點。

先來看發射質量大于30 kg的導彈費用的估計。將表1中序號5～19導彈發射質量大于30 kg的導彈主要性能技術參數作為自變量，進行多元線性回歸，則得大中型導彈的回歸費用模型：

y= 192.866 9+5.483 0x1+0.369 2x2+

61.753 7x3-27.243 9x4，m>30 kg.

(10)

同樣先利用樣本值和計算值對模型進行驗證，由式(10)得出計算值，和樣本值對比看出，對于大中型導彈通過多元線性回歸得到的導彈生產單價的費用估算模型并由此而得到的計算值和歷史數據(樣本值)吻合的較好，有一半的數據偏差在5%以內，最大的偏差僅為21%。

我們進一步對模型的多元回歸進行方差分析，分析結果見表2。

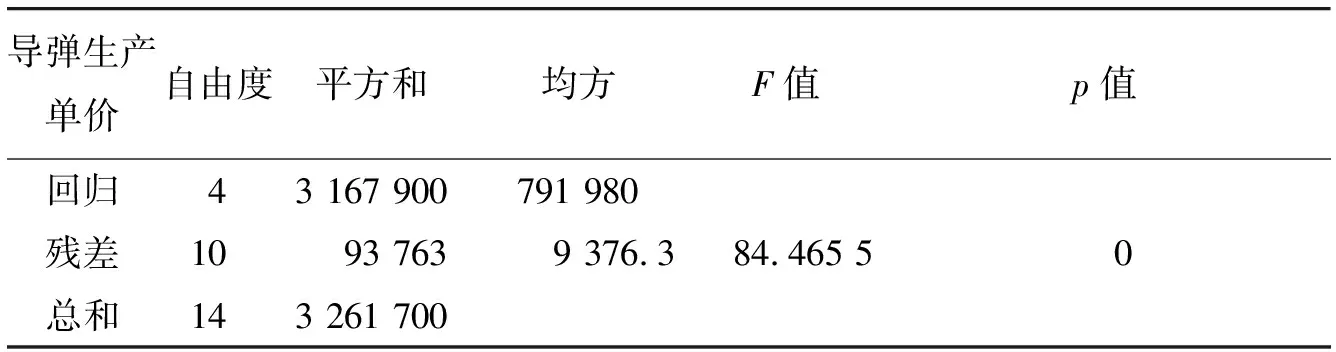
表2 多元線性回歸的方差分析Table 2 Variance analysis of multivariatelinear regression

相關系數值為

R2=3 167 900/3 261 700=0.971 3.

(11)

調整相關系數值為

Ra2=1-9 376.3/(3 261 700/14)=0.959 8.

(12)

可見有超過95%的費用發生是由選定的4個變量(R，m，vm，ρ)決定的。

Ra2和R2數值差別不大，沒有出現Ra2數值遠小于R2的情況，說明參數選擇數量合理。

查F分布表可得F4，10(0.01)=5.99<84.465 5(統計量F的值)，同時檢驗的概率P<0.01，所以，假設H0：b1=b2=b3=b4=0不成立，回歸方程通過了顯著性檢驗，即認為所得的線性回歸方程有意義。

2.2 小型導彈生產費用單價線性模型的建立

現在將幾種發射質量小于30 kg的導彈生產單價和主要性能技術參數整理見表3。

從對表2中的數據分析可以看出，小型便攜導彈制導體制相近，制導精度相當，導彈生產單價和作戰空域、速度以及戰斗部質量關聯不大，而和導彈的發射質量關聯顯著，通過各種參數組合為自變量的回歸及方差分析也可以說明這一點。

將表3中導彈發射質量作為自變量，導彈生產單價作為因變量，進行線性回歸，得小型導彈的回歸費用模型：

y=-7.489 0+5.564 7x2，m≤30 kg.

(13)

同樣先利用樣本值和計算值對模型進行驗證，由式(13)得出計算值，和樣本值對比看出，由導彈生產單價的費用估算模型得到的計算值和歷史數據(樣本值)最大偏離13%，偏差不大。

進一步對回歸模型進行方差分析，見表4。

對α=0.05，查F分布表可得F1，6(0.05)=5.99。

因為F>F1，6(α)，同時，p=0.026 2<0.05，線性回歸方程反映了導彈生產單價和導彈發射質量的相關關系。

2.3 導彈生產費用單價多元線性回歸模型

根據上面的計算和仿真，以導彈發射質量30 kg為分界線建立分段函數，建立起導彈的生產費用單價y(Cmp)的線性模型。

(14)

式中：y(Cmp)為導彈的生產費用單價，萬元(人民幣)；x1(R)為導彈的發射質量，kg；x2(m)為導彈的最大射程，km；x3(vm)為導彈飛行的最高Ma；x4(ρ)為導彈制導誤差，m。

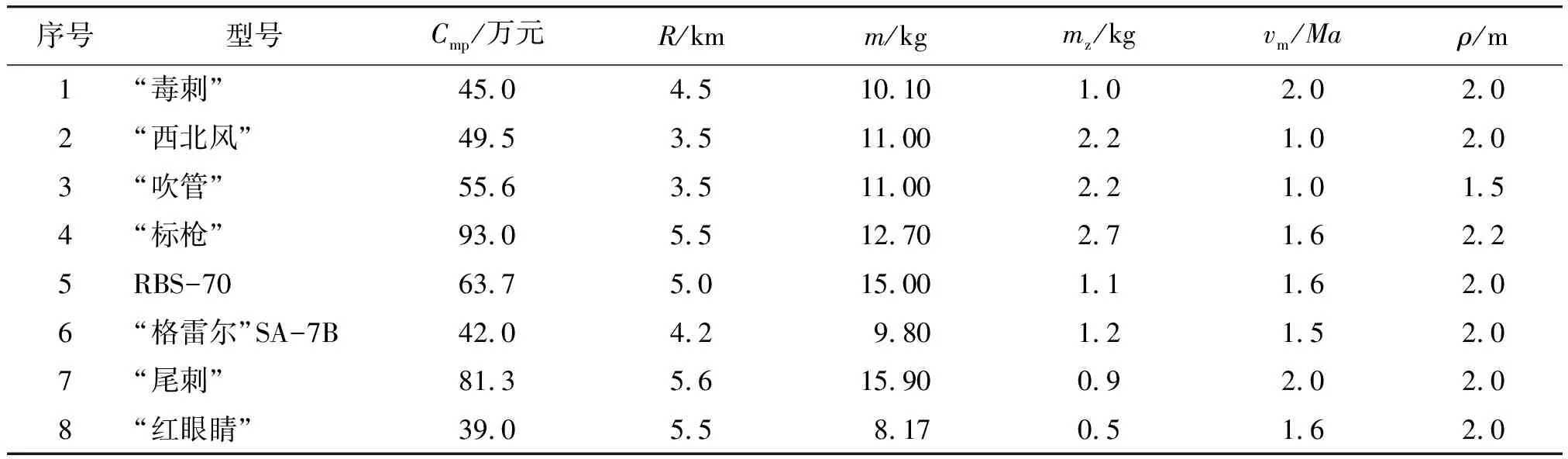
表3 幾種小型防空導彈費用數據Table 3 Cost data of several small air defense missiles

注：表中Cmp為折算的2010年數據，單位人民幣萬元。

表4 小型導彈多元線性回歸的方差分析Table 4 Variance analysis of multivariate linearregression for small missile

3 導彈生產費用單價的非線性建模

上節建立起了導彈的生產費用單價與特性參數之間的線性函數關系。采用了對小型和大中型導彈的費用估計進行分段處理，取得了理想的結果。下面進一步開展非線性分析，建立非線性回歸模型，來探求比較形成最佳的解決方案[14]。

基本原理是非線性回歸最小二乘擬合[15]。利用Matlab非線性曲線擬合命令nlinfit函數，進行非線性函數的系數用最小二乘法估計，該函數使用高斯—牛頓算法，調用格式為

beta=nlinfit(X,y,@myfun,beta0).

(15)

式中：y為因變量矢量；X為自變量組成的矩陣；beta0為包含系數初始值的矢量；@myfun參數為一函數，具有以下的形式

yhat=myfun(beta,X)，

(16)

式中：beta為系數矢量；X為自變量矩陣；@myfun為參數返回一個擬合y值的yhat矢量。

3.1 建立二次函數模型

設定y(Cmp)與各參數x1～5(R，m，mz，vm，ρ)之間具有如下的函數關系：

y= beta1x1+beta2x2+beta3x3+beta4x4+beta5x5+

beta6x12+beta7x1x2+beta8x1x3+beta9x1x4+

beta10x1x5+beta11x22+beta12x2x3+beta13x2x4+

beta14x2x5+beta15x32+beta16x3x4+beta17x3x5+

beta18x42+beta19x4x5+beta20x52.

(17)

這里構建的是含有平方項和交互項的二次函數表達式。

調用Matlab中nlinfit函數進行估算，得到beta為系數矢量，beta(20)為極小值，且超出置信區間略去，即得到最終的多元二次非線性回歸的解析式：

y= -221.64x1-49.448x2+609.5x3+168.38x4-

144.07x5-0.1807 5x12-0.249 01x1x2+

0.816 3x1x3+72.346x1x4+3.574 5x1x5-

0.035 167x22-0.269 65x2x3+11.512x2x4+

4.598 9x2x5+10.215x32-192.42x3x4-

60.829x3x5-105.38x42+202.59x4x5，

(18)

式中：y(Cmp)為導彈的生產費用單價，萬元(人民幣)；x1(R)為導彈的發射質量，kg；x2(m)為導彈的最大射程，km；x3(mz)為戰斗部的質量，kg；x4(vm)為導彈飛行的最高Ma；x5(ρ)為導彈制導誤差，m。

對該模型進行回歸檢驗，由命令函數[b,bint,r,rint,stats]=regress(y_result,x)，得檢驗回歸模型的統計量：

stats=(0.959 47，86.075，1.074 4e-9，12 430).

(19)

可見，相關系數平方值R2=0.9594 7說明回歸方程顯著模型擬合程度較高，F=86.075不超臨界，顯著性概率P=1.074 4e-9<0.05拒零假設，模型有意義，均方根誤差RMSE=12 430。

采用式(18)，利用表1中的導彈費用數據擬合結果為

Y_result= (45，49.5，55.6，93，157.5，190，229.3，

192.5，264，316，250，430，690，885，

856，865，1 035，1 620，1 500).

(20)

將擬合值與樣本值進行對比見圖1。

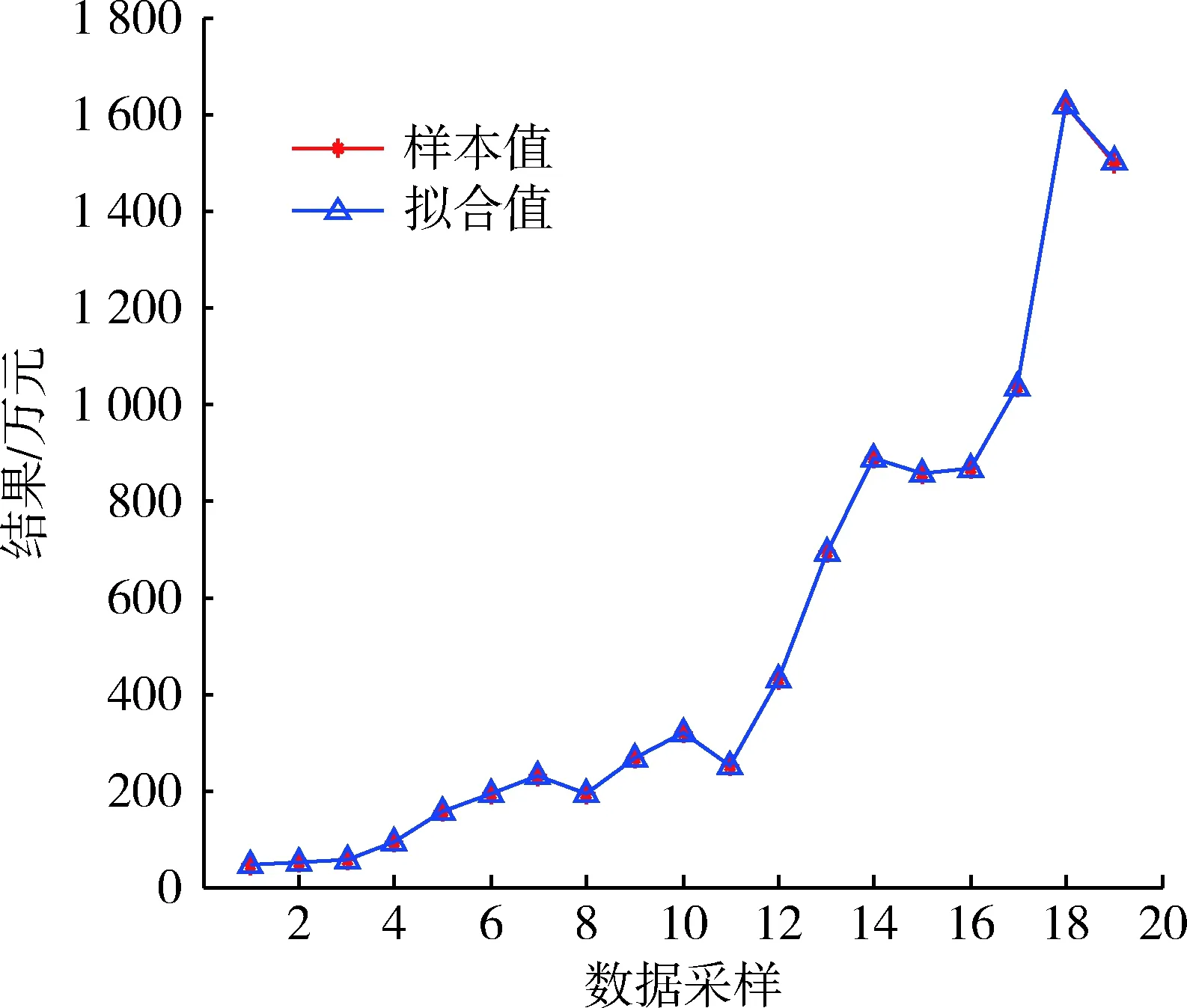
圖1 二次函數模型擬合值與樣本值對比圖Fig.1 Contrast diagram of fitting value and samplevalue of quadratic function model

本模型擬合精度高，用一個解析式較一致地表達了因變量和各參數的關系，而不需要采用分段表示。相對線性回歸模型，該模型具有更高的計算復雜性，適合使用計算機進行計算。

3.2 建立非線性函數模型

為了進一步簡化允許特定一點出現較大偏差(可視孤立樣本予以剔除)的條件下的擬合的函數。先看下每個參數對性能的影響，確定交互項和單一項，然后遍歷所有指數的可能，獲得和原始數據的最小誤差。建立生產費用單價的模型：

y= -71.589+8.692x1-727.39x4- 9.710 4x10.5x30.5+749.1x20.05x40.9，

(21)

式中：y(Cmp)為導彈的生產費用單價，萬元(人民幣)；x1(R)為導彈的發射質量，kg；x2(m)為導彈的最大射程，km；x3(mz)為戰斗部的質量，kg；x4(vm)為導彈飛行的最高Ma。

采用上式，利用表1中的導彈費用數據擬合結果為

Y_result= (61.364，49.017，49.017，73.463，

183.54，193.23，189.77，206.49，228.13，

308.03，281.18，540.08，681.78，911.92，

895 718.29，1 040.4，1 613.6，1 499.2).

(22)

將擬合值與樣本值進行對比如圖2所示。

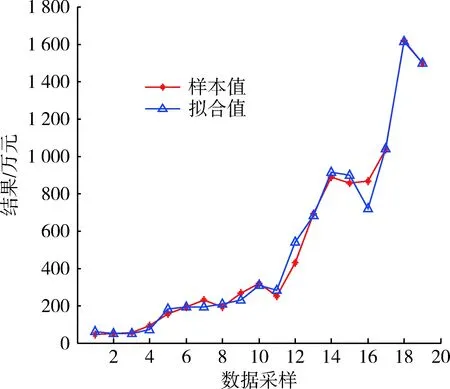
圖2 非線性模型擬合值與樣本值對比圖Fig.2 Contrast diagram of fitting value andsample value of nonlinear model

對該模型進行回歸檢驗，得檢驗回歸模型的統計量

stats=(0.968 53，110.25，2.032 3e-10，9 557.2).

(23)

可見，相關系數平方值R2=0.968 5說明方程回歸顯著，顯著性概率P=2.032 3 e-10<0.05存在非零系數，說明擬合模型有效。

該模型式(21)和原數據總的誤差為540，平均每個點的誤差為28.4，最大點的誤差為150.5。

本模型相對二次函數模型式(18)大為簡化，檢驗有效，但是從圖2可知，整體擬合較好，個別點有一定的偏差(17%以內)。

4 結束語

采用線性回歸的方法建立導彈生產費用模型式(14)，由于選取的參數典型且與費用相關大，建立的模型相對簡單且精度高，易于計算，且物理意義明確，不足之處是要根據導彈的總質量大小分兩段進行擬合。非線性回歸二次函數建模、非線性建模都取得了很好的結果，避免了線性回歸模型分段的不足；但計算略復雜，適合計算機運算。二次函數模型式(18)精度除質量小、近程的個別裝備，整體精度較高，但結構復雜，幾乎包含了各參數的平方項和交互項；非線性模型式(21)結構簡單，精度較好，能用一個式子簡明準確地表達了所有防空導彈的生產費用單價。本文建模選取的費用變量雖然相關性較高，但在應用中還應根據工程實際，考慮其他費用變量的作用。