一種非線性模型下的復合材料螺栓連接失效分析

李沛城，常楠，趙美英，黃河源

(1.西北工業大學 航空學院，西安 710072) (2.中國航空工業集團有限公司 成都飛機設計研究所，成都 610041)

0 引 言

考慮到減輕結構重量，提高經濟性等因素，現代飛機存在大量由聚合物基纖維增強復合材料制造的結構件，其中螺栓連接結構是一種較為常見的形式。目前，復合材料螺栓連接結構的主要研究方法可分為三類：試驗法[1-4]、解析法[5-11]和有限元法[12-15]。其中，試驗法的經濟及時間成本較高；解析法則通過建立合理的連接剛度或連接柔度來計算螺栓的載荷分配，具有形式簡單且計算高效的特點，適用于大規模螺栓連接結構的極限強度預測和釘載分配計算，但難以對結構局部的損傷發展規律進行分析；相較而言，有限元法通過建立適當的材料本構，可以在合理預測復合材料螺栓連接結構強度的同時，幫助研究者理解其復雜的力學響應特性。

復合材料螺栓連接拉伸失效問題具有明顯的三維特征[16]，因而相對簡單的二維失效準則在對此類結構進行有限元分析時效果不太理想。早期的復合材料螺栓連接三維有限元模型以應力分析為主，之后經過不斷探索，三維有限元模型已發展到能夠采用各種不同的損傷本構關系對復合材料連接結構進行損傷失效分析的程度。M.A.McCarthy等[12-13]通過三維恒應力退化模型研究了復合材料多釘連接結構的釘載分配比例以及釘孔間隙對其力學響應特性的影響；C.Huhne等[14]基于三維Hashin失效準則，分別采用恒應力退化和連續退化模型對復合材料單釘單搭接結構進行了漸進損傷失效分析，表明采用恒應力退化模型所得結果偏保守，而連續退化模型的結果則與試驗結果更為接近；A.Olmedo等[15]結合擴展的Chang-Chang及Chang-Lessard失效準則，考慮了層合板的三維應力場分布、面外失效模式以及非線性剪切應力-應變關系，在ABAQUS/Standard求解器中采用USDFLD漸進損傷退化子程序對復合材料螺栓連接結構進行失效分析，并在此基礎上針對摩擦系數和擰緊力矩進行了參數影響分析。

材料的微觀損傷累積是復合材料宏觀上呈現非線性響應的重要因素。因此，在對復合材料層合板相關結構進行三維失效分析時，需建立適當的同時包含損傷判據與材料退化方法的本構模型，從而獲得可靠的應力-應變關系。本文采用的復合材料非線性損傷本構模型通過綜合Hashin失效準則、能量耗散率方法和Puck失效準則來計算單元失效前的面內與面外損傷，同時結合材料非線性連續退化方法對單元發生損傷后的力學性能進行計算；將準各向同性ZT7H/5429復合材料開孔板準靜態拉伸數值仿真與試驗結果進行對比，驗證上述方法建立的非線性損傷模型的有效性，在此基礎上對復合材料單釘雙搭接螺栓連接結構開展強度預測和損傷失效分析。

1 復合材料損傷模型

1.1 損傷本構

復合材料內部微觀裂紋的不斷累積是其面內宏觀非線性響應的重要因素。在研究含損復合材料時，應力應變關系為損傷變量d的函數。

(1)

式中：σ(d)為含損有效應力；C(d)為材料含損剛度矩陣；G(d)為含損Gibbs自由能密度。

1.2 損傷起始及演化

1.2.1 基于Hashin準則的面內纖維損傷

采用應力表達的材料失效判據是一種常見的形式[17]。但當復合材料纖維發生損傷時，對應位置的單元應力存在明顯波動，而應變在此過程中的變化則相對平緩。因此，作為本文纖維損傷判據的三維Hashin失效準則采用如式(2)所示的基于應變的表達形式。

(2)

式中：df為材料纖維方向的失效參數。

當復合材料在外載作用下發生損傷時，其內部纖維損傷狀態變量d11遵循指數型損傷演化規律對材料進行非線性漸進退化[18-21]。

(3)

式中：LC為單元特征長度，引入該參數能將斷裂能平均地分布到各個單元體內，是降低材料損傷退化過程中單元尺寸依賴性的一種有效手段。

1.2.2 基于能量耗散率方法的面內基體損傷

面內基體損傷包括基體拉伸損傷d22和基纖剪切損傷d12，可通過能量耗散率推導得出，其中，算子=max(x,0)。

(4)

(5)

定義損傷驅動函數如式(6)～式(7)所示，通過計算獲得損傷變量d22和d12的值。

(6)

(7)

式中：a為基體拉伸損傷與纖維/基體剪切損傷耦合系數；Y12(N)與Y22(N)定義為當前載荷步N期間內剪切損傷與拉伸損傷的驅動量最大值。

(8)

(9)

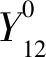
1.2.3 基于Hashin準則的面外損傷

對于復合材料基體面外損傷，基于應變的三維Hashin失效準則如式(10)所示。而后可通過式(11)與式(12)計算相應的材料內部損傷變量d33、d13和d23[18-21]。

(10)

(11)

(12)

(13)

1.2.4 基于Puck準則的基體損傷

基體材料常見的失效模式有三種，包括拉伸失效、壓縮失效和沿某斜面的斷裂失效。在三維應力狀態下，基體沿厚度方向上的應力變化非常復雜，其破壞常呈現出一定的斷裂角度。復合材料螺栓連接結構孔邊單元沿厚度方向上的應力梯度較大，此時三維Puck失效準則可作為復合材料失效判據的重要補充。

對于復合材料單向帶，其基體斷裂面的三維應力狀態如圖1所示，σn為斷裂面法向牽引力，σL為斷裂面沿纖維縱向牽引力，σT為斷裂面沿纖維橫向牽引力。

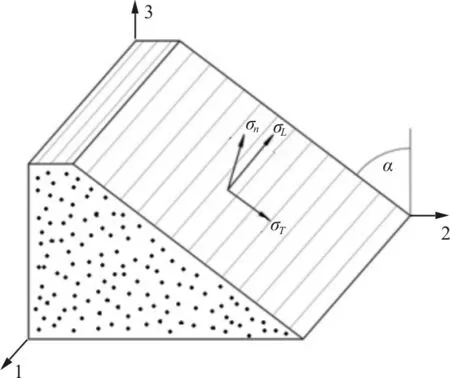
圖1 斷裂面應力分量

在斷裂面狀態下的基體損傷因子為

(14)

復合材料層合板中單層由于位置不同會存在不同的力學特性，即就位效應。本文研究的ZT7H/5429復合材料單層厚度為0.125 mm，屬于薄就位層，故式(14)中

(15)

式中：YT為橫向拉伸就位強度；SL、ST分別為縱向、橫向就位剪切強度；μL、μT分別為沿纖維縱向和橫向的摩擦系數。

Puck通過研究發現，基體典型斷裂角為53°±2°(本文取值為53°)[22-23]。

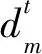
考慮到基體材料發生損傷后，其力學性能通常是逐漸降低的，因此本文針對基體材料采用的是一種非線性漸進損傷退化模型，其表達式為[24]：

dm=maxn≤N

(16)

其中，

(17)

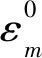
另外，式(16)中的dmax為損傷變量最大值，其理論值小于1，實際計算時可取一個接近于1的數值，本文取0.98。

1.2.5 斷裂模式與基體損傷變量的確定

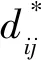
表1 斷裂角、斷裂模式與基體損傷變量的關系

通過Puck失效準則，根據計算所確定的基體斷裂角，參照表1可以判斷出對應的基體斷裂模式，從而確定相應的基體損傷變量。

2 模型驗證

基于上述復合材料三維非線性本構建立開孔層合板有限元模型，并結合相應試驗對其進行有效性驗證。

2.1 開孔層合板試驗概況

開孔層合板準靜態拉伸試驗件所用復合材料為ZT7H/5429，鋪層順序為[45/0/-45/90]2s，其幾何參數如圖2所示，材料力學性能參數如表2所示[25]。試驗在室溫條件下進行，參考ASTM-D5766標準，加載設備為CSS-88100電子萬能試驗機，通過位移控制加載，加載速率為2 mm/min；應變片采用BQ120-3AA，膠粘劑選用B-711，應變采集系統為東海DH3820型多通道應變自動采集處理系統。

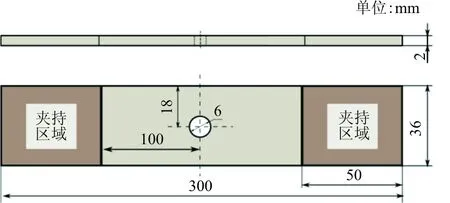
圖2 開孔板尺寸示意圖

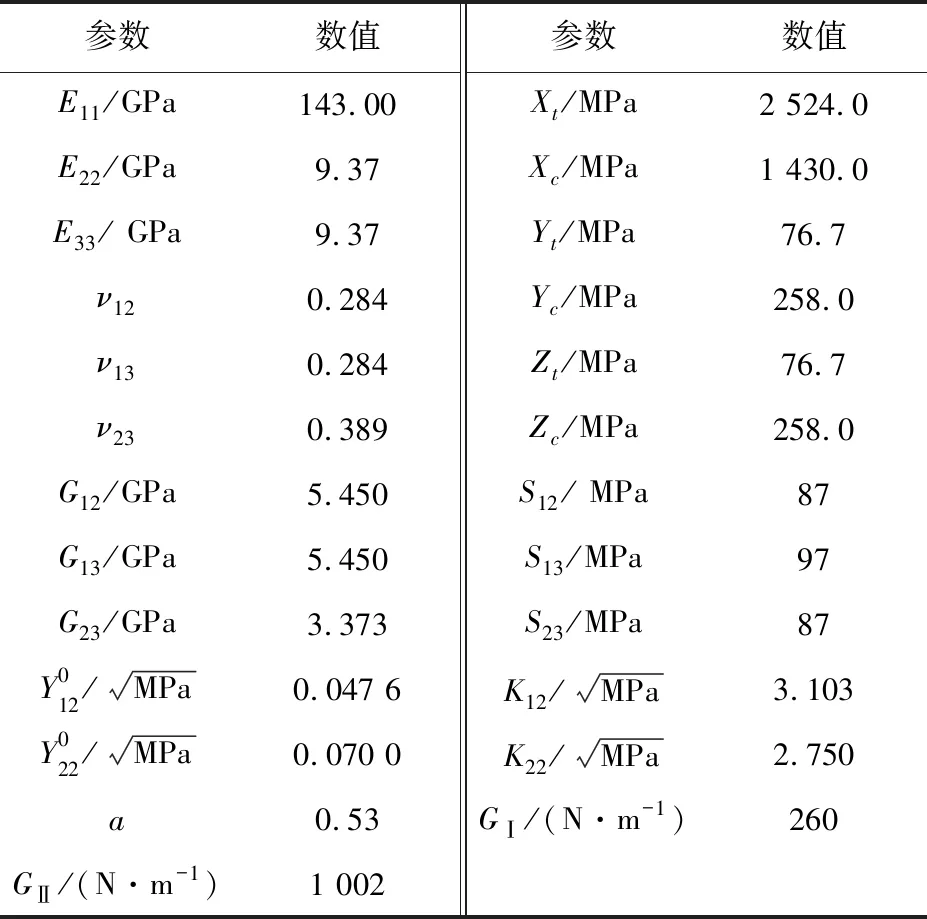
參數數值參數數值E11/GPa143.00Xt/MPa2 524.0E22/GPa9.37Xc/MPa1 430.0E33/ GPa9.37Yt/MPa76.7ν120.284Yc/MPa258.0ν130.284Zt/MPa76.7ν230.389Zc/MPa258.0G12/GPa5.450S12/ MPa87G13/GPa5.450S13/MPa97G23/GPa3.373S23/MPa87Y012/MPa0.047 6K12/MPa3.103Y022/MPa0.070 0K22/MPa2.750a0.53GⅠ/(N·m-1)260GⅡ/(N·m-1)1 002

2.2 開孔層合板有限元分析

有限元模型在ABAQUS/Standard中建立，為了保證模型的計算精度，對孔邊單元進行適當細化。模型的單元總數為18 752個，單元類型均采用8節點減縮積分單元C3D8R。

準各向同性鋪層ZT7H/5429復合材料開孔層合板數值模擬及試驗得到的應力-應變曲線如圖3所示，可以看出：兩條曲線在加載前半段保持一致，只在加載后半段才發生一定程度的分離，整體吻合情況良好；通過數值模擬獲得的開孔板極限強度為390.3 MPa，僅比試驗值高出0.86%；在達到極限載荷之前，該準各向同性開孔板在拉伸載荷下的應力-應變響應曲線基本呈線性關系，究其原因，對于單層而言，層合板中0°層在拉伸方向的剛度很強且呈現明顯的線性響應特征，而其他鋪層在拉伸狀態下的非線性特征相對而言卻并不明顯；同時，準各向同性開孔板中的0°層比例達到了25%，反映在層合板的宏觀應力應變響應上，較高比例0°層的線性響應會掩蓋其他鋪層的非線性響應。

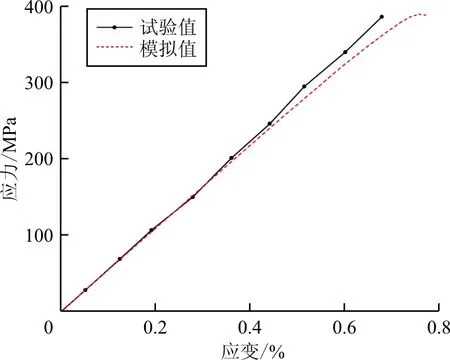
圖3 開孔板應力-應變曲線試驗值與數值模擬對比

數值模擬獲得的準各項同性開孔層合板在到達拉伸極限載荷時的基體損傷與纖維損傷狀況如圖4所示。

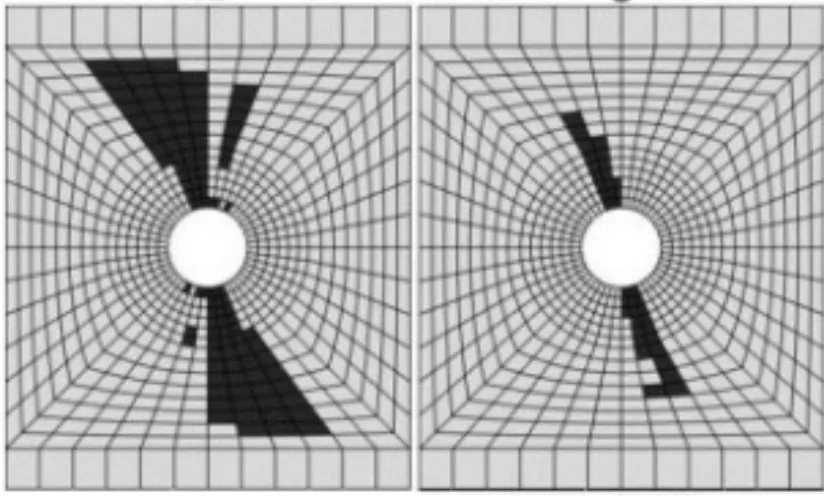
(a1) 45° (a2) 0°

(a3) -45° (a4) 90°

(a) 基體損傷(100%極限載荷)

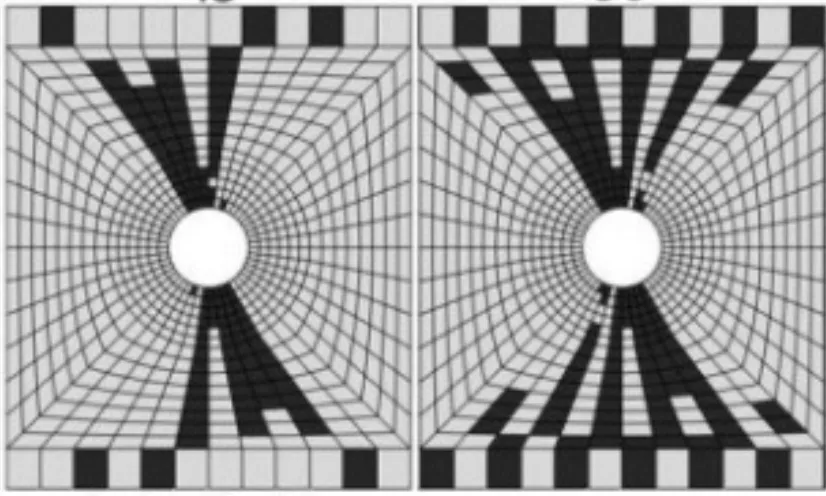
(b1) 45° (b2) 0°

(b3) -45° (b4) 90°

(b) 纖維損傷(100%極限載荷)

圖4 不同鋪層極限拉伸載荷下的基體與纖維損傷

Fig.4 Matrix damage and fiber damage of

different layers under ultimate tensile load

從圖4可以看出：在拉伸極限載荷時刻，對于基體損傷，90°層的范圍最大，±45°層的范圍次之，這些鋪層的損傷均接近或已擴展至板邊緣，0°層的損傷范圍最小，約擴展至半板寬的位置；而此時，90°層尚未發生纖維損傷，0°層與±45°層的纖維損傷程度十分接近，其范圍略大于半板寬。

基體損傷和纖維損傷的共同累積使得開孔板達到其最大承載能力，繼續加載將使結構中各層的損傷范圍都迅速朝著板邊緣擴展，最終導致開孔板完全斷裂，形成如圖5所示的斷裂形貌。

圖5 開孔層合板試驗件拉伸失效模式

綜上所述，本文采用的復合材料三維非線性本構可以較為準確地模擬含開孔層合板的應力應變響應及其損傷斷裂情況。因此，可將上述本構模型引入到復合材料螺栓連接結構拉伸強度預測與失效分析之中。

3 復合材料螺栓連接結構拉伸分析

3.1 螺栓連接結構拉伸試驗概況

復合材料螺栓連接結構類型為單釘雙搭接，搭接板材料均為ZT7H/5429，基本材料參數如表2所示，且三塊搭接板鋪層方式均為[45/-45/0/0/45/90/-45/0/45/0/-45/90/45/0/-45/0/45/0/-45/0]s。螺栓材料為Ti-6Al-4V鈦鋁合金，彈性模量為110 GPa，泊松比為0.29。在夾持區域，分別在中搭接板的上下兩側，以及上、下搭接板之間增加厚度為5 mm的鋁合金墊片。單釘雙搭接結構的幾何參數如圖6所示。試驗同樣在室溫條件下進行，參照ASTM-D5961標準,所用的加載設備、應變片、膠粘劑、應變采集系統均與2.1節一致，位移加載速率為1 mm/min。

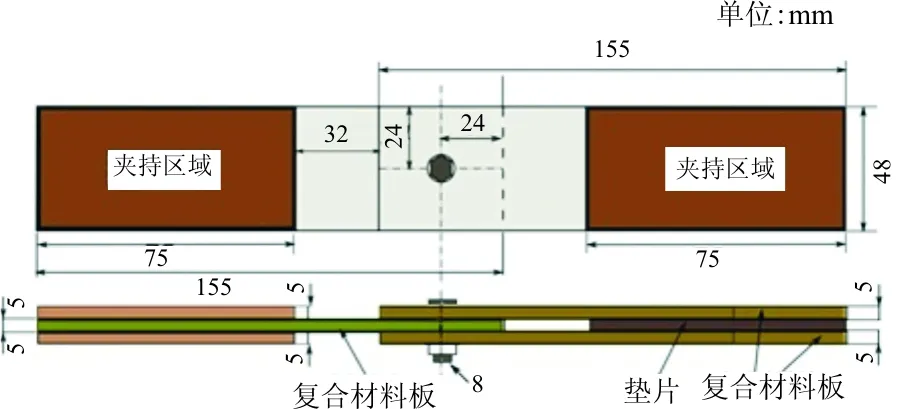
圖6 復合材料單釘雙搭接試件幾何示意圖

3.2 螺栓連接結構有限元分析

單釘雙搭接結構有限元模型如圖7所示，建模區域為試驗件非夾持段，上搭接板與下搭接板端部固支，中搭接板沿x軸負方向加載。上-中搭接板、中-下搭接板、螺栓-搭接板之間設置接觸，對應的摩擦系數分別為0.7、0.7和0.1。與開孔板相同，對各搭接板的孔邊區域進行單元細化，模型單元總數為107 280個，單元類型仍采用8節點減縮積分單元C3D8R；螺栓材料采用彈性本構。

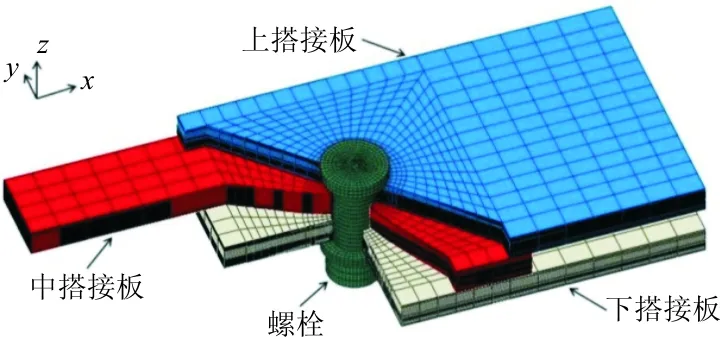
圖7 單釘雙搭接結構有限元模型示意圖

3.2.1 位移載荷響應

單釘雙搭接結構分別通過試驗和數值模擬獲得的載荷位移曲線如圖8所示，可以看出：試驗值與模擬值吻合良好，數值模擬得到的極限載荷為51.2 kN，試驗獲得的極限載荷為53.5 kN，誤差約為4.62%。

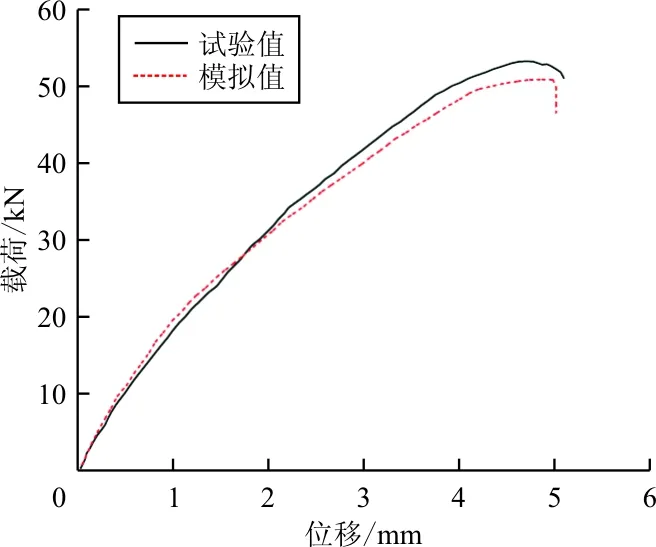
圖8 單釘雙搭接結構載荷位移曲線

3.2.2 失效分析

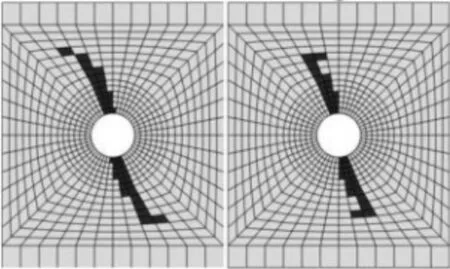
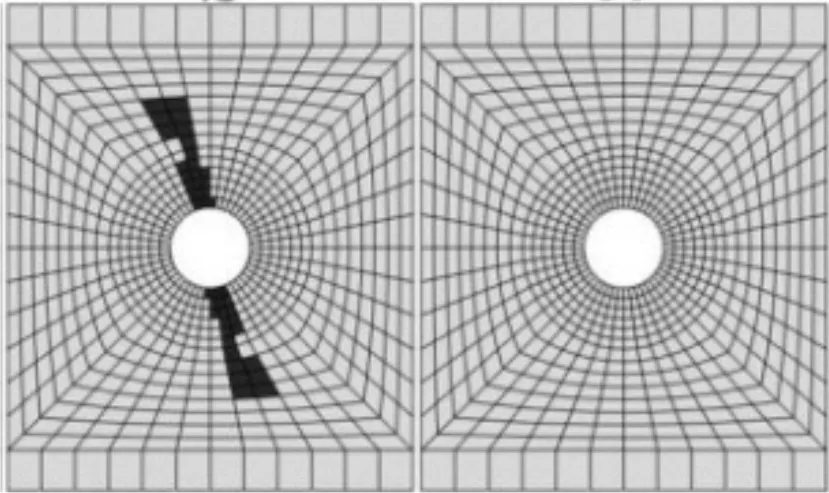
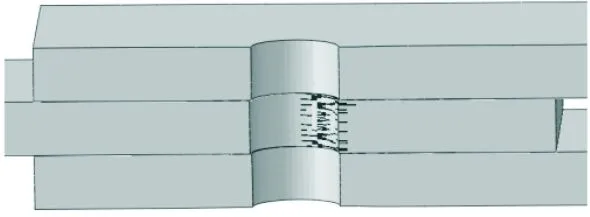
復合材料單釘雙搭接結構在承受拉伸載荷時，由于螺栓的擠壓作用，其內部損傷是一個不斷累積的過程，借助有限元分析結果，可對其進行具體分析。針對結構內部的纖維損傷演化情況進行說明，如圖9所示。

(a) 34%極限載荷

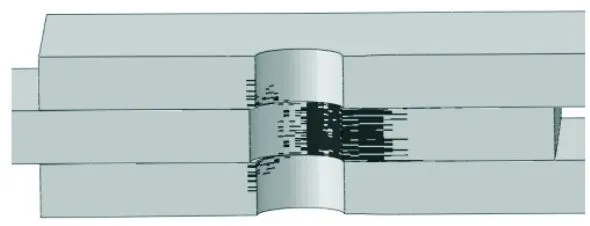
(b) 75%極限載荷

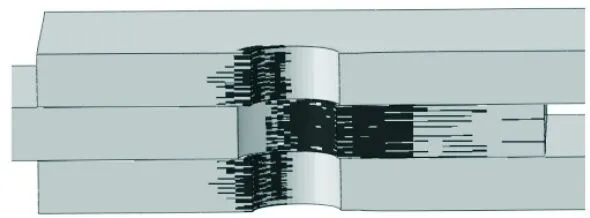
(c) 100%極限載荷

從圖9可以看出：當載荷達到17.4 kN(34%極限載荷)時，中搭接板的孔邊與螺栓接觸區域開始產生一定程度的纖維損傷，同時孔邊出現一定程度的擠壓變形，導致結構剛度開始出現下降，反映在位移載荷曲線上則是對應位置的斜率降低，且在隨后的加載過程中，結構剛度持續下降；而當載荷進一步增大到38.4 kN(75%極限載荷)時，上、下搭接板靠近中搭接板的位置產生初始纖維損傷，同時中搭接板纖維損傷范圍沿厚度方向和擠壓徑向也明顯擴大；隨著載荷繼續增大到結構的極限載荷，中搭接板的纖維損傷朝端部進一步擴展，而其孔邊與加載方向垂直的位置雖未與螺栓直接發生擠壓接觸，但由于該位置宏觀力學響應上受拉且存在明顯的應力集中效應，也產生了嚴重的纖維拉伸損傷，但損傷范圍僅限于靠近孔邊的區域，未沿著中搭接板橫向發生大范圍擴展；此時，上、下搭接板孔邊與螺栓接觸區域的纖維損傷也已擴展至整個層合板的厚度方向，但由于它們各自分別承受的擠壓載荷僅約為中搭接板擠壓載荷的一半，故二者的纖維損傷只產生在孔邊附近位置，未沿擠壓徑向大范圍擴展。

損傷在中搭接板內部的大范圍累積導致結構失去進一步承受更高載荷的能力，繼續加載將使得結構的損傷迅速擴展，中搭接板最終破壞模式為擠壓失效，與試驗觀察結果(如圖10所示)一致。

圖10 單釘雙搭接試件中搭接板擠壓失效

4 結 論

(1) 采用Hashin失效準則、能量耗散率方法、Puck失效準則和材料損傷連續退化方法相結合的復合材料非線性三維本構模型可有效模擬開孔板及螺栓連接結構在拉伸載荷作用下的力學響應，且計算收斂性良好。

(2) 在計算開孔板和螺栓連接結構的極限拉伸強度時，二者的有限元數值模擬結果與試驗值之間的誤差分別為0.86%和4.62%，均滿足工程計算精度要求。

(3) 對于復合材料單釘雙搭接螺栓連接結構，隨著拉伸載荷的增大，搭接板的損傷累積和孔邊擠壓變形導致其位移載荷響應呈非線性特征且剛度逐漸降低。加載過程中，中搭接板的損傷最先萌生，且其損傷程度也最為嚴重，損傷在其內部的大范圍擴展使得連接結構達到承載極限，在最終破壞模式上則表現為中搭接板的擠壓失效。