基于時頻切片分解的時變系統參數識別
陳淇,史治宇,張杰
(南京航空航天大學 機械結構力學及控制國家重點實驗室,南京 210016)
0 引 言
系統的時變問題指的是,因外部環境影響或自身結構特性,系統的動力學參數隨時間變化的問題。隨著人類社會的進步和科學技術的發展,工程結構的時變問題在包括土木工程、機械設計、航空航天等多個領域日漸突出。例如,高超聲速飛行器在高速飛行過程中,因自身的氣動布局和氣動加熱等問題導致的顫振現象[1];汽車經過橋梁時,因為附加質量導致的車橋系統集中質量隨汽車位置而改變;人工智能機械手臂在旋轉過程中,因結構本身的改變,而導致的空間質量分布和剛度分布的改變等。因此,時變系統參數識別方法的研究有著重要的學術價值和工程價值。
為了尋找到一種可靠的時變系統參數識別方法,國內外學者做過諸多努力。20世紀80年代,A.Grosssman等[2]為了研究地震波的時頻特性首次提出了小波的概念;而后,W.J.Staszewski等[3]基于小波的各種改進方法被用于動力學參數識別領域。許鑫等[4]在連續小波積分的基礎上,把振動微分方程轉化為以加速度項表達的小波變換式,并提出了基于加速度響應的連續小波變換的時變系統參數識別方法。N.E.Huang等[5-6]提出了經驗模態分解法(即EMD法),該方法與M.Feldman[7-8]的Hilbert變換相結合,便是著名的Hilbert-Huang變換(HHT變換),可用以識別時變系統參數。1997年,K.Liu[9]在狀態子空間模型的基礎上,引入了自由響應時變系統參數識別,并于兩年后將該方法推廣至受迫響應下的時變系統參數識別。狀態空間的方法后續還經歷了諸多發展[10],例如龐世偉等[11-12]引入的投影估計法、M.Raffy等[13]對漸進性統計誤差的估計等。這些改進的方法都對狀態空間方法的研究與發展做出了重要貢獻。
上述識別方法在不同層面上均有一定的局限性。因為涉及小波基函數的選取,所以小波的方法需要有一定的信號先驗信息,是非自適應的。而HHT變換盡管對所有信號都具有自適應性,但其本身是一種經驗式的信號分解方法,存在模態混疊、缺乏正交性證明等缺陷[14]。狀態空間的方法涉及矩陣計算,存在計算量大等問題。
在吸取了短時傅里葉變換和連續小波變換的優點下,Yan Zhonghong等[15]提出了頻率切片小波變換的方法;鐘先友等[16-17]將其用于處理爆破分析和故障診斷等信號分析方面的問題。本文則吸取切片小波基可在任意時頻區間對信號進行切片的優點,提出基于時頻切片分解的時變系統參數識別方法,用以識別時變系統隨時間而變化的模態參數。
1 理論介紹
1.1 時變振動系統基本理論
假設系統為n自由度的時變系統,在第k個自由度上受到脈沖激勵作用,則系統的振動微分方程為[18]
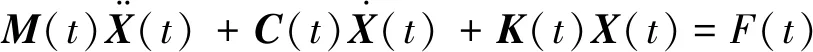
(1)
式中:F(t)為系統所受到的第k個自由度上的脈沖激勵;M(t)、C(t)和K(t)分別為系統質量矩陣、阻尼矩陣、剛度矩陣,它們的數值都隨著時間而改變。
設阻尼為比例阻尼,則可引入X(t)=Φ(t)q(t)對系統進行模態解耦,Φ(t)=[φ1(t),φ2(t),…,φn(t)],為固有陣型矩陣;q(t)=[q1(t),q2(t),…,qn(t)]T,為模態坐標矩陣。解耦結果為
(2)

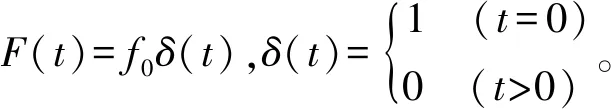
(3)
根據模態疊加法,第p自由度上的系統位移響應xp(t)為各階模態位移響應xpj(t)的疊加,即
(4)
xpj(t) =φpj(t)qj(t)
=Bpj,k(t)e-ζj(t)ωj(t)t×
(5)
1.2 切片小波基及其相關理論
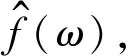
(6)
那么,可以利用切片小波基函數對f(t)進行時頻變換[8],變換結果為
(7)
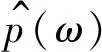
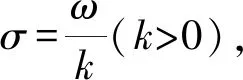
(8)
式中:k為與ω、u獨立的變量,定義為時頻分辨系數,用以表征時頻切片窗的時頻伸縮尺度。
根據海森堡測不準原理,時頻切片窗口的頻率邊長和時間邊長的乘積為一常數,相對精準的時間分辨率將以犧牲頻率分辨率為代價,相對精準的頻率分辨率將以犧牲時間分辨率為代價,而時頻分辨系數k的數值將決定時頻分解對頻率或時間的敏感度。
對于時頻分解的結果,可利用逆變換進行信號還原,得到原信號在任意時間區間和任意頻率區間內的重構信號,對于時間切片區間(t1,t2)和頻率切片區間(ω1,ω2),重構信號的表達式為
(9)
綜上,利用切片小波基可在任意時頻區間對信號進行切片和其逆變換重構還原快速便捷的特點,本文引入針對時變系統的時頻切片分解參數識別方法。
1.3 基于時頻切片的時變系統參數識別
由時變系統基本理論可知,n自由度的時變系統脈沖激勵下第k自由度上的響應激勵可表示為n個單模態信號的線性疊加,而這n個單模態信號中分別包含了系統的n階模態信息。因此,時變響應信號的識別是解決時變問題的關鍵。傳統的EMD方法利用經驗模態分解算法處理響應信號,經驗式地將響應信號分解為多個本征模態函數進行識別,盡管有較好的自適應性,卻存在本征模態函數正交性難以證明等問題。本文則引入時頻切片分解的方法來解決響應信號的識別問題,具體時頻切片分解和后續識別過程如下:
對振動系統采集到的第p自由度上的時變位移響應xp(t),選擇合適的切片小波進行整個時間域的時頻分解,可得到其時頻分布能量圖,再根據信號的時頻分布特性,劃分出n個時間頻率區間,接著依據這n個時間頻率區間分別對位移響應xp(t)進行時頻分解,得到n個獨立的時頻分解后的信號,分解出的這n個信號即為組成系統脈沖激勵響應的n個單模態信號。
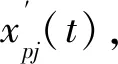
(10)
式中:r(t)為時頻切片分解的殘差項。
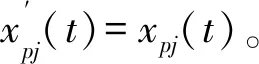
(11)
式中:Apj(t)為解析信號的幅值函數;φpj(t)為解析信號的相位函數。
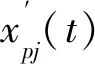
(12)
進一步可得:
(13)
則解析信號幅值圖InApj(t)-t的斜率為單階模態頻率和阻尼比乘積的相反數-ζjωj,解析信號相位圖φpj(t)-t的斜率為單階模態阻尼頻率ωdj。
基于時頻切片分解的時變系統參數識別方法流程圖如圖1所示。
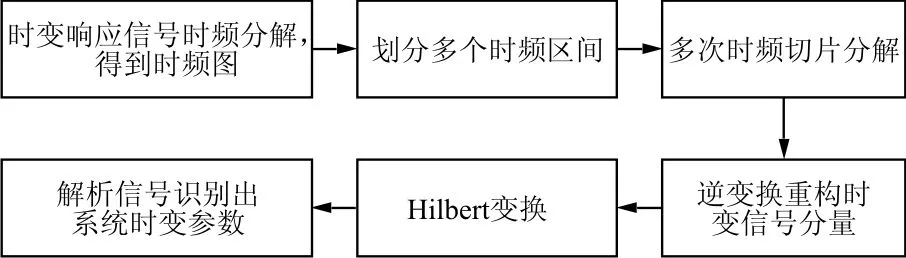
圖1 基于時頻切片分解的時變系統參數識別方法流程圖
2 仿真分析
為了更直觀地展現基于時頻切片的時變系統參數識別方法,設計一個三自由度的彈簧—阻尼—質量塊結構仿真實驗,如圖2所示。
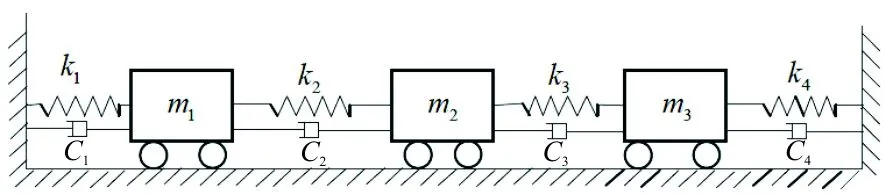
圖2 仿真結構示意圖
初始位移、速度、加速皆為0,結構初始參數為
結構參數隨時間而變化,變化規律為
(14)
激勵為脈沖激勵,作用在質量塊3(m3)上,使用Newmarkβ算法計算10 s內結構各個自由度上的位移響應。選取第二個自由度上的位移響應進行時頻切片分解,得到時頻分布圖如圖3所示。

圖3 位移響應信號的時頻分布能量圖
從圖3可以看出:信號中主要包含了三階能量分量,按照自然頻率段5~13、13~20、25~35 Hz劃分出三個頻率切片段,時間切片長度皆為10 s;這三個切片片段再次對響應信號分別進行三次時頻切片分解,得到三段獨立的時頻信號,如果以時頻圖來展示這三段信號,將得到與圖3類似的三幅各自頻率段上的時頻,故本文不再重復展示。
對于時頻切片分解的結果,即三段獨立的時頻信號,分別通過逆變換算法進行信號重構,得到三段時域上的重構信號,也就是三階單模態時域信號,如圖4所示。
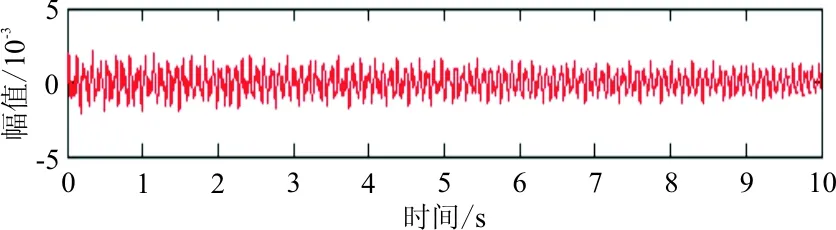
(a) 原信號
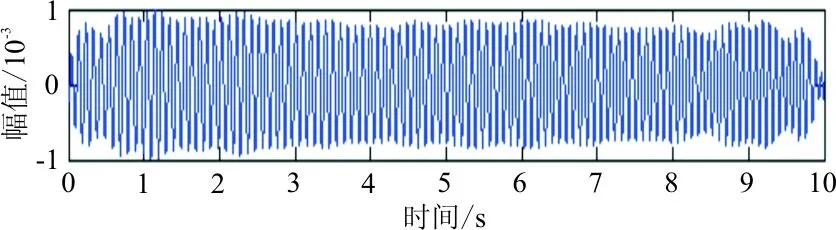
(b) 切片1信號重構

(c) 切片2信號重構
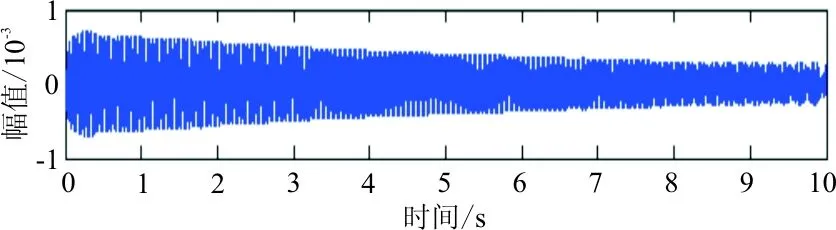
(d) 切片3信號重構
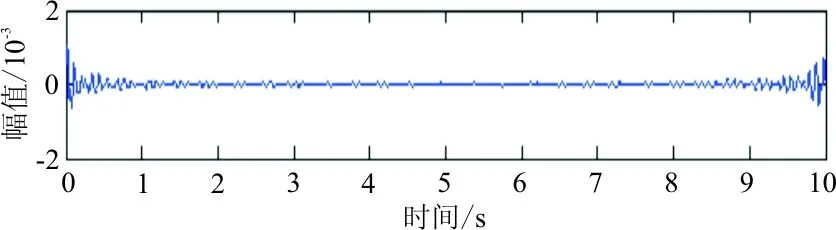
(e) 殘差信號
從圖4可以看出:響應能量在時間區域上分布較均勻,第一階能量較強,第二、第三階能量相對弱些,但和第一階能量大致在數量級上不存在差異,表明本次仿真包括參數設置、激勵點/響應點位置選取、激勵方式的選擇都較為合理,比較完整地激發出了結構的三階能量信息。殘差信號為原信號減去重構分量信號所得。
對于重構的分量信號,依次進行Hilbert變換識別系統各個時間上的阻尼頻率,以圓頻率形式表示,并和理論計算的阻尼頻率相比較,如圖5~圖7所示。
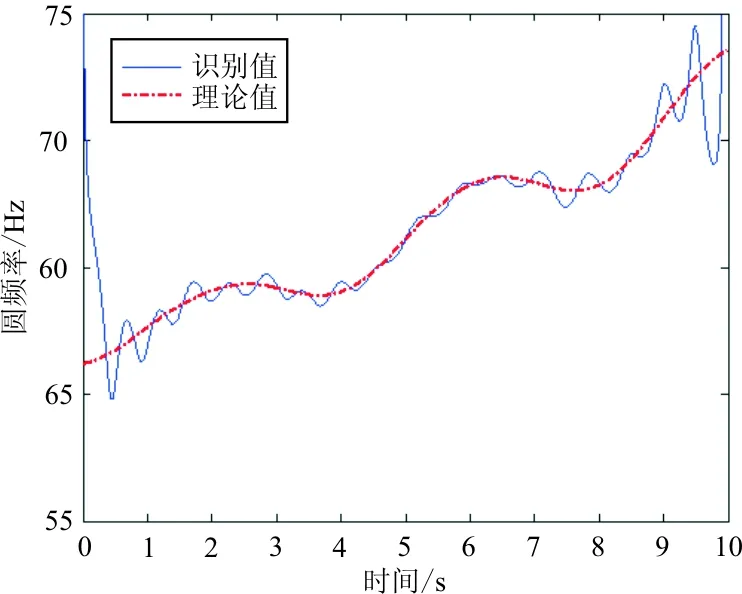
圖5 第一階阻尼頻率識別值和理論值對比圖
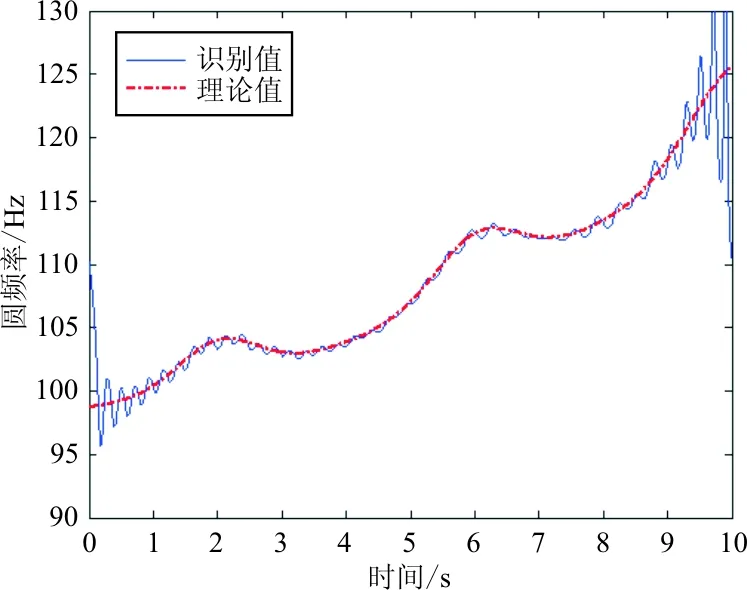
圖6 第二階阻尼頻率識別值和理論值對比圖
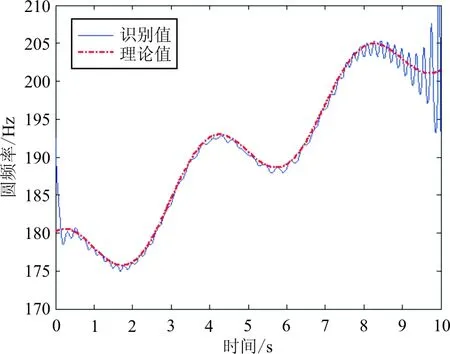
圖7 第三階阻尼頻率識別值和理論值對比圖
從圖5~圖7可以看出:除了無法避免的邊界效應外,識別出的三階阻尼頻率和理論三階阻尼頻率隨時間變換趨勢一致,數值基本重合。
為了進一步展示識別誤差,使用平均相對百分比誤差MAPE,計算公式為
(14)
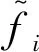
本文識別出的一階、二階和三階模態阻尼比的MAPE分別為1.080%、0.740%和0.043%。考慮到不可避免的邊界效應造成的誤差在MAPE計算中的占比并不小,因此該識別方法在大部分時間域中的誤差水平要比MAPE展示的誤差水平還要低得多。可以認為基于時頻切片分解的時變系統參數識別方法擁有非常好的識別精度和實用價值。
3 結 論
(1) 基于時頻切片分解的時變系統參數識別方法可以將多自由度時變系統的響應信號進行切片分解,將原本的位移響應信號分解為多個單模態信號。再經過逆變換完成時域上的重構,對于重構后的各階信號,通過Hilbert變換提取信號瞬時頻率,從而識別出時變結構的各階頻率。
(2) 該方法時頻切片分解的逆變換算法不依賴于切片小波基的選取,使得信號逆變換非常方便快捷,相較于傳統的小波方法,具有計算效率高的優點。
(3) 盡管信號經過多次切片小波分解,但是每次切片分解和重構過程都是獨立進行的,各階誤差不會相互影響,故抗噪能力強。
(4) 端點處的誤差是小波類方法通有的端點效應造成的,可以通過延長采樣時間,讓端點效應產生在一個不關心的時間區域中來解決。
(5) 仿真算例展示了時頻切片分解的時變系統參數識別方法的具體步驟和效果,驗證了其可行性,表明其識別精度高。

